
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решения в условиях неопределенности состояния окружающей средыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Принятие решений в условиях риска. Ситуация риска возникает тогда, когда с каждой принимаемой стратегией x Î X связано целое множество возможных результатов s 1, s 2, …, sn с известными вероятностями p (x, s), s Î S ={ s 1, s 2, …, sn }. Полезность этого исхода запишем как u (x, s),.Ожидаемую полезность от выбора значения x (от выбора стратегии x) можно записать
Задача принятия решения будет иметь вид Принятие решений в условиях неопределенности Будем считать, что в исследуемой операции множество X конечное, т.е. X ={ x 1, x 2, …, xm }, внешняя среда (природа), которая может находиться в одном из состояний s Î S ={ s 1, …, sn }известных ЛПР, но больше ни каких характеристик по исходу этих состояний нет. Как и выше, полезность исхода запишем как u (x, s). Так как множества X, S конечные, то задачу принятия решения обычно записывают в виде следующей матрицы U размерностью т ´ п, I – индекс переменной x Î{ x 1, x 2, …, xm }, j – индекс переменной s Î{ s 1, s 2, …, sn },
В условиях неопределенности считается, что наблюдателю неизвестно распределение вероятностей p (x, s). Относительно состояния среды наблюдатель может высказать определенные гипотезы. Его предположения о вероятном состоянии среды называются субъективными вероятностями. Этот недостаток информации обусловил развитие следующих критериев для анализа ситуации, связанной с принятием решения: 1. Критерий Вальда 2. Критерий Гурвица 3. Критерий Лапласа. 4. Критерии Сэвиджа. Эти критерии отличаются по степени консерватизма, который проявляет индивидуум, принимающий решение, перед лицом неопределенности. Критерий Вальда (критерий осторожного наблюдателя). Этот критерий оптимизирует полезность в предположении, что среда находится в самом невыгодном для наблюдателя состоянии. По данному критерию решающее правило имеет следующий вид:
По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния среды. Критерий Гурвица Рассмотрим два предположения: среда может находиться в самом невыгодном состоянии с вероятностью (1 – a) и самом выгодном — с вероятностью a, где a коэффициент доверия, 0 ≤ a ≤ 1. Решающее правило записывается так:
Если a = 0, получаем критерий Вальда. Если a = 1, то приходим к решающему правилу вида:
Это так называемая стратегия «здорового оптимиста», который верит в удачу.
Критерий Лапласа. Состояния среды считают равновероятными p (S 1)= p (S 2)= … = p (Sn)=1/ n. В результате решающее правило определяется соотношением
Критерий Сэвиджа (критерий минимизации «сожалений»). «Сожаление» — это величина, равная изменению полезности результата при данном состоянии среды относительно наилучшего возможного состояния. Чтобы определить «сожаление», поступают следующим образом. В исходной матрице
Искомую стратегию x Î{ x 1, x 2, …, xm }, которая минимизирует «сожаление», определяют из условия
Этот критерий минимизирует возможные потери при условии, что состояние среды наихудшим образом отличается от предполагаемого. Пример. Некоторая фирма решает построить отель в одном из курортных мест. Необходимо определить наиболее целесообразное количество мест или комнат в этой гостинице. Составляют смету расходов по строительству гостиницы с различным количеством комнат, а также рассчитывают ожидаемый доход в зависимости от количества комнат, которые будут сняты. В зависимости от принятого решения — количества комнат в гостинице x =20, 30, 40, 50 и количества снятых комнат S =0, 10, 20, 30, 40, 50, которое зависит от множества случайных факторов и неизвестно фирме, получают следующую таблицу ежегодных прибылей: Таблица 1. 2
Определим наиболее подходящее количество комнат в гостинице по выше приведенным критериям. Критерий Вальда.
Судя по результатам, критерий Вальда не применим, так как в этом случае от постройки гостиницы следует отказаться. Критерий Лапласа. Приведем таблицу вычислений по этому критерию
xопт = x 3=40. Критерий Гурвица. Таблицы вычислений по критерию Гурвица будут иметь вид:
Выделенные клетки соответствуют максимуму в столбце. Тогда оптимальное количество комнат в гостинице в зависимости от a
Критерий Сэвиджа. В каждом столбце найдем максимальное значение, получим:
Матрица сожалений примет вид:
Выбирая из нее Таким образом: по критерию Вальда строить 20 комнат; по критерию Лапласа строить 40 комнат; по критерию Гурвица строить 20 комнат, если заказчик – пессимист и 50 комнат, если заказчик оптимист; по критерию Сэвиджа 40 комнат. Какое из возможных решений предпочтительнее? Это определяется выбором соответствующего критерия (Вальда, Лапласа, Гурвица или Сэвиджа).
Самостоятельная работа №2 1). При освоении новой территории предполагается построение поселка, в котором должна быть построена школа. Переменные a 1 ÷ a 4представляют возможные ее размеры (на 200, 250, 300, 350 человек), а переменные s 1 ÷ s 5 соответствуют возможному числу ее участников (0, 200, 250, 300, 350 человек). Следующая таблица содержит матрицу стоимостей (в условных единицах), описывающих затраты в случаях, если если размеры школы ai , число учеников sj.
Проанализировать описанную ситуацию с точки зрения четырёх рассмотренных выше критериев. 2) Cтудент, который обычно получает хорошие отметки, благодаря тому, что имеет возможность повторить материал в ночь перед экзаменом, столкнулся с небольшой проблемой. Его сокурсники организовали на всю ночь вечеринку, в которой он не хочет участвовать. Имеет три альтернативы: а1 – участвовать в вечеринке всю ночь, а2 – половину ночи участвовать в вечеринке, а половину – учиться, а3 – учить всю ночь. Профессор, принимающий завтрашний экзамен, непредсказуем, в том смысле, что экзамен может быть легким (s 1), средним (s 2) или трудным (s 3). В зависимости от сложности экзамена и времени, затраченного на повторение, можно ожидать следующие экзаменационные балы
Порекомендуйте, какой выбор он должен сделать этот студент Варианты заданий.
3. Задачи выпуклого векторного программирования [1]. Задача выпуклого программирования заключается в отыскании минимального значения функционала (критерия) при некоторых ограничениях: j 0(x)®min, x Î XÍRn где j 0(x) – выпуклая функция, X – выпуклое множестмо. Задача выпуклого векторного (многокритериального) программирования запишем в виде
где M также конечное индексное множество, если это множество одноэлементное, то получаем задачу выпуклого программирования, в противном случае задачу выпуклого векторного программирования. Для многокритериальных задач необходимо всегда определить, что понимается под оптимальным решением. В данном случае под оптимальностью мы будем понимать оптимальность по Парето и Слейтеру, определения которых будут даны ниже [Подиновский,Акоф, Моудера ]. Широко бытует мнение, что многокритериальные задачи принципиально отличаются от однокритериальных задач. Возможно, что с точки зрения процедуры принятия решения это и так, например, множества точек, оптимальных по Слейтеру (или Парето) часто представляют собой замкнутые области, а требуется выбрать только одно решение. Однако с точки зрения математического аппарата, аппарат многокритериальных задач рассматриваемого класса незначительно отличается от аппарата однокритериальных. Это подтверждают работы [Коваленко А.Г. Элементы]. Ниже рассмотрены основные понятия, используемые при решении задачи выпуклого векторного программирования.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.35.129 (0.01 с.) |

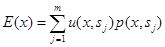 . (1. 4)
. (1. 4) .
.
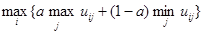
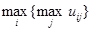 .
.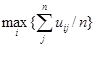
 в каждом столбце находят максимальный элемент
в каждом столбце находят максимальный элемент  . Из него вычитают элементы этого столбца, получая матрицу «сожалений»
. Из него вычитают элементы этого столбца, получая матрицу «сожалений»

 , отсюда i =1, xопт = x 1=20.
, отсюда i =1, xопт = x 1=20.



