
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет потенциалов и проверка критерия оптимальности, переход к новому базисуСодержание книги
Поиск на нашем сайте
Для базисных переменных должно выполняться vj:= ui+cij. Положим u 1=0, тогда по этой формуле по клетке (1,2) v 2=0+2=2, по клетке (1,2) v 2=0+7=7. Из клетки (2,2) u 2=7–4=3. Продолжая аналогичным образом, получим информацию, приведенную в следующей таблице
Подсчитываем значения dij по формуле dij = vj–ui–cij и заносим в таблицу. Для базисных клеток dij =0. В клетке (1,4) dij >0, поэтому включаем эту клетку в базис, но нам нужно определить клетку, выходящую из базиса. Выполним это на следующей таблице, в ней клетка (1,4) затемнена. Легко видеть, что затемненные клетки образуют цикл (1,4)Þ(3,4)Þ(3,3)Þ(2,3)Þ(2,2,)Þ(1,2)Þ(1,4)
Заносим в позицию q клетки значения «+» и «–». В каждой строке и в каждом столбце их должно быть ровно по одному значению. Начинаем с клетки (1,4), далее идет чередование. В соответствии с этим, положим x 1,4= x 1,4+ Q, x 3,4= x 3,4– Q, x 3,3= x 3,3+ Q, x 2,3= x 2,3– Q, x 2,2= x 2,2+ Q, x 1,2= x 1,2– Q. Увеличиваем значение от нуля до значения, когда одна из этих переменных обратится в 0, это будет при Q =min(x 34, x 23, x 12)=1. Этот минимум достигается на клетке (1,2), поэтому она исключается из базиса (если минимум достигнут на нескольких клетках, то исключается из базиса только одна). Выполним преобразования и данные внесем в таблицу
Значение функционала на этом решении будет равно
F =2´10+4´1+4´16+3´1+3´13+7´11=191. Этот алгоритм повторяем до тех пор, пока не окажется, что все значения dij £0. Оптимальным решением будут значения xij последней таблицы. Самостоятельная работа 14. Решить транспортную задачу при m =3, n =4. Значения векторов a и b, матрицы С взять из таблицы в соответствии с номером варианта:
Динамическое программирование и потоки в сетях
Динамическое програмиирование возникло и сформировалось в пятидесятых годах прошлого столетия благодаря работам Беллмана и его сотрудников. Первые задачи, которые привели к появлению вычислительного метода динамического программирования, являлись динамическими задачами управления запасами. Сущность вычислительного метода динамического программирования рассмотрена в представленных в данной главе лабораторных работах. Задача оптимизации многошаговых процессов, задача о ранце. Задача оптимизации многошаговых процессов имеет вид
Обозначим через Wi (xi) максимум в следующей задаче:
Справедливо следующее функциональное соотношение Беллмана:
Для того, чтобы решение ((xi) i =0,1,2,..., n , (ui) i =1,2,3,..., n ),удовлетворяющее ограничениям (7.1) – (7.5) было оптимальным, необходимо и достаточно, чтобы
Таким образом, получаем следующий алгоритм решения оптимизации многошаговых процессов. Алгоритм. Первый этап. 1. Для всех x Î Xn положить Wn (x)=0; 2. Последовательно для i = n –1, n –2, n –3,…,0 выполнить: для всех x Î Xi положить:
Второй этап. 1. Положить x 0:= a 0; 2. Последовательно для i =1, 2,3,…, n положить:
Полученное в результате работы алгоритма решение ((xi) i =0,1,2,..., n , (ui) i =1,2,3,..., n )будет оптимальным для задачи (7.1) – (7.5). Оптимальное значение функционала будет равно W 0(a 0).
Задача о ранце имеет вид
где ui– целые числа i =1,2,3,..., n. Числа ai также будем рассматривать целыми, i =1,2,3,..., n. Введем переменные x 0=0,
Задача (7.8) – (7.12) имеет такой же вид, как и задача (7.1) – (7.5), поэтому для ее решения можно применить алгоритм, описанный выше. Легко показать, что для задачи о ранце
Соотношение Беллмана примет вид
где [ a ] – целая часть числа a. Пример. Решить задачу:
В этой задаче n =2, b =3, поэтому таблица с результатами вычислений будет иметь вид:
Приведем пояснения к заполнению этой таблицы в соответствии с выполнением алгоритма. Первый этап. Заполнение столбца W 2 понятно, оно соответствует выполнению пункта 1 первого этапа алгоритма. Покажем, как заполнялась клетка (x, i)=(0,1). Ее заполнение соответствует вычислению
для x =0, i =0,
или
В соответствии с этим,
Аналогично получены все остальные элементы этого столбца. Покажем вычисления для клетки (0,0). Для нее
При u =0 При u =1 Таким образом, W 0(0)=6, u 1(0)=0. Остальные клетки столбца 0 не заполняем, так как X 0={0}. Второй этап. 1. x 0=0. (в следующей таблице клетка (0,0) выделена) 2. u 1= u 1(x 0)= u 1(0)=0, x 1= x 0+2´ u 1=0 (клетка (0,1) выделена) 3. u 2= u 2(x 1)= u 2(0)=3, x 2= x 1+1´ u 2=3 (клетка (3,2) выделена)
Ответ. Максимальное значение функционала в задаче равно 6, u 1=0, u 2=3. Самостоятельная работа 15. Решить задачу о ранце при n =5, b =8, значения c (i), a (i), i= 1,2,3,..., n,взять из следующей таблицы в соответствии с номером варианта.
Результаты представить ввиде таблицы
Выписать оптимальное значение функционала и значения переменных, на которых он достигается.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.1.159 (0.009 с.) |



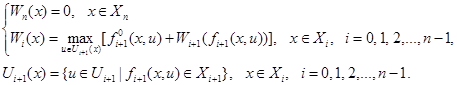





 . Из задачи (7.6) – (7.7) получим эквивалентную задачу
. Из задачи (7.6) – (7.7) получим эквивалентную задачу ,
,





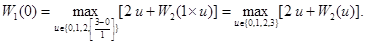
 Так как W 2(x)º0 (см. таблицу), то
Так как W 2(x)º0 (см. таблицу), то

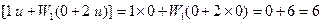 ,
, ,
,


