
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимосвязь равновесий по Нешу и Парето в играх.Содержание книги
Поиск на нашем сайте
Для начала рассмотрим широко известную игру Аумана. Суть ее заключается в следующем. Количество субъектов игры трое: банкир, и двое играющих. Банкир каждому игроку выдает деньги, в зависимости от того, какую стратегию выберет игрок. У каждого из них по две стратегии: A – отдай деньги мне; B – отдай деньги другому. При выборе стратегии A банкир выдает ему один доллар, при выборе стратегии B банкир отдает другому 100 долларов. В результате таблица выигрышей будет иметь вид:
Из таблицы ясно, что состояние равновесия по Нешу будет иметь вид (Отдай мне,Отдай мне). Из таблицы также видно, что объединившись в коалицию, игроки могут получить большие суммы. Предположим, что они это сделали и решили отбраковать те стратегии, которые одновременно не выгодны им обоим. Таковой является клетка (Отдай мне,Отдай мне), так как Мы не поднимаем вопроса о дележе, так как он не определен и зависит от неизвестных нам параметров. Но проведем анализ на устойчивость решения. (Отдай другому, Отдай другому). Предположим, что 1 игрок видя, что может получить больший выигрыш, решит нарушить правила коалиции и выберет стратегию Отдай мне. Второй игрок, обнаружив, что его выигрыш составит 0, также выберет стратегию Отдай мне. В результате игра вновь придет в состояние равновесия по Нэшу (Отдай мне,Отдай мне). Отметим, что состояние равновесия по Нэшу является устойчивым, так как заложено в самом определении этого понятия. Самостоятельная работа № 8. Найти все состояния равновесия по Парето в играх лабораторной работы 7, сравнить эти состояния с получившимися состояниями в предыдущей лабораторной работе.
Динамические игры с полной информацией Динамической игрой будем называть такую игру, в которой каждый игрок может сделать несколько ходов, и, по крайней мере, один из игроков, делая ход, знает, какой ход сделал другой игрок (возможно, он сам). В этой ситуации он стоит перед свершившимися фактами (уже сделанными ранее и известными ему ходами) и должен учитывать их при выборе своих действий. Рассмотрим пример динамической игры, под названием «Террорист». Игра «Террорист». В самолет, который должен лететь изМайами в Нью–Йорк, сел террорист. Террорист требует, чтобы пилот летел на Кубу, угрожая в противном случае взорвать самолет. Предположим, что террорист не может определить, куда действительно летит самолет. Первый ход в этой игре тогда делает пилот. Он может лететь либо на Кубу, либо в Нью–Йорк. Если пилот посадит самолет на Кубе, то еговыигрыш составит –1, а выигрыш террориста составит 1. Если же самолет сядет в Нью–Йорке, то делает свойход террорист. Он может либо взорвать бомбу, либо не взрывать. Если бомба взорвется, то выигрыши обоих игроков составят –100, в противном случае выигрыш пилота составит 1, а выигрыш террориста составит –1. Данную игру удобно представить в виде диаграммы, изображающей дерево игры.
Для отыскания решение игры в предположении, что игроки рациональны, их рациональность и структура игры известны обоим игрокам, можно воспользоваться методом обратной индукции. Шаг 1. Найдем вершину дерева, в которой выигрыши игроков неизвестны, но известны выигрыши на следующем уровне. Для данной игры это вершина «Нью–Йорк». На этом шаге выбор стратегии осуществляет террорист, он выбирает «не взрывывать». Тогда диаграмма игры принимает вид.
Шаг 2. Выполняется аналогично шагу 1, с той лишь разницей, что вершиной анализа является «Самолет в Майами», и ситуацию анализирует пилот. Поэтому диаграмма игры примет вид.
В ней выигрыш пилота составит +1, выигрыш террориста (–1), диаграмм решения будет иметь вид
Самостоятельная работа № 9 Задание 1. Муж и жена выбирают провести вечер дома или у друзей, причем, друзья у них разные. Выигрыши заданы следующей матрицей. Жена делает свой выбор первой. Проведут ли супруги вечер дома вместе? Объяснить почему? Муж делает свой выбор первым. Проведут ли супруги вечер дома вместе? Также объяснить почему?
Таблица вариантов приведена ниже:
Задание 2. 1. Решить антагонистическую игру (найти состояние равновесия), приведенную в матрицах:
2. Найти решений игры, состоящей из 2 ходов с полной информацией при условии, что игрок 1 делает ход первым. 3. Найти решений игры, состоящей из 2 ходов с полной информацией при условии, что игрок 2 делает ход первым. Провести анализ, сравнить получившие решения.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.56 (0.007 с.) |

 , т.е. клетка (Отдай другому, Отдай другому) предпочтительнее клетки (Отдай мне,Отдай мне) (напомним, что критерии в примере максимизируемые, поэтому понятие предпочтения имеет противоположный смысл, в отличии от введенного понятия предпочтения в разделе 2.). Для всех остальных клеток более предпочтительных нет, поэтому они являются оптимальными по Парето. Скорее всего, игроки примут совместное решение (Отдай другому, Отдай другому), так как суммарный выигрыш в нем наибольший.
, т.е. клетка (Отдай другому, Отдай другому) предпочтительнее клетки (Отдай мне,Отдай мне) (напомним, что критерии в примере максимизируемые, поэтому понятие предпочтения имеет противоположный смысл, в отличии от введенного понятия предпочтения в разделе 2.). Для всех остальных клеток более предпочтительных нет, поэтому они являются оптимальными по Парето. Скорее всего, игроки примут совместное решение (Отдай другому, Отдай другому), так как суммарный выигрыш в нем наибольший.



 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,
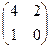 ,
,
 ,.
,.
 ,
,
 ,
,
 ,
,
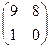 ,
,
 ,
,
 ,
,
 ,
,



