
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комбинаторные методы решения задач целочисленного линейного программирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Комбинаторные методы решения задач дискретного программирования основаны на полном переборе, в котором включены правила оценивания и отбраковки целых подмножеств решений, заведомо не содержащих оптимального решения. Классическая схема этого метода называется метод ветвей и границ. Общая схема метода ветвей и границ. Рассмотрим вновь задачу дискретного программирования в виде
Если об этой задаче ничего неизвестно, то кроме как полного перебора для ее решения применить нельзя. Для ее решения методом ветвей и границ достаточно: 1. Уметь разбивать множество X (переобозначим его через X 0,1)на некоторые подмножества X 1,1,, X 1,2,, X 1,3, .... Каждое из полученных подмножеств, в свою очередь, может быть разбито на подмножества X 2,1, X 2,2, X 2,3, ...,и так далее, вплоть до получения одноэлементных подмножеств. Индексы (i, j) у подмножеств Xi , j означают следующее: i – номер уровня разбиения, j –порядковый номер в уровне. В результате такого разбиения получается дерево подмножеств:
2. На каждом из таких подмножеств Xi , j уметь строить верхние оценки максимального значения функционала, т.е. определять значение xi , j такое, что
Алгоритм метода ветвей и границ. 0 – шаг. Полагаем x' – пустой элемент (в него пока ничего не помещено), Fx' = M = –¥,. В дальнейшем x ' будем называть рекордом, Fx ' – рекордным значением функционала. Строим верхнюю оценку x 0,1 функционала j (x) на подмножестве X 0,1, полагаем V = x 0,1 (V – наименьшая из всех нижних оценок на всех подмножествах). Если в результате этого построения получаем некоторое x Î X 0,1, то x':= x, Fx':= j (x), в противном случае x' и Fx' оставляем без изменения. Если Fx' = V, то x' искомое решение и Fx' – оптимальное значение функционала, в противном случае переходим к следующему шагу. k – ый шаг. Среди всех подмножеств, не подвергнутых разбиению (на дереве разбиения они концевые), ищем подмножество Xr , t , у которого xr , t = V. Разбиваем его на подмножества Xr+ 1, m+ 1, Xr+ 1, m+ 2, Xr+ 1, m+ 3, ..., где m – номер последнего подмножества на (r+ 1)–ом уровне. Для каждого из этих подмножеств строим оценки xr+ 1, m+ 1, xr+ 1, m+ 2, xr+ 1, m+ 3, ..... Обычно эти оценки находятся пересчетом (уточнением) из xr , t . Легко понять, что должно выполняться:
Если в результате этих построений получаем некоторое x Î Xr , t и j (x) >Fx', то x':= x, Fx':= j (x). Отбраковываем все подмножества Xr , t , для которых xr , t £ Fx'. Если в результате оказались отбракованными все подмножества, то x' и Fx' дают искомое решение и алгоритм заканчивает работу. В противном случае полагаем Замечание 1. Нетрудно видеть, что в работе алгоритма участвуют только подмножества, не подвергнутые разбиению (концевые вершины дерева разбиения), которые можно организовывать в виде списка. Если подмножество подвергается разбиению, то оно исключается из списка и заменяется своим разбиением. Замечание 2. Если в исходной задаче функционал минимизируется, то строятся нижние оценки xr , t , т.е. xr , t £max{ j (x) | x Î Xr , t }, и M = +¥.
Алгоритм Ленд–Дойг. Исторически аналог описанного выше алгоритма разработан для задачи целочисленного линейного программирования математиками Ленд и Дойг. Несколько позже эта схема интерпретирована как метод ветвей и границ. В нем для задачи (5.2) множество X 0,1 есть множество всех целочисленных решений задачи. Оценку x 0,1 есть максимум функционала задачи (5.2.) без условий целочисленности. Если при построении x 0,1 получилось нецелочисленное решение, то множество X 0,1 разбивается на два подмножества X 1,1 и X 1,2 следующим образом. Пусть в оптимальном решении задачи (5.2.)
Множество X 1,2есть множество решений системы
Оценки x 1,1, x 1,2 получаются максимизацией функционала задачи (5.2) при ограничениях соответственно (5.6) –(5.9) и (5.10) – (5.12). Заметим, что для построения этих оценок целесообразно к последней симплекс-таблице задачи (5.2) добавлять соответственно ограничения (5.8) и (5.12) и решать задачи двойственным симплекс-методом. Дальнейшие разбиения и построение оценок проводятся аналогично. Рассмотрим следующий пример:
0 – ой шаг. Множество X 0,1состоит из всех целочисленных решений задачи (5.14) – (5.19). Для получения оценки x 0,1 решаем задачу (5.14) – (5.18). После решения этой задачи симплекс-методом последняя симплекс-таблица будет иметь вид:
Оценка x 0,1=7. Решение x 1=4. 44, x 2=2. 56 не является целочисленным. Дерево разбиения примет вид
1–ый шаг. Разбиваем множество X 0,1 на подмножества X 1,1, X 1,2. В качестве переменной, по которой проводим разбиение, берем переменную x 1, которая имеет нецелочисленное значение. Можно взять и переменную x 2. Для подмножества X 1,1 дополнительное ограничение будет иметь вид x 1£4. Добавляем его к последней симплекс-таблице подмножества X 0,1, получим:
Решив эту задачу двойственным симплекс-методом, получим таблицу:
x 1,1=6. 2, x 1=4, x 2=2. 2. Для подмножества X 1,2 дополнительное ограничение будет иметь вид x (1)³5. Добавляем его к последней симплекс-таблице подмножества X 0,1, получим, что задача не имеет решения, т.е. подмножество X 1,2=Æ, x 1,2=¥. Дерево разбиения принимает вид:
На последующих шагах дальнейшему разбиению будет подвергаться подмножество X 1,1,и так далее. Полное дерево разбиения будет иметь вид
На подмножестве X 3,1 получаем целочисленное решение x 1=3, x 2=2 со значением функционала, равным 5, которое принимаем за рекордное. Все подмножества Xr , t , у которых значения xr , t > 5, отбраковываем, тогда x 1=3, x 2=2 становится оптимальным решением. Самостоятельная работа № 11. Решить задачу 4.2 методом Ленд и Дойг, исходные данные по вариантам взять в лабораторной работе №10.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.147.141 (0.007 с.) |

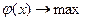 , x Î Х
, x Î Х


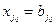 , где
, где  не целое, тогда множество X 1,1 есть множество целочисленных решений системы
не целое, тогда множество X 1,1 есть множество целочисленных решений системы ,
,
 ,
,






