
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Биматричные неантагонистические игры.Содержание книги
Поиск на нашем сайте
Рассмотрим теперь примеры игр [27], в которых, вообще говоря, выигрыш одного игрока во многих случаях не равен проигрышу второго. Игра 1. «Выбор автомобиля». Двое знакомых одновременно выбирают автомобили японских фирм. Первый предпочитает автомобиль марки Хонда, второй — Тойота. Обладание автомобиля любимого типа первый оценивает в а (а > 0) некоторых условных единиц, а второй — в b (b > 0) условных единиц. Полезность автомобиля другого типа для обоих равна нулю. Каждый получает дополнительную выгоду (с > 0), если они выберут одинаковые автомобили, поскольку в таком случае используемое ими запасные части будет совместимым. В этом примере каждый из игроков (мы будем их называть «Игрок 1» и «Игрок 2») имеет две стратегии, которые можно условно назвать «Хонда» и «Тойота». Описанную игру удобно представить в виде таблицы (матрицы) 2´2. В игре имеется четыре исхода: (Хонда, Хонда), (Хонда, Тойота) (Тойота, Хонда) и (Тойота, Тойота). Каждому исходу соответствует своя клетка таблицы; в этой клетке помещаются соответствующие выигрыши участников. Таблица для первого игрока
Таблица для второго игрока
Для анализа игр с двумя игроками целесообразно таблицы объединить. В северо-западном углу выигрыш первого игрока, в юго-восточном – второго.
Левый верхний угол клетки таблицы отведен для первого игрока, нижний правый для второго. Рассмотрим анализ этой игры для случая, когда a =7, b =8, c =3. В этом случае предыдущая таблица будет иметь вид
Выбор первого при условии, что второй игрок принял «Хонда» является «Хонда», при условии, что второй игрок принял «Тойота» так же является «Хонда». Максимальные значения критериев в обоих случаях надчеркнуты. Аналогично для второго игрока, максимальные значения для второго игрока подчеркнуты. В клетке («Хонда»,«Тойота») оказались помеченными оба значения выигрышей, поэтому эта клетка будет состоянием равновесия. В игре, приведенной в следующей таблице нет состояния равновесия, так как в ней нет клетки, в которой одновременно выделены значения обоих критериев.
Игра 2. Пешеход и автомобилист. В игре участвуют пешеход и автомобилист. Каждый из игроков имеет две стратегии: проявлять осторожность (А) и не проявлять осторожности (В). От выбранных стратегий зависит вероятность дорожно–транспортного происшествия (автомобилист собьет пешехода). Если оба ведут себя неосторожно, то вероятность происшествия равна 1/2, если только один ведет себя неосторожно, то вероятность равна 1/10, а если оба осторожны, то вероятность равна 1/100. В случае, если произойдет столкновение, то ущерб пешехода составит 1000 у.е., а ущерб автомобилиста — 200 у.е. Кроме того, осторожное поведение на дороге связано для обоих игроков с издержками в 100 у.е. На примере Игры 2 рассмотрим, каким образом представить в нормальной форме игру, включающую случайность. Для этого нам необходимо задать способ вычисления выигрышей (все остальные элементы нормальной формы здесь уже указаны). Стандартное предположение теории игр состоит в том, что если выигрыш — случайная величина, то игроки предпочитают действия, которые приносят им наибольший ожидаемый выигрыш. Предполагается, что в описании игры случайные выигрыши даны в таком виде, что можно рассчитать их математическое ожидание и использовать в качестве выигрышей в нормальной форме игры. Таким образом, выигрыши выражены в некоторых условных единицах (вовсе не обязательно денежных) и представляют некоторый абстрактный уровень полезности для игрока при данном сочетании стратегий. Пусть оба участника игры проявляют осторожность, то есть реализовался исход (А, А). Если произойдет столкновение, то выигрыш пешехода составит (–1100), а выигрыш водителя — (–300). В противном случае выигрыш пешехода составит (–100), а выигрыш водителя — (–100). Ожидаемые выигрыши равны в этом случае: 1/100* (–1100) + 99/100* (–100) = –110 — для пешехода 1/100* (–200)+99/100*(–100)=–102 — для автомобилиста. Эту информацию вносим в левую верхнюю клетку таблицы.
Из анализа этой игры видно, что состояние равновесия соответствует клетке (A, B), т.е. пешеход должен действовать осторожно, водитель неосторожно. Замечание. В этой игре цифры взяты произвольно, более того не проанализировано взаимодействие «водитель» – «водитель», поэтому водителям вряд ли следует действовать в соответствии с решением в этой игре. Самостоятельная работа № 7. Найти равновесие в играх, где игроки имеют следующие матрицы выигрышей (Номера вариантов записаны в таблице на пересечении строк и столбцов):
А= F=
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.70 (0.005 с.) |

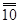
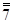
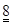
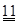
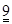
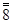
 –102
–102
 ^
^ 
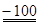
 , B=
, B= 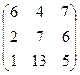 , C=
, C= 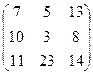 , D=
, D=  , E=
, E= 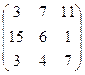 ,
, , G=
, G=  , H=
, H= 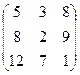 .
.


