

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Принятие решений в условиях неопределенности критерия.
Основная трудность – наличие нескольких критериев, среди которых могут быть неформализованные, по которым следует сравнивать исходы. В этом случае возникает задача принятия решений при так называемом «векторном критерии» [1]-[3].
Случай 1 (построение сверток критериев). Пусть имеется совокупность m критериев:
F 1(x), F 2(x), …, Fm (x), x Î X.
Каждый из этих критериев максимизируемый. Требуется найти решение, которое окажется наилучшим с точки зрения выбираемого критерия. Для принятия решения составляют линейную свертку критериев, получая обобщенный критерий
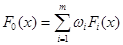 , ,
где wi – вес соответствующего критерия, и решают задачу max F 0(x), x Î X. Одним из примеров в экономике является критерий приведенных затрат, получающийся из противоречивых между собой критериев капитальных и эксплутационных затрат.
Можно привести еще один способ постороения свертки, обычно применяемый при измерении критериев в различных шкалах. Каждый критерий Fi (x), заменяют на 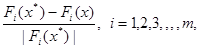 и рассматривают задачу минимизации функционала и рассматривают задачу минимизации функционала
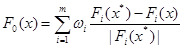 , (1.1) , (1.1)
где 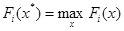 . Эту задачу можно интерпретировать как минимизацию суммы отклонений критериев от их максимальных значений. . Эту задачу можно интерпретировать как минимизацию суммы отклонений критериев от их максимальных значений.
При таком формировании обобщенного критерия может возникнуть несоответствие, связанное с тем, что можно добиться высоких показателей по одним критериям за счет ухудшения показателей по другим критериям. Для ликвидации этих несоответствий вводят дополнительные условия:
F i (x)≥ F i доп (1.2)
и решают задачу (1.1) при этом ограничении.
Случай 2 (перевод критериев в ранг ограничений). Для всех критериев, кроме одного (например первого) задают их наименьшие допустимые значения Fi доп и решают задачу
max F 1(x) (1. 3)
при ограничениях:
Fi (x) ≥ Fi 2 доп., i= 1,2,3,…, m.
Случай 3. (аппроксимационно–комбинаторный подход). Предположим, что для всех критериев j =1,2,3,…, n заданы числа Rj, характеризующие наибольшее допустимое отклонение j –го Fj (x) критерия от его оптимального значения Fj опт, т.е. известно, что решение, подлежащее внедрению должно удовлетворять ограничениям
Fj (x) ≥ Fj опт– Rj, j =1,2,3,…, n
Выбор решения, подлежащего внедрению, осуществляется из получившегося множества W на основе неформальных критериев, которым владеет лицо, принимающее решение. Этот подход предложен В.Р. Хачатуровым [Хачатур] и успешно применялся для дискретных задач.
Случай 4 (оптимизация по Парето). Пусть все критерии F 1(x), F 2(x), …, Fm (x)минимизируемые, т.е. чем меньше их значение, тем предпочтительнее выбор.На множестве всех допустимых решений X, используя формализованные критерии F 1(x), F 2(x), …, Fm (x), x Î X строится порядок. Наибольшие элементы в смысле этого порядка принимаются за оптимальные. Рассмотрим оптимальность по Парето для случая, когда множество X конечное, т.е. X ={ x 1, x 2, x 3,…, xn }.
Будем говорить, что x Î X предпочтительнее y Î X и записывать 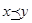 , если для всех i =1,2,3,…, m выполняется Fi (x)£ Fi (y), и существуют i, для которых это неравенство строгое. Таким образом, для любых x, y Î X либо , если для всех i =1,2,3,…, m выполняется Fi (x)£ Fi (y), и существуют i, для которых это неравенство строгое. Таким образом, для любых x, y Î X либо 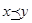 , либо , либо 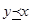 , либо они несравнимы. Наименьший в смысле этого предпочтения элемент является оптимальным по Парето. Напомним, что элемент множества x Î X называется наименьшим в смысле предпочтения , либо они несравнимы. Наименьший в смысле этого предпочтения элемент является оптимальным по Парето. Напомним, что элемент множества x Î X называется наименьшим в смысле предпочтения 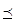 , если не существует x Î X, такого, что , если не существует x Î X, такого, что 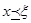 . .
Выбор решения, подлежащего внедрению, осуществляется из множества Парето P на основе неформальных критериев, которым владеет лицо, принимающее решение.
Примеры.
Построение линейной свертки. Для демонстрации построения линейной свертки рассмотрим пример, приведенный в следующей таблице:
|
| Элементы множества X
| Максимальный элемент по критерию
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
|
|
|
|
|
|
|
|
|
|
| x 4, x 10
| |
|
|
|
|
|
|
|
|
|
|
| x 2
| |
|
|
|
|
|
|
|
|
|
|
| x 7
| |
|
|
|
|
|
|
|
|
|
|
| x 5
| |
|
|
|
|
|
|
|
|
|
|
| x 3
|
В ней X ={ x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9, x 10}, критерии F 1(x), F 2(x), …, F 5(x). В каждой строке таблицы указаны значения соответствующего критерия. Все критерии максимизируемые.
Максимальные элементы по каждому критерию приведены в крайнем правом столбце.
Зададим коэффициенты свертки, в следующей таблице они справа.
|
| Элементы множества X
| Коэфф. свертки
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
|
|
|
|
|
|
|
|
|
|
| 0,1
| |
|
|
|
|
|
|
|
|
|
|
| 0,3
| |
|
|
|
|
|
|
|
|
|
|
| 0,1
| |
|
|
|
|
|
|
|
|
|
|
| 0,4
| |
|
|
|
|
|
|
|
|
|
|
| 0,1
|
Таблица для свертки критериев имеет вид:
|
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Линейная свертка (F 0(x))
| 4,7
|
| 3,4
| 3,6
| 5,3
| 3,2
| 5,3
| 2,4
| 4,7
| 3,3
| Ясно, что F 0(x 5)= F 0(x 7)=  =5,3, т.е. оптимальными являются элементы x 5, x 7. =5,3, т.е. оптимальными являются элементы x 5, x 7.
Аппроксимационно–комбинаторный подход.
|
| Элементы множества X
| Допустимое отклонение от оптимума
| Допустимые решения по критерию
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
|
|
|
|
|
|
|
|
|
|
|
| x 4, x 10, x 5, x 7, x 9
| |
|
|
|
|
|
|
|
|
|
|
|
| x 7, x 2, x 7, x 9
| |
|
|
|
|
|
|
|
|
|
|
|
| x 5, x 7, x 9
| |
|
|
|
|
|
|
|
|
|
|
|
| x 5, x 9, x 7
| |
|
|
|
|
|
|
|
|
|
|
|
| x 3, x 7, x 9
|
Множество допустимых решений одновременно по всем критериям { x 7, x 9}. Среди эти решений ЛПР произведет окончательный выбор.
Оптимизация по Парето
Рассмотрим пример, приведенный в следующей таблице:
|
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
В ней X ={ x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9, x 10}, критерии F 1(x), F 2(x), …, F 5(x). В каждой строке таблицы указаны значения соответствующей функции. В ней 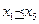 , x 8 и x 10 несравнимы между собой, они также являются оптимальными по Парето, так как не существует элементов, предпочтительнее, чем они. , x 8 и x 10 несравнимы между собой, они также являются оптимальными по Парето, так как не существует элементов, предпочтительнее, чем они.
Самостоятельная работа №1.
Для данных, приведенных далее в таблицах выполнить:
1) Найти максимальные решения по каждому критерию.
2) Построить линейную свертку критериев и найти оптимальное решение, коэффициенты свертки взять из рассмотренного выше примера.
3) Найти множество решений в задаче согласно аппроксимационно–комбинаторного подхода, значения допустимых отклонений от оптимума взять из ранее решенного примера.
4) Считая все критерии, приведенные в таблице, минимизируемые, привести решения
а) x и у, для которых 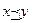
б) x и у, которые несравнимые по предпочтению 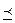 , ,
в) оптимальные по Парето.
Таблицы вариантов заданий:
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,1
| 1,3
| 1,3
| 1,5
| 0,3
| 2,0
| 0,0
| 1,4
| 0,3
| 0,0
| |
| 0,8
| 2,0
| 2,0
| 0,6
| 1,3
| 1,8
| 0,3
| 2,0
| 1,3
| 0,7
| |
| 1,7
| 1,8
| 1,8
| 0,0
| 2,0
| 0,9
| 1,3
| 1,7
| 2,0
| 1,6
| |
| 2,0
| 0,9
| 0,9
| 0,3
| 1,8
| 0,1
| 2,0
| 0,8
| 1,8
| 2,0
| |
| 1,3
| 0,1
| 0,1
| 1,3
| 0,9
| 0,2
| 1,8
| 0,1
| 0,9
| 1,4
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,8
| 2,0
| 2,0
| 0,6
| 1,3
| 1,8
| 0,3
| 2,0
| 1,3
| 0,7
| |
| 1,7
| 1,8
| 1,8
| 0,0
| 2,0
| 0,9
| 1,3
| 1,7
| 2,0
| 1,6
| |
| 2,0
| 0,9
| 0,9
| 0,3
| 1,8
| 0,1
| 2,0
| 0,8
| 1,8
| 2,0
| |
| 1,3
| 0,1
| 0,1
| 1,3
| 0,9
| 0,2
| 1,8
| 0,1
| 0,9
| 1,4
| |
| 0,4
| 0,2
| 0,2
| 2,0
| 0,1
| 1,0
| 0,9
| 0,2
| 0,1
| 0,5
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,7
| 1,8
| 1,8
| 0,0
| 2,0
| 0,9
| 1,3
| 1,7
| 2,0
| 1,6
| |
| 2,0
| 0,9
| 0,9
| 0,3
| 1,8
| 0,1
| 2,0
| 0,8
| 1,8
| 2,0
| |
| 1,3
| 0,1
| 0,1
| 1,3
| 0,9
| 0,2
| 1,8
| 0,1
| 0,9
| 1,4
| |
| 0,4
| 0,2
| 0,2
| 2,0
| 0,1
| 1,0
| 0,9
| 0,2
| 0,1
| 0,5
| |
| 0,0
| 1,0
| 1,0
| 1,8
| 0,2
| 1,8
| 0,1
| 1,1
| 0,2
| 0,0
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 2,0
| 0,9
| 0,9
| 0,3
| 1,8
| 0,1
| 2,0
| 0,8
| 1,8
| 2,0
| |
| 1,3
| 0,1
| 0,1
| 1,3
| 0,9
| 0,2
| 1,8
| 0,1
| 0,9
| 1,4
| |
| 0,4
| 0,2
| 0,2
| 2,0
| 0,1
| 1,0
| 0,9
| 0,2
| 0,1
| 0,5
| |
| 0,0
| 1,0
| 1,0
| 1,8
| 0,2
| 1,8
| 0,1
| 1,1
| 0,2
| 0,0
| |
| 0,5
| 1,8
| 1,8
| 0,9
| 1,0
| 1,9
| 0,2
| 1,9
| 1,0
| 0,4
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,3
| 0,1
| 0,1
| 1,3
| 0,9
| 0,2
| 1,8
| 0,1
| 0,9
| 1,4
| |
| 0,4
| 0,2
| 0,2
| 2,0
| 0,1
| 1,0
| 0,9
| 0,2
| 0,1
| 0,5
| |
| 0,0
| 1,0
| 1,0
| 1,8
| 0,2
| 1,8
| 0,1
| 1,1
| 0,2
| 0,0
| |
| 0,5
| 1,8
| 1,8
| 0,9
| 1,0
| 1,9
| 0,2
| 1,9
| 1,0
| 0,4
| |
| 1,5
| 1,9
| 1,9
| 0,1
| 1,8
| 1,1
| 1,0
| 1,9
| 1,8
| 1,4
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,4
| 0,2
| 0,2
| 2,0
| 0,1
| 1,0
| 0,9
| 0,2
| 0,1
| 0,5
| |
| 0,0
| 1,0
| 1,0
| 1,8
| 0,2
| 1,8
| 0,1
| 1,1
| 0,2
| 0,0
| |
| 0,5
| 1,8
| 1,8
| 0,9
| 1,0
| 1,9
| 0,2
| 1,9
| 1,0
| 0,4
| |
| 1,5
| 1,9
| 1,9
| 0,1
| 1,8
| 1,1
| 1,0
| 1,9
| 1,8
| 1,4
| |
| 2,0
| 1,1
| 1,1
| 0,2
| 1,9
| 0,2
| 1,8
| 1,0
| 1,9
| 2,0
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,0
| 1,0
| 1,0
| 1,8
| 0,2
| 1,8
| 0,1
| 1,1
| 0,2
| 0,0
| |
| 0,5
| 1,8
| 1,8
| 0,9
| 1,0
| 1,9
| 0,2
| 1,9
| 1,0
| 0,4
| |
| 1,5
| 1,9
| 1,9
| 0,1
| 1,8
| 1,1
| 1,0
| 1,9
| 1,8
| 1,4
| |
| 2,0
| 1,1
| 1,1
| 0,2
| 1,9
| 0,2
| 1,8
| 1,0
| 1,9
| 2,0
| |
| 1,6
| 0,2
| 0,2
| 1,0
| 1,1
| 0,0
| 1,9
| 0,2
| 1,1
| 1,7
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,5
| 1,8
| 1,8
| 0,9
| 1,0
| 1,9
| 0,2
| 1,9
| 1,0
| 0,4
| |
| 1,5
| 1,9
| 1,9
| 0,1
| 1,8
| 1,1
| 1,0
| 1,9
| 1,8
| 1,4
| |
| 2,0
| 1,1
| 1,1
| 0,2
| 1,9
| 0,2
| 1,8
| 1,0
| 1,9
| 2,0
| |
| 1,6
| 0,2
| 0,2
| 1,0
| 1,1
| 0,0
| 1,9
| 0,2
| 1,1
| 1,7
| |
| 0,6
| 0,0
| 0,0
| 1,8
| 0,2
| 0,7
| 1,1
| 0,1
| 0,2
| 0,7
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,5
| 1,9
| 1,9
| 0,1
| 1,8
| 1,1
| 1,0
| 1,9
| 1,8
| 1,4
| |
| 2,0
| 1,1
| 1,1
| 0,2
| 1,9
| 0,2
| 1,8
| 1,0
| 1,9
| 2,0
| |
| 1,6
| 0,2
| 0,2
| 1,0
| 1,1
| 0,0
| 1,9
| 0,2
| 1,1
| 1,7
| |
| 0,6
| 0,0
| 0,0
| 1,8
| 0,2
| 0,7
| 1,1
| 0,1
| 0,2
| 0,7
| |
| 0,0
| 0,7
| 0,7
| 1,9
| 0,0
| 1,7
| 0,2
| 0,8
| 0,0
| 0,0
|
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 2,0
| 1,1
| 1,1
| 0,2
| 1,9
| 0,2
| 1,8
| 1,0
| 1,9
| 2,0
| |
| 1,6
| 0,2
| 0,2
| 1,0
| 1,1
| 0,0
| 1,9
| 0,2
| 1,1
| 1,7
| |
| 0,6
| 0,0
| 0,0
| 1,8
| 0,2
| 0,7
| 1,1
| 0,1
| 0,2
| 0,7
| |
| 0,0
| 0,7
| 0,7
| 1,9
| 0,0
| 1,7
| 0,2
| 0,8
| 0,0
| 0,0
| |
| 0,3
| 1,7
| 1,7
| 1,1
| 0,7
| 2,0
| 0,0
| 1,7
| 0,7
| 0,2
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,6
| 0,2
| 0,2
| 1,0
| 1,1
| 0,0
| 1,9
| 0,2
| 1,1
| 1,7
| |
| 0,6
| 0,0
| 0,0
| 1,8
| 0,2
| 0,7
| 1,1
| 0,1
| 0,2
| 0,7
| |
| 0,0
| 0,7
| 0,7
| 1,9
| 0,0
| 1,7
| 0,2
| 0,8
| 0,0
| 0,0
| |
| 0,3
| 1,7
| 1,7
| 1,1
| 0,7
| 2,0
| 0,0
| 1,7
| 0,7
| 0,2
| |
| 1,2
| 2,0
| 2,0
| 0,2
| 1,7
| 1,4
| 0,7
| 2,0
| 1,7
| 1,1
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,6
| 0,0
| 0,0
| 1,8
| 0,2
| 0,7
| 1,1
| 0,1
| 0,2
| 0,7
| |
| 0,0
| 0,7
| 0,7
| 1,9
| 0,0
| 1,7
| 0,2
| 0,8
| 0,0
| 0,0
| |
| 0,3
| 1,7
| 1,7
| 1,1
| 0,7
| 2,0
| 0,0
| 1,7
| 0,7
| 0,2
| |
| 1,2
| 2,0
| 2,0
| 0,2
| 1,7
| 1,4
| 0,7
| 2,0
| 1,7
| 1,1
| |
| 1,9
| 1,4
| 1,4
| 0,0
| 2,0
| 0,5
| 1,7
| 1,3
| 2,0
| 1,9
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,0
| 0,7
| 0,7
| 1,9
| 0,0
| 1,7
| 0,2
| 0,8
| 0,0
| 0,0
| |
| 0,3
| 1,7
| 1,7
| 1,1
| 0,7
| 2,0
| 0,0
| 1,7
| 0,7
| 0,2
| |
| 1,2
| 2,0
| 2,0
| 0,2
| 1,7
| 1,4
| 0,7
| 2,0
| 1,7
| 1,1
| |
| 1,9
| 1,4
| 1,4
| 0,0
| 2,0
| 0,5
| 1,7
| 1,3
| 2,0
| 1,9
| |
| 1,8
| 0,5
| 0,5
| 0,7
| 1,4
| 0,0
| 2,0
| 0,4
| 1,4
| 1,9
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,3
| 1,7
| 1,7
| 1,1
| 0,7
| 2,0
| 0,0
| 1,7
| 0,7
| 0,2
| |
| 1,2
| 2,0
| 2,0
| 0,2
| 1,7
| 1,4
| 0,7
| 2,0
| 1,7
| 1,1
| |
| 1,9
| 1,4
| 1,4
| 0,0
| 2,0
| 0,5
| 1,7
| 1,3
| 2,0
| 1,9
| |
| 1,8
| 0,5
| 0,5
| 0,7
| 1,4
| 0,0
| 2,0
| 0,4
| 1,4
| 1,9
| |
| 0,9
| 0,0
| 0,0
| 1,7
| 0,5
| 0,5
| 1,4
| 0,0
| 0,5
| 1,0
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,2
| 2,0
| 2,0
| 0,2
| 1,7
| 1,4
| 0,7
| 2,0
| 1,7
| 1,1
| |
| 1,9
| 1,4
| 1,4
| 0,0
| 2,0
| 0,5
| 1,7
| 1,3
| 2,0
| 1,9
| |
| 1,8
| 0,5
| 0,5
| 0,7
| 1,4
| 0,0
| 2,0
| 0,4
| 1,4
| 1,9
| |
| 0,9
| 0,0
| 0,0
| 1,7
| 0,5
| 0,5
| 1,4
| 0,0
| 0,5
| 1,0
| |
| 0,1
| 0,5
| 0,5
| 2,0
| 0,0
| 1,4
| 0,5
| 0,6
| 0,0
| 0,2
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,9
| 1,4
| 1,4
| 0,0
| 2,0
| 0,5
| 1,7
| 1,3
| 2,0
| 1,9
| |
| 1,8
| 0,5
| 0,5
| 0,7
| 1,4
| 0,0
| 2,0
| 0,4
| 1,4
| 1,9
| |
| 0,9
| 0,0
| 0,0
| 1,7
| 0,5
| 0,5
| 1,4
| 0,0
| 0,5
| 1,0
| |
| 0,1
| 0,5
| 0,5
| 2,0
| 0,0
| 1,4
| 0,5
| 0,6
| 0,0
| 0,2
| |
| 0,1
| 1,4
| 1,4
| 1,4
| 0,5
| 2,0
| 0,0
| 1,5
| 0,5
| 0,1
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,8
| 0,5
| 0,5
| 0,7
| 1,4
| 0,0
| 2,0
| 0,4
| 1,4
| 1,9
| |
| 0,9
| 0,0
| 0,0
| 1,7
| 0,5
| 0,5
| 1,4
| 0,0
| 0,5
| 1,0
| |
| 0,1
| 0,5
| 0,5
| 2,0
| 0,0
| 1,4
| 0,5
| 0,6
| 0,0
| 0,2
| |
| 0,1
| 1,4
| 1,4
| 1,4
| 0,5
| 2,0
| 0,0
| 1,5
| 0,5
| 0,1
| |
| 0,9
| 2,0
| 2,0
| 0,5
| 1,4
| 1,6
| 0,5
| 2,0
| 1,4
| 0,8
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,9
| 0,0
| 0,0
| 1,7
| 0,5
| 0,5
| 1,4
| 0,0
| 0,5
| 1,0
| |
| 0,1
| 0,5
| 0,5
| 2,0
| 0,0
| 1,4
| 0,5
| 0,6
| 0,0
| 0,2
| |
| 0,1
| 1,4
| 1,4
| 1,4
| 0,5
| 2,0
| 0,0
| 1,5
| 0,5
| 0,1
| |
| 0,9
| 2,0
| 2,0
| 0,5
| 1,4
| 1,6
| 0,5
| 2,0
| 1,4
| 0,8
| |
| 1,8
| 1,6
| 1,6
| 0,0
| 2,0
| 0,7
| 1,4
| 1,6
| 2,0
| 1,7
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,1
| 0,5
| 0,5
| 2,0
| 0,0
| 1,4
| 0,5
| 0,6
| 0,0
| 0,2
| |
| 0,1
| 1,4
| 1,4
| 1,4
| 0,5
| 2,0
| 0,0
| 1,5
| 0,5
| 0,1
| |
| 0,9
| 2,0
| 2,0
| 0,5
| 1,4
| 1,6
| 0,5
| 2,0
| 1,4
| 0,8
| |
| 1,8
| 1,6
| 1,6
| 0,0
| 2,0
| 0,7
| 1,4
| 1,6
| 2,0
| 1,7
| |
| 1,9
| 0,7
| 0,7
| 0,5
| 1,6
| 0,0
| 2,0
| 0,6
| 1,6
| 2,0
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,1
| 1,4
| 1,4
| 1,4
| 0,5
| 2,0
| 0,0
| 1,5
| 0,5
| 0,1
| |
| 0,9
| 2,0
| 2,0
| 0,5
| 1,4
| 1,6
| 0,5
| 2,0
| 1,4
| 0,8
| |
| 1,8
| 1,6
| 1,6
| 0,0
| 2,0
| 0,7
| 1,4
| 1,6
| 2,0
| 1,7
| |
| 1,9
| 0,7
| 0,7
| 0,5
| 1,6
| 0,0
| 2,0
| 0,6
| 1,6
| 2,0
| |
| 1,2
| 0,0
| 0,0
| 1,4
| 0,7
| 0,3
| 1,6
| 0,0
| 0,7
| 1,3
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,9
| 2,0
| 2,0
| 0,5
| 1,4
| 1,6
| 0,5
| 2,0
| 1,4
| 0,8
| |
| 1,8
| 1,6
| 1,6
| 0,0
| 2,0
| 0,7
| 1,4
| 1,6
| 2,0
| 1,7
| |
| 1,9
| 0,7
| 0,7
| 0,5
| 1,6
| 0,0
| 2,0
| 0,6
| 1,6
| 2,0
| |
| 1,2
| 0,0
| 0,0
| 1,4
| 0,7
| 0,3
| 1,6
| 0,0
| 0,7
| 1,3
| |
| 0,3
| 0,3
| 0,3
| 2,0
| 0,0
| 1,2
| 0,7
| 0,3
| 0,0
| 0,4
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,8
| 1,6
| 1,6
| 0,0
| 2,0
| 0,7
| 1,4
| 1,6
| 2,0
| 1,7
| |
| 1,9
| 0,7
| 0,7
| 0,5
| 1,6
| 0,0
| 2,0
| 0,6
| 1,6
| 2,0
| |
| 1,2
| 0,0
| 0,0
| 1,4
| 0,7
| 0,3
| 1,6
| 0,0
| 0,7
| 1,3
| |
| 0,3
| 0,3
| 0,3
| 2,0
| 0,0
| 1,2
| 0,7
| 0,3
| 0,0
| 0,4
| |
| 0,0
| 1,2
| 1,2
| 1,6
| 0,3
| 1,9
| 0,0
| 1,3
| 0,3
| 0,0
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,9
| 0,7
| 0,7
| 0,5
| 1,6
| 0,0
| 2,0
| 0,6
| 1,6
| 2,0
| |
| 1,2
| 0,0
| 0,0
| 1,4
| 0,7
| 0,3
| 1,6
| 0,0
| 0,7
| 1,3
| |
| 0,3
| 0,3
| 0,3
| 2,0
| 0,0
| 1,2
| 0,7
| 0,3
| 0,0
| 0,4
| |
| 0,0
| 1,2
| 1,2
| 1,6
| 0,3
| 1,9
| 0,0
| 1,3
| 0,3
| 0,0
| |
| 0,7
| 1,9
| 1,9
| 0,7
| 1,2
| 1,8
| 0,3
| 2,0
| 1,2
| 0,6
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,2
| 0,0
| 0,0
| 1,4
| 0,7
| 0,3
| 1,6
| 0,0
| 0,7
| 1,3
| |
| 0,3
| 0,3
| 0,3
| 2,0
| 0,0
| 1,2
| 0,7
| 0,3
| 0,0
| 0,4
| |
| 0,0
| 1,2
| 1,2
| 1,6
| 0,3
| 1,9
| 0,0
| 1,3
| 0,3
| 0,0
| |
| 0,7
| 1,9
| 1,9
| 0,7
| 1,2
| 1,8
| 0,3
| 2,0
| 1,2
| 0,6
| |
| 1,6
| 1,8
| 1,8
| 0,0
| 1,9
| 1,0
| 1,2
| 1,8
| 1,9
| 1,5
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,3
| 0,3
| 0,3
| 2,0
| 0,0
| 1,2
| 0,7
| 0,3
| 0,0
| 0,4
| |
| 0,0
| 1,2
| 1,2
| 1,6
| 0,3
| 1,9
| 0,0
| 1,3
| 0,3
| 0,0
| |
| 0,7
| 1,9
| 1,9
| 0,7
| 1,2
| 1,8
| 0,3
| 2,0
| 1,2
| 0,6
| |
| 1,6
| 1,8
| 1,8
| 0,0
| 1,9
| 1,0
| 1,2
| 1,8
| 1,9
| 1,5
| |
| 2,0
| 1,0
| 1,0
| 0,3
| 1,8
| 0,2
| 1,9
| 0,9
| 1,8
| 2,0
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 0,7
| 1,9
| 1,9
| 0,7
| 1,2
| 1,8
| 0,3
| 2,0
| 1,2
| 0,6
| |
| 1,6
| 1,8
| 1,8
| 0,0
| 1,9
| 1,0
| 1,2
| 1,8
| 1,9
| 1,5
| |
| 2,0
| 1,0
| 1,0
| 0,3
| 1,8
| 0,2
| 1,9
| 0,9
| 1,8
| 2,0
| |
| 1,5
| 0,2
| 0,2
| 1,2
| 1,0
| 0,1
| 1,8
| 0,1
| 1,0
| 1,6
| |
| 0,5
| 0,1
| 0,1
| 1,9
| 0,2
| 0,9
| 1,0
| 0,1
| 0,2
| 0,6
| | Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| x 7
| x 8
| x 9
| x 10
| | Критерии
|
| 1,6
| 1,8
| 1,8
| 0,0
| 1,9
| 1,0
| 1,2
| 1,8
| 1,9
| 1,5
| |
| 2,0
| 1,0
| 1,0
| 0,3
| 1,8
| 0,2
| 1,9
| 0,9
| 1,8
| 2,0
| |
| 1,5
| 0,2
| 0,2
| 1,2
| 1,0
| 0,1
| 1,8
| 0,1
| 1,0
| 1,6
| |
| 0,5
| 0,1
| 0,1
| 1,9
| 0,2
| 0,9
| 1,0
| 0,1
| 0,2
| 0,6
| |
| 0,0
| 0,9
| 0,9
| 1,8
| 0,1
| 1,8
| 0,2
| 1,0
| 0,1
| 0,0
|
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| Элементы множества X
| | x 1
| x 2
| x 3
| x
| Поделиться:
| |
|



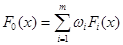 ,
,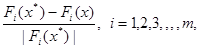 и рассматривают задачу минимизации функционала
и рассматривают задачу минимизации функционала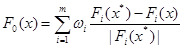 , (1.1)
, (1.1)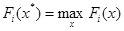 . Эту задачу можно интерпретировать как минимизацию суммы отклонений критериев от их максимальных значений.
. Эту задачу можно интерпретировать как минимизацию суммы отклонений критериев от их максимальных значений.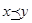 , если для всех i =1,2,3,…, m выполняется Fi (x)£ Fi (y), и существуют i, для которых это неравенство строгое. Таким образом, для любых x, y Î X либо
, если для всех i =1,2,3,…, m выполняется Fi (x)£ Fi (y), и существуют i, для которых это неравенство строгое. Таким образом, для любых x, y Î X либо 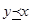 , либо они несравнимы. Наименьший в смысле этого предпочтения элемент является оптимальным по Парето. Напомним, что элемент множества x Î X называется наименьшим в смысле предпочтения
, либо они несравнимы. Наименьший в смысле этого предпочтения элемент является оптимальным по Парето. Напомним, что элемент множества x Î X называется наименьшим в смысле предпочтения 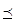 , если не существует x Î X, такого, что
, если не существует x Î X, такого, что 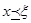 .
. =5,3, т.е. оптимальными являются элементы x 5, x 7.
=5,3, т.е. оптимальными являются элементы x 5, x 7.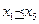 , x 8 и x 10 несравнимы между собой, они также являются оптимальными по Парето, так как не существует элементов, предпочтительнее, чем они.
, x 8 и x 10 несравнимы между собой, они также являются оптимальными по Парето, так как не существует элементов, предпочтительнее, чем они.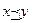
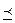 ,
,


