Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм поиска исходного базисного дерева.Содержание книги
Поиск на нашем сайте При поиске исходного базисного дерева применяют описанный выше метод для следующей «искусственной» задачи. Строим граф G =á E, V, H ñ, в котором E = E È{ i 0}, где i 0 – дополнительная вершина, V = V È V 1È V 2, где V 1 – множество дополнительных дуг, направленных от вершин – пунктов производства к дополнительной вершине i 0, V 2 – множество дополнительных дуг, направляемых от i 0 к промежуточным вершинам и вершинам–пунктам потребления. Для v Î V полагаем cv =0; для v Î V 1полагаем cv =1; для v Î V 2 полагаем cv =1. Полагаем В качестве исходного базисного дерева берется подграф G =á E, V 1 È V 2, H ñ. Если в результате решения этой задачи оказалось, что оптимальное значение функционала строго больше нуля, то исходная задача(6.1) –(6.3) решения не имеет, в противном случае будет получено базисное дерево исходной задачи. Пример. Решим задачу, представленную графом, изображенным на рис. 6. 1
Рис. 6.1. Вершины графа обозначены цифрами от 1 до 9, обведенными кругом. Около дуг написаны их имена. Рядом с каждой вершиной проставлены мощности вершин: b 1= – 3; b 2= – 1; b 3= – 7; b 4=0; b 5=0; b 6=5; b 7=2; b 8=4; b 9=0. Стоимость перевозок по дугам задана следующей таблицей (каждая дуга задана парой инцидентных вершин).
Примем за исходный базис дерево, дуги которого выделены жирной линией (см. Рис. 6.1). Шаг 1. Определим объем перевозок для исходного базисного дерева.
Общая стоимость перевозок составит
Определим потенциалы вершин: u 9:= 0; u 7= u 9 – u 8= u 7 + u 4= u 7 – u 5= u 4 + u 6= u 5 + u 3= u 4 – u 1= u 4 – u 2= u 4 – Проверим полученное решение на оптимальность: На дуге v 10 u 7 > u 2 +
Рис. 6.2
q =min(1,6)=1;
Шаг 2. Пересчитаем объем перевозок для нового базиса:
Определим потенциалы вершин. u 1= – 9; u 2= – 8; u 3= – 8; u 4= – 7; u 5= – 6; u 6= – 5; u 7= – 3; u 8= – 2; u 9:=0; Проверим полученное решение на оптимальность. На дуге v 6 u 6 >u 3 +
q =min(7,5,5)=5. Шаг 3. Пересчитаем объемы перевозок для нового базиса:
Определим потенциалы вершин u 1= – 9; u 2= – 8; u 3= – 8; u 4= – 7; u 5= – 6; u 6= – 6; u 7= – 3; u 8= – 2; u 9:=0. Полученное решение оптимально. Дерево перевозок изображено на рис. 6.3. Стоимость перевозок составит:
Рис. 6.3
Самостоятельная работа 13. Задание. Определить объемы перевозок минимальной стоимости для графа, изображенного на рисунке примера, стоимости перевозок по вариантам приведены в таблице:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 .
.
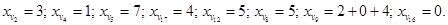

 = – 3;
= – 3; = – 2;
= – 2; = – 7;
= – 7; = – 6;
= – 6; = – 5;
= – 5; = – 8;
= – 8; = – 9;
= – 9;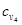 = – 8;
= – 8; , следовательно, дугу v 10 вводим в базис. Возникший цикл (см. Рис. 6.2) обходим в направлении дуги v 10.
, следовательно, дугу v 10 вводим в базис. Возникший цикл (см. Рис. 6.2) обходим в направлении дуги v 10.
 q;
q;  1 – q;
1 – q;  6 – q;
6 – q; =0, дугу v 4 выводим из базиса.
=0, дугу v 4 выводим из базиса.
 3;
3;  7;
7;  4;
4;  5;
5;  5;
5;  0; f =48.
0; f =48. , следовательно, решение не оптимально и дугу v 6 вводим в базис. Возникший цикл обходим в направлении дуги v 6,
, следовательно, решение не оптимально и дугу v 6 вводим в базис. Возникший цикл обходим в направлении дуги v 6, = q;
= q;  =7 – q;
=7 – q;  =5 – q;
=5 – q;  =5 – q;
=5 – q;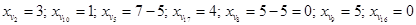 .
.