
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм безусловной векторной оптимизаци.Содержание книги
Поиск на нашем сайте
Предлагаемый ниже алгоритм является развитием градиентных методов и метода возможных направлений Зойтендейка. Так задача ZS (y)для однокритериальной задачи безусловной оптимизации в качестве направления s вырабатывает Алгоритм. 0 –ой шаг. В качестве х 0задаем произвольную точку из Rn. k – ый шаг (k = 0, 1, 2, …). Полагаем
где значения sk , sk получены из решения задачи ZS (xk). lk выбирается следующим образом: 1. Выбираем некоторое l (одно на всех итерациях) и полагаем lk = l. 2. Вычисляем j i (x)= j i (xk + l sk sk), iÎ M. 3. Если для всех
то lk является искомым, в противном случае полагаем lk = a lk , где a Î (0,1)и переходим к шагу 2. Последовательности { xk },{ sk },{ sk }обрываем, если для некоторого k в точке xk оказалось sk =0,в этом случае при выполнении достаточных условий точка xk являются оптимумом по Слейтеру. Пример. Для задачи j 1(x)= x 12 + x 22 ® min, j 2(x)= x 12 + (x 2 – 4)2 ® min, j 3(x)=(x 1 – 4)2 + x 22 ® min, j 4(x)=(x 1 – 4)2 + (x 2 – 4)2 ® min. проверить на оптимальность точку y =(2,2) T. Решение. В этой задаче множество I = Æ, поэтому задача ZS (y)примет вид: Задача ZS (y).
Подставляя в (2.9) значения градиентов j i' (y)в точке у = (2, 2),получим max s, 4 s 1 + 4 s 2 + s £0, 4 s 1 – 4 s 2 + s £0, – 4 s 1 + 4 s 2 + s £0, – 4 s 1 – 4 s 2 + s £0, – 1£ s 1£1, – 1£ s 2£1. Проведя замену переменных sj = s'j – 1, j= 1,2, получим max s, 4 s' 1 + 4 s' 2 + s £8, 4 s' 1 – 4 s' 2 + s £0, – 4 s' 1 + 4 s' 2 + s £0, – 4 s' 1 – 4 s' 2 + s £ – 8, s' 1 £ 2, s' (2) £ 2, s' 1³0, s' 2³0, s ³0. Решая эту задачу симплекс – методом, получаем, что максимальное значение s =0. Это означает, что точка y =(2,2) оптимальна по Слейтеру Самостоятельная работа №3. Для задачи j 1(x)=(x 1 – a 1)2 + (x 2 – b 1)2 ® min, j 2(x)=(x 1 – a 2)2 + (x 2 – b 2)2 ® min, j 3(x)=(x 1 – a 3)2 + (x 2 – b 3)2 ® min, j 4(x)=(x 1 – a 4)2 + (x 2 – b 4)2 ® min. проверить на оптимальность точки: y =(y 1, y 2) T, z =(z 1, z 2) T. Если точка не является оптимальной, то для нее указать подходящее направление. Варианты заданий взять в следующей таблице:
Теорема Куна–Таккера для задачи выпуклого векторного программирования
Рассмотрим анализ задачи выпуклого векторного программирования на необходимые и достаточные условия существования оптимальной точки по Слейтеру. Для этого приведем аналог известной теоремы Куна – Таккера. Теорема Куна–Таккера 2. 17. Пусть множество X удовлетворяет условию регулярности R 2. Для того, чтобы точка y Î X была точкой оптимума по Слейтеру, необходимо и достаточно существование таких ui, i Î(M È I (y)), для которых справедлива система
Приведем пример, иллюстрирующий применение теоремы Куна – Таккера к анализу задачи (2.1), (2.2). Пример. Для задачи j 1(x)= x 12 + x 22 ® min, j 2(x)= x 12 + (x 2 – 4)2 ® min, j 3(x)=(x 1 – 4)2 + x 22 ® min, j 4(x)=(x 1 – 4)2 + (x 2 – 4)2 ® min.
проверить на оптимальность по Слейтеру точку y =(2,2) T. Решение. Составим для этой задачи систему вида (2.15). Для этого, подставив в нее значения градиентов j' i (y), получим
Нетрудно видеть, что составленнаясистема разрешима и имеет следующие решения:(0. 50,0. 00,0. 00,0. 50) T, (0. 00,0. 50,0. 50,0. 00) T, (0. 25,0. 25,0. 25,0. 25) T. В общем случае проверить разрешимость подобных задач можно симплекс-методом. Продемонстрируем это. Введем в систему (2.15) искусственные переменные zj, j =1,2,3и построим задачу:
Если в этой задаче F =0,т.е. z 1=0, z 2=0, z 3=0, то система (2.15) разрешима, если F >0, то система (2.15) не имеет решения. Самостоятельная работа № 4. Для задачи j 1(x)=(x 1 – a 1)2 + (x 2 – b 1)2 ® min, j 2(x)=(x 1 – a 2)2 + (x 2 – b 2)2 ® min, j 3(x)=(x 1 – a 3)2 + (x 2 – b 3)2 ® min, j 4(x)=(x 1 – a 4)2 + (x 2 – b 4)2 ® min.
проверить на оптимальность точки: y =(y 1, y 2) T, z =(z 1, z 2) T. Варианты заданий взять из лабораторной работы 3.
Некоторые задачи теория игр Теория игр – это раздел математики, в котором исследуются математические модели принятия решений в условиях конфликта, т. е. в условиях, когда каждая из оперирующих сторон стремится оптимизировать свой критерий эффективности, оказывая при этом влияние на критерии эффективности других оперирующих сторон. Теорию игр можно рассматривать как составную часть исследования операций. Формально игру можно определить в следующем виде: Нормальная форма игры: G =á I; Xi, i Î I; ji (x), где I – множество игроков, I ={1,2,3,…, N }, для i –го игрока Xi, – множество стратегий i –го игрока, он осуществляет выбор xi Î Xi, ji (x) – критерий (выигрыш), по которому i –ый игрок оценивает свое состояние в игре. В силу того, что Равновесие по Нешу в игре. Точку x* =(x* 1, x* 2, x* 3,…, x*i, …, x*N)Î X будем называть состоянием равновесия по Нешу, если для каждого игрока i Î I выполняется соотношение
т.е. получаем, что из состояний равновесия не выгодно выходить ни одному (только одному) игроку, так как в этом случае он уменьшает свой выигрыш. Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д. В зависимости от количества игроков N различают игры двух и более чем двух игроков. Первые из них наиболее изучены. Игры трёх и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения. Чем больше игроков, тем больше проблем. По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если при этом N =2, то биматричной, так как в этом случае функции выигрыша ji (x)= ji (x 1, x 2) можно представить матрицами. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий игра называется бесконечной. По характеру взаимодействия субъектов игры делятся на: 1) бескоалиционные игры – в них игроки не имеют права вступать какие-либо объединения для выбора согласованных стратегий, т.е. не имеют права образовывать коалиции; 2) коалиционные (кооперативные) игры – в них игроки могут вступать в коалиции, состав которых заранее определен. Члены одной коалиции могут обмениваться информацией и принимать полностью согласованные решения. По характеру выигрышей игры делятся н а: антагонистические или игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой. По виду функций выигрыша игры делятся на: матричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др. Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Этот класс игр достаточно хорошо изучен. По характеру получения информации — на игры в нормальной форме (игроки получают всю информацию до начала игры) и динамические игры (информация поступает игрокам в процессе развития игры).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.252 (0.007 с.) |

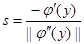 в однокритериальной задаче возможное подходящее направление.
в однокритериальной задаче возможное подходящее направление.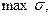
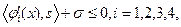
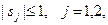
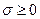
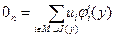
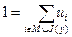
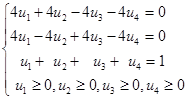 (2.15)
(2.15)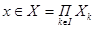 , i Î I ñ,
, i Î I ñ,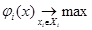 . Ясно, что величина выигрыша зависит от стратегий, выбранных другими игроками.
. Ясно, что величина выигрыша зависит от стратегий, выбранных другими игроками.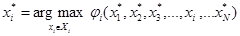 ,
,


