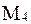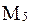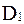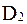Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений в условиях полной неопределенностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В условиях отсутствия дополнительной информации о вероятностях появления конкретных состояний природы используются следующие критерии: критерий максимакса (критерий крайнего оптимизма), максиминный критерий Вальда (критерий крайнего пессимизма), Сэвиджа, Гурвица (пессимизма-оптимизма). 1. Критерий максимакса. С помощью данного критерия определяется стратегия M= 2. Максиминный критерий Вальда. С позиции данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник (как игрок P2 в антагонистических играх). В этом случае игра становится антагонистической и наилучшей признается стратегия, на которой достигается нижняя цена игры: W= 3. Критерий минимаксного риска Сэвиджа. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей A, а матрицей рисков R: S= 4. Критерий пессимизма-оптимизма Гурвица. Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом. Согласно этому критерию, стратегия в матрице A выбирается в соответствии со значением
где p ( Отметим, что при p =0 критерий Гурвица совпадает с максимаксным критерием, а при p =1 – с критерием Вальда. Применительно к матрице рисков R критерий Гурвица имеет вид:
Принятие решений в условиях риска Будем считать, что для природы известны вероятности
Применительно к матрице рисков (матрице упущенных выгод) лучшей будет та стратегия игрока, которая обеспечивает ему минимальный средний риск:
Примеры
Пример 1. (Заготовка угля для обогрева дома) Необходимо закупить уголь для обогрева дома. Вторым игроком выступает природа – погодные условия зимой. Количество хранимого угля ограничено и в течение холодного периода должно быть полностью израсходовано. Предполагается, что неизрасходованный зимой уголь в лето пропадает. Покупать уголь можно в любое время, однако летом он дешевле, чем зимой. Неопределенность состоит в том, что неизвестно, какой будет зима: суровой, тогда придется докупать уголь, или мягкой, тогда часть угля может остаться неиспользованной. Имеются следующие данные о количествах и ценах угля, необходимого зимой для отопления.
Эти цены относятся к покупкам угля зимой. Летом цена угля 6 д.е. за 1 т., есть место для хранения запаса угля до 6 т., заготавливаемого летом. Если потребуется зимой докупить недостающее количество угля, докупка будет по зимним ценам. Предполагается, что весь уголь, который сохранится до конца зимы, в лето пропадает. Сколько угля летом покупать на зиму? Рассмотрим 2 случая: 1) вероятности наступления каждой из типов зим неизвестны (случай полной неопределенности); 2) известны наступления вероятности каждой зимы: для мягкой зимы – 0,35; для средней зимы – 0,5; холодной – 0,15. Решение 1) Построим матрицу выигрыша.
Для поиска стратегии игрока Р1, минимизирующего затраты в условиях полной неопределенности, воспользуемся каждым из перечисляемых выше критериев. 1. Критерий максимакса. Согласно данному критерию находим максимальный элемент матрицы выигрышей:
2. Максиминный критерий Вальда.
Следовательно, рекомендуется выбирать стратегию 3. Критерий минимаксного риска Сэвиджа. Построим матрицу риска R, используя матрицу A. Вычислим величины
Тогда S= Согласно данному критерию следует воспользоваться стратегией 4. Критерий Гурвица. Рассмотрим случай, когда коэффициент пессимизма равен 0,5. Тогда
= Отметим, что выбор конкретного критерия принятия решений зависит от субъективных особенностей Р1 (его склонности к риску). Однако, так как по 3 критериям из 4 лучшей оказалась первая стратегия, то эту стратегию и можно рекомендовать игроку. 2) Рассмотрим процедуру принятия решений в условиях риска. Для каждой чистой стратегии первого игрока рассмотрим математическое ожидание выигрыша при применении им данной стратегии, для чего составим таблицу.
Как видно из таблицы, наименьшая ожидаемая средняя плата приходится на случай закупки угля в размере 4 т., и по данному критерию первая стратегий Р1 является лучшей. Упражнения к § 4 №1. Для следующих игр с природой в условиях полной неопределенности, заданных матрицей игры A, построить матрицу риска и найти лучшие стратегии по каждому из критериев: критерий максимакса, Вальда, Сэвиджа, Гурвица (приняв p=0,5 и p=0,2), если: 1) 3) 4)
№ 2. Компания производит некоторую скоропортящуюся продукцию. Затраты на производство одного ящика продукции равны 45 д.е. Компания продает каждый ящик по цене 95 д.е. Если ящик с продукцией не продается в течение месяца, то она портится, и компания не получает дохода. Вероятности того, что спрос на продукцию в течение месяца будет 6, 7, 8 или 9 ящиков, равны соответственно 0,1; 0,3; 0,5; 0,1. Сколько ящиков следует производить в течение месяца?
№ 3. Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 7, 8, 9 или 10 бидонов, равны соответственно 0,2; 0,2; 0,5 и 0,1. Покупка одного бидона сметаны обходится магазину в 70 д.е., а продается сметана по цене 110 д.е. за бидон. Если сметана не продается в течение недели, она портится, и магазин несет убытки. Сколько бидонов сметаны желательно приобрести для продажи? Позиционые игры
Рассмотрим более сложные (позиционные, или многоэтапные) решения в условиях риска. Многие задачи, однако, требуют анализа последовательности решений и состояний среды, когда одна совокупность стратегий игрока и состояний природы порождает другое состояние подобного типа. Если имеют место два или более последовательных множества решений, причем последующие решения основываются на результатах предыдущих, и/или два или более множества состояний среды (т.е. появляется целая цепочка решений, вытекающих одно из другого, которые соответствуют событиям, происходящим с некоторой вероятностью), используется дерево решений. Дерево решений – это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды. Другое определение: деревья решений - это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение. Деревья решений разбивают данные на группы на основе значений переменных, в результате чего возникает иерархия операторов "ЕСЛИ - ТО", которые классифицируют данные. Под правилом понимается логическая конструкция вида «если - то». Узел – внутренний узел дерева, узел проверки. Лист – конечный узел дерева, узел решения. Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов. Этап 1. Формулирование задачи Прежде всего необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволит привести описание задачи принятия решения к поддающейся анализу форме. Должны быть выполнены следующие основные процедуры: определение возможностей сбора информаций для экспериментирования и реальных действии; составление перечня событии, которые с определенной вероятностью могут произойти; установление временного порядка расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, которые можно предпринять. Этап 2. Построение дерева решений Этап 3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события. Следует отметить, что указанные вероятности определяются либо на основании имеющейся статистики, либо экспертным путем. Этап 4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды. Этап 5. Решение задачи. Рисуют деревья слева направо. Места, где принимаются решения, обозначают квадратами, места появления исходов – кругами, возможные решения – пунктирными линиями, возможные исходы – сплошными линиями. Для каждой альтернативы рассчитывается ожидаемая стоимостная оценка (EMV) – как максимальная из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов (см. пример). Пример. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий: а). Построить большой завод стоимостью Ст1 = 500 тысяч у.е. При этом варианте возможны большой спрос (годовой доход в размере Д1 = 200 тысяч у.е. в течение следующих 5 лет) с вероятностью p1 = 0,7 и низкий спрос (ежегодные убытки Д2 = 90 тысяч у.е.) с вероятностью р2 = 0,3. б). Построить маленький завод стоимостью Ст2 = 300 тысяч у.е. При этом варианте возможны большой спрос (годовой доход в размере Д3 = 100 тысяч у.е. в течение следующих 5 лет) с вероятностью p3 = 0,7 и низкий спрос (ежегодные убытки Д4 = 40 тысяч у.е.) с вероятностью р4 = 0,3. в). Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p5 = 0,4 и p6 = 0,6 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p7 = 0,8 и р8 = 0,2 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет. Нарисовав дерево решений, определим наиболее эффективную последовательность действий, основываясь на ожидаемых доходах. Решение. Строим дерево решений. Строим узел 1, из которого исходят три заявленные в условии варианты. Обозначаем эти ветви пунктиром, поскольку это – возможные решения. На концах ветвей ставим узлы-исходы, заключаем их в круг и обозначаем буквами А, В и т.д. Рисуем из этих узлов-исходов ветви с возможными исходами при выборе того или иного варианта из условия. Под каждой ветвью подписываем вероятности соответствующих исходов. На концах каждой ветви, не закрытой новым узлом, выставляем доходы и убытки, умноженные (исходя из условия) на время (годы из условия). На ветвях (возможные решения) ставим стоимость строительства со знаком «-», так как это расходы компании. Убытки на концах «открытых» ветвей также пишем со знаком «-» (рис.3).
Рис.3 – Дерево решений для примера 1. Первый этап построения
Далее считаем ожидаемые стоимостные оценки узлов. Ожидаемая стоимостная оценка узла А равна: ЕМV(А) = 0,8 х 1000 + 0,2 х (-450) -500 = 210. EMV(B) = 0,8 х 500 + 0,2 х (-200) - 300 = 60. EMV(D) = 0,9 x 800 + 0,1 x (-360) - 500 = 184. EMV(E) = 0,9 x 400 + 0,1 х (-160) - 300 = 44. Для узлов принятия решения 2 (второй уровень, условно) выбираем максимальную оценку: EMV(2) = max {EMV(D), EMV(E)} = max {184, 44} = 184 = EMV(D). Поэтому в узле 2 отбрасываем возможное решение «маленький завод». EMV(C) = 0,7 x 184 + 0,3 x 0 = 128,8. Для узла принятия решения 1 – узла принятия окончательного решения, аналогично выбираем максимальную оценку на других узлах. EMV(1) = max {ЕМV(A), EMV(B), EMV(C)} = max {210; 60; 128,8} = 210 = =EMV(А). Поэтому в узле 1 выбираем решение «большой завод». Исследование проводить не нужно. Строим большой завод. Ожидаемая стоимостная оценка этого наилучшего решения равна 210 тысяч у.е.(рис.4). Ответ: наиболее подходящее решение – решение строить большой завод.
Рис.4 – Дерево решений со стоимостными оценками
В рассмотренном примере мы произвели отсечение ветвей в узле 2. И далее в задаче мы отсекаем те ветви и узлы, стоимостные оценки которых не приемлемы для принятия наиболее выгодного решения. Упражнения 1. Предположим, у вас имеется возможность вложить деньги либо в 7,5%-ные облигации, которые продаются по номинальной цене, либо в специальные фонды, которые выплачивает лишь 1% дивидендов. Если существует вероятность инфляции, процентная ставка возрастает до 8%, и в этом случае номинальная стоимость облигаций увеличивается на 10%, а цена акций фонда – на 20%. Если прогнозируется спад, то процентная ставка понизится до 6%. При этих условиях ожидается, что номинальная стоимость облигаций поднимется на 5%, а цена акций фонда – на 20%. Если состояние экономики останется неизменным, цена акций фонда увеличится на 8%, а номинальная стоимость облигаций не изменится. Экономисты оценивают в 20% шансы наступления инфляции и в 15% - наступление спада. Ваше решение относительно инвестиций принимается с учетом экономических условий следующего года. А) Представьте данную задачу в виде дерева решений. Б) Будете ли вы покупать акции фонда или облигации?
2. Фирма планирует производство новой продукции быстрого питания в национальном масштабе. Исследовательский отдел убежден в большом успехе новой продукции и хочет внедрить её немедленно, без рекламной компании на рынках сбыта фирмы. Отдел маркетинга положение вещей оценивает иначе и предлагает провести интенсивную рекламную компанию. Такая компания обойдется в 100000 долл., а в случае успеха принесет 950000 долл. годового дохода. В случае провала рекламной компании (вероятность этого составляет 30%) годовой доход оценивается лишь в 200000 долл. Если рекламную компанию не проводить вовсе, годовой доход оценивается в 400000 долл. при условии, сто покупателям понравится новая продукция (вероятность этого равна 0,8), и в 200000 долл. с вероятностью 0,2, если покупатели останутся равнодушными к новой продукции. А) Постройте соответствующее дерево решений. Б) Как должна поступить фирма в связи с производством новой продукции?
3. Торговая фирма-поставщик строительных материалов, не имеющая лицензии на импорт товаров, получила предложение от зарубежной фирмы на поставку 100000 единиц высококачественных строительных материалов по цене 5 дол. за единицу. Средняя цена продажи на внутреннем рынке составляет 8 дол. за единицу. Вероятность отказа государственных органов в выдаче лицензии на внешнеторговую деятельность составляет 0,5. Если фирма будет ожидать соответствующего решения, то она с вероятностью 0,7 может потерять возможность совершения сделки, так как контракт может быть перехвачен конкурентами. Если же контракт будет заключен, а в лицензии будет отказано, то фирме придется уплатить неустойку в размере 100000 дол. Существует также возможность обратиться за помощью к консультанту, который может быстро подготовить рекомендации о целесообразности заключения данной сделки с учетом ожидаемых действий государственных органов. Расходы по оплате консалтинговых услуг составляют 1000 дол. Вероятность получения лицензии при положительной оценке консультанта составит 0,8, а при отрицательной - 0,05. При этом вероятность получения положительной оценки эксперта-консультанта составляет 0,6. Требуется разработать стратегию деятельности фирмы по заключению контракта. Задания для самостоятельной работы Примечание: для обеспечения индивидуального варианта решения к данным, помеченным * прибавляется два последних числа из номера зачетной книжки. Если исходные данные представлены в виде десятичной дроби, то изменяется дробная часть. Например, номер зачетной книжки имеет вид хххххх 53, исходные данные задачи принимают значение 1000*=1000+53=1053 или 0,2*=0,2+0,53=0,73. Если по условию задачи требуется значение параметра из интеравала Задача 1. (планирование выпуска побочной продукции). В городе имеются 2 предприятия, которые, помимо своих основных изделий, могут выпускать для населения побочную продукцию одного и того же назначения, но разных типов. Первое предприятие может выпускать продукцию типов
Требуется определить количество игрушек каждого типа, выпускаемого каждым предприятием.
Задача 2. Администрации театра нужно решить, сколько заказать программок для представлений. Стоимость заказа 200 ф. ст. (GBP) плюс 30 пенсов за штуку. Программки продаются по 60 пенсов за штуку, и к тому же доход от рекламы составит дополнительные 300 GBP. Из прошлого опыта известна посещаемость театра.
Ожидается, что 40% зрителей купят программки. 1. Определите, сколько программок должна заказать администрация театра. 2. Допустим, что рекламодатели увеличат сумму с 300 до 400 GBP., число посетителей будет больше 5250*, к тому же спрос на программки будет полностью удовлетворен. Как это повлияет на рекомендации в п. 1? Задача 3. Вы рассматриваете перспективы создания новой консалтинговой службы. Объем необходимых вложений на начальном этапе 200 тыс. дол. Существует 60%- ная вероятность, что спрос будет высоким в 1-й год. Если спрос будет высоким в первый год, то в последующие годы вероятности высокого и низкого спроса составят 80% и 20% соответственно. Если спрос будет низким в 1-й год, то в последующие годы вероятности высокого и низкого спроса составят 40% и 60% соответственно. При высоком спросе прогнозируемые доходы составят 500* тыс. дол. в год; при низком спросе прогнозируемые доходы равны 300* тыс. дол. в год. Вы можете прекратить предоставлять услуги в любой момент. Затраты, помимо связанных с использованием компьютера, прогнозируются в размере 140* тыс. дол. в год, вне зависимости от уровня спроса. Если Вы решите не вкладывать деньги в консалтинговую службу, то сможете вложить их на практически безрисковой основе под 20% в год. Если будет решено организовать консалтинговую службу, Вам необходимо будет решить вопрос с проведением компьютерных расчетов, составляющих основу деятельности. Один возможный вариант - купить сервер. Срок морального устаревания его 5 лет. Затраты будут состоять из первоначальных расходов в размере 150* тыс. дол. и ежегодных расходов на эксплуатацию в размере 20* тыс. Альтернативный вариант — арендовать компьютерные ресурсы по мере необходимости. В этом случае затраты на аренду будут пропорциональны спросу и составят 30 % доходной части за вычетом оговоренных постоянных расходов в 140* тыс. Во всех случаях никаких других издержек нет. 1) Постройте дерево решений, иллюстрирующее эти варианты и охватывающее 3 года. 2) Стоит организовать консалтинговую службу или безрисковый доход выгоднее? Рассмотрите итоги деятельности за два и три года. 3) Что лучше — купить компьютер или арендовать? 4) Предположим, что после 3 лет деятельности вы сможете продать службу, как отдельный бизнес в среднем за 350* тыс. дол. Какому ежегодному проценту прироста соответствует полученный вами доход? 5) Четко сформулируйте любые дополнительные допущения, которые вам потребуется сделать.
СПИСОК ЛИТЕРАТУРЫ I. Основная литература
1. Бондаренко Ю.В. Механизмы принятия решений по регулированию социально-экономической системы региона: монография / Ю.В. Бондаренко. – Воронеж: Издательство «Научная книга», 2013. – 156 с. 2. Васин А.А. Теория игр и модели математической экономики / А.А. Васин, В.В. Морозов. – М.: МАКС Пресс, 2005. – 272 с. 3. Дубина И.Н. Основы теории экономических игр: учеб. пособие / И.Н. Дубина. – М.: КНОРУС, 2010. – 208 с. 4. Колокольцов В.Н. Математическое моделирование многоагентных систем конкуренции и кооперации (Теория игр для всех): учеб. пособие / В.Н. Колокольцов, О.А. Малафеев. – СПб.: Изд-во «Лань», 2012. – 624 с. 5. Новиков Д.А. Рефлексивные игры / Д.А. Новиков, А.Г. Чхартишвили. – М.: СИНТЕГ,2003. – 160 с. 6. Оуэн Г. Теория игр / Г. Оуэн. – М.: Вузовская книга, 2007. – 216 с. 7. Петросян Л.А. Теория игр / Л.А. Петросян, Н.А. Зенкевич, Е.А. Семина. – М.: Высш. шк., 1998. – 304 с. 8. Угольницкий Г.А. Модели конфликтов: учеб. пособие / Г.А. Угольницкий. – М.: Вузовская книга, 2012. – 320 с. 9. Харшаньи Дж. Общая теория выбора равновесия в играх / Дж. Харшаньи, Р. Зельтен. – СПб.: Экономическая школа,2001. – 424 с.
II. Дополнительная литература 1. Воробьев Н.Н. теория игр для экономистов-кибернетиков / Н.Н. Воробьев.– М.: Наука, 1985. – 427 с. 2. Гермейер Ю.Б. Игры с непротивоположными интересами/ Ю.Б. Гермейер. – М.: Наука, 1976. – 328 с. 3. Дюбин Г.Н. Введение в прикладную теорию игр/ Г.Н. Дюбин, В.Г. Суздаль. – М.: Наука,1981. – 328 с. 4. Карлин С. Математические методы в теории игр, программировании, экономике/ С. Карлин. – М.: Мир, 1964. - 838 с. 5. Мулен Э. Теория игр с примерами из математической экономики/ Э. Мулен. – М.: Мир,1985. – 200 с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1874; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.231.160 (0.012 с.) |

 , применяя которую, игрок при благоприятном стечении обстоятельств может получить максимально возможный выигрыш:
, применяя которую, игрок при благоприятном стечении обстоятельств может получить максимально возможный выигрыш: .
. .
. .
. ,
, ) – коэффициент пессимизма.
) – коэффициент пессимизма. .
. появления состояния
появления состояния  , задаваемые, например, экспертно. В этом случае лучшей стратегией игрока 1 будет та, которая обеспечивает ему максимальный средний выигрыш, то есть
, задаваемые, например, экспертно. В этом случае лучшей стратегией игрока 1 будет та, которая обеспечивает ему максимальный средний выигрыш, то есть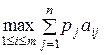 .
. .
. Зима
Количество угля
Зима
Количество угля
 . Следовательно, первому игроку рекомендуется выбрать свою первую стратегию
. Следовательно, первому игроку рекомендуется выбрать свою первую стратегию 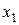 (4 т.).
(4 т.).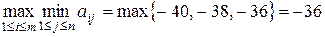 .
. (6 т.).
(6 т.). :
: 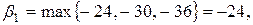


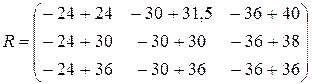 =
=  .
.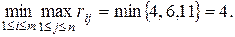
 =
= . Следовательно, первому игроку рекомендуется выбрать свою первую стратегию
. Следовательно, первому игроку рекомендуется выбрать свою первую стратегию 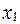 (4 т.).
(4 т.). Зима
Количество
Зима
Количество
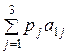 = 0,35(-24)+ 0,5(-31,5) + 0,15(-40) =
=-30,15
= 0,35(-24)+ 0,5(-31,5) + 0,15(-40) =
=-30,15
 = 0,35(-30) + 0,5(-30) + 0,15(-38)=
=-31,2
= 0,35(-30) + 0,5(-30) + 0,15(-38)=
=-31,2
 =- 36
=- 36
 ; 2)
; 2) 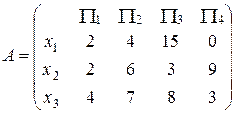 ;
; ;
; .
.

 , а в результате при изменении дробной части получается число больше 1, целая часть числа отбрасывается.
, а в результате при изменении дробной части получается число больше 1, целая часть числа отбрасывается. , а второе – типов
, а второе – типов  . В городе найдет сбыт 1000* единиц товара всех видов. Прогнозируемая доля сбыта продукции первым предприятием задана таблицей.
. В городе найдет сбыт 1000* единиц товара всех видов. Прогнозируемая доля сбыта продукции первым предприятием задана таблицей.