
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие игры. Классификация игрСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теорией игр называется математическая теория принятия оптимальных решений в конфликтных ситуациях. Поясним это определение. Простейшие модели принятия решений рассматриваются в курсах математического анализа и оптимизации. В этих моделях лицо, принимающее решение (ЛПР), выбирает свое действие из некоторого множества стратегий. Считается, что задана целевая функция, которая отражает интересы ЛПР и зависит от выбранной им стратегии. Задача принятия решений в такой постановке состоит, как правило, в том, чтобы найти стратегию, доставляющую максимум целевой функции. Отличие конфликтной ситуации заключается в том, что решения принимаются не одним индивидуумом, а несколькими участниками, и функция выигрыша каждого индивидуума зависит не только от его стратегии, но также и от решения других участников. Математическая модель такого рода конфликта называется игрой, а участники конфликта – игроками. Таким образом, игра – это идеализированная математическая модель коллективного поведения: несколько индивидуумов (участников, игроков) влияют на ситуацию, причем их интересы (выигрыши при различных возможных ситуациях) различны.
Игры можно классифицировать по следующим признакам:
1. По возможности ведения игроками предварительных переговоров игры делятся на: 1) бескоалиционные игры (игроки действуют самостоятельно, независимо друг от друга, и если какие-то соглашения заключаются, то они не являются обязывающими); 2) кооперативные (коалиционные) игры (игроки объединяются в коалиции в предположении, что существует механизм, обеспечивающий выполнение совместного принятого решения).
2. По свойствам выигрыша различают: 1) антагонистические игры (выигрыш одного игрока равен проигрышу второго); 2) неантагонистические (с ненулевой суммой) игры.
3. По характеру получения информации выделяют: 1) игры в нормальной форме (игроки получают информацию до начала игры); 2) динамические игры (игроки получают информацию в процессе развития игры). 4. По числу стратегий игры делятся на: 1) конечные (множество стратегий каждого из игроков конечно); 2) бесконечные (множество стратегий хотя бы одного из игроков бесконечно).
Антагонистические игры в нормальной форме
Определение антагонистической игры в нормальной форме. Матричные игры Рассмотрим игру, в которой принимают участие два игрока – P1 и Р2. Первый игрок выбирать любое действие (стратегию, чистую стратегию) x из множества допустимых стратегий X, а второй игрок соответственно стратегию y из множества Y. Пара Для каждого игрока задана функция выигрыша Полагаем, что каждый игрок знает до начала игры информацию о множествах стратегий и функциях выигрыша.
Определение 1. Система
Определение 2. Антагонистическая игра, в которой множества стратегий игроков являются конечными множествами, называется матричной игрой.
Пусть m – количество стратегий игрока 1, тогда Примеры
Пример 1. Рассмотрим следующую игру. Игроки выбирают одновременно одно из трех чисел: «один», «два», «три». Выигрыш Р1 (проигрыш Р2) положителен и равен названному числу, если он правильно угадал выбор второго игрока и 0 в противном случае.
В данной задаче
Пример 2. Оборона города (игра полковника Блотто). Полковник Блотто (игрок Р1) имеет 4 полка, а его противник (Р2) – 3 полка. Противник защищает 2 позиции. Позиция будет занята полковником Блотто, если на ней наступающие полки окажутся в численном превосходстве. При этом, если у полковника Блотто на позиции полков больше, чем у противника, то его выигрыш на этой позиции равен числу полков противника плюс один (за захват позиции). Если у Р2 полков больше, то Р1 теряет все свои полки и 1 за позицию.
Если число полков Р1 и Р2 на позиции одинаково, то имеет место ничья и никто ничего не получает. Считая, что суммарный выигрыш Р1 равен сумме его выигрышей по двум позициям и игра является антагонистической, сформировать матрицу игры.
Решение Стратегией первого игрока является пара
Рассмотрим формирование элементов матрицы на примере
3.2 Ситуация равновесия в чистых стратегиях: понятие и существование
Рассмотрим антагонистическую игру В теории игр предполагается, что оба игрока ведут себя рационально, то есть стремятся получить максимально возможную величину гарантированного выигрыша. Пусть игрок 1 выбрал стратегию
Замечание 1. Для матричной игры
Лемма 1. Для любой антагонистической игры
Рассмотрим вопрос оптимального поведения игроков. Ситуация
Определение 3. В антагонистической игре
Так как
Замечание 2. В матричной игре ситуация
Свойства ситуаций равновесия Пусть 1) 2) Необходимые и достаточные условия существования ситуации равновесия в чистых стратегиях доказываются следующей теоремой.
Теорема 1. Для того, чтобы в игре
и выполнялось равенство: Доказательство 1. Необходимость. Пусть По определению ситуации равновесия:
Тогда Так как
Аналогично:
Из (*), (**) следует: 2. Достаточность. Пусть существуют Пусть
Докажем, что
Тогда, так как правые части неравенств равны по условию, то
В случае если верхняя цена игры и нижняя совпадают, величину Для антагонистической игры справедлива следующая лемма о масштабе.
Лемма 2. (Лемма о масштабе) Пусть
Примеры Пример 1. Найти верхнюю и нижнюю цены игры и ситуацию равновесия, при условии, что она существует, если матрица имеет вид:
Решение Найдем нижнюю цену игры. Если Р1 выберет первую стратегию, то он получит гарантированно Если Р1 выберет стратегию 2, то он получит гарантированно Если Р1 выберет стратегию 3, то он получит гарантированно Тогда выбором своей стратегии Р1 может получить, по крайней мере не меньше Найдем верхнюю цену игры. Если Р2 выберет первую стратегию, то он проиграет гарантированно не больше Если Р2 выберет стратегию 2, то он проиграет гарантированно не больше Если Р2 выберет стратегию 3, то он проиграет гарантированно не больше Тогда выбором своей стратегии Р2 может проиграть, по крайней мере, не меньше
Пример 2. Пусть дана матрица выигрышей игрока P1 Решение В данной игре
Упражнения к § 3.1. – 3.2
№ 1. Найдите верхнюю, нижнюю цену игры, ситуации равновесия (если они существуют) для игр, заданных следующими матрицами: 1) 4)
№ 2. В игре Морра с тремя пальцами каждый игрок показывает 1, 2 или 3 пальца одновременно, называя число пальцев, которые покажет его оппонент. Выигрывает тот, кто правильно назовет число пальцев, показанных противником. Выигрыш равен сумме пальцев, показанных обоими игроками. Написать матрицу игры и показать, что она не имеет ситуации равновесия.
№ 3. Каждый из двух игроков имеет n рублей. Они хотят получить некоторый предмет стоимостью C>0. Каждый дает за него i рублей (
№ 4. (Дискретная игра типа дуэли). Игроки продвигаются навстречу друг другу на n шагов одновременно. После каждого сделанного шага игрок может выстрелить или нет, но во время игры он может выстрелить только один раз. Считается, что вероятность того, что игрок попадет в своего противника, если выстрелит, продвинувшись на k шагов, равна
№ 5. В системе ПВО объекта могут применяться 3 типа средств поражения воздушной цели (1, 2, 3), которые должны быть распределены между двумя стартовыми установками. У противника (P2) имеется 2 типа самолетов (тип 1, тип 2). Вероятности поражения самолета одним средством сведены в таблицу
Предполагается, что возможно нападение только одним из самолетов. Выигрыш первого игрока равен вероятности поражения самолета системой ПВО. Построить матрицу игры и выяснить, имеет ли игра решение в чистых стратегиях.
№ 6. На каждой из двух торговых баз ассортиментный минимум составляет один и тот же набор из n видов товаров. Каждая база должна поставить в свой магазин только один из этих видов товара. Магазины, обозначим их A и B, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако, товар, поставляемый в магазин B, более высокого качества. Если магазин A завезет с базы товар i -го вида
Требуется формализовать данную конфликтную ситуацию и построить матрицу игры при n=3.
№ 7. Торговый агент должен встретиться с иногородним клиентом и собирается лично вручить ему заказ на 3000 у.д.ед. Если агент поедет поездом, то потеряет день на работе, который принес бы ему 1500 у.д.ед. Полет самолетом позволит сократить рабочий день, но если самолет не полетит из-за тумана, то личная встреча с клиентом не состоится и день на работе не будет потерян. В этом случае придется говорить с клиентом по телефону, что уменьшит сумму заказа до 500 у.д.ед. Вероятность тумана оценивается как 0,1. Требуется формализовать данную конфликтную ситуацию и построить матрицу игры.
№ 8. Фирма А производит некоторый сезонный товар, имеющий спрос в течение n единиц времени, и который она может поставить на рынок в один из моментов i Для конкурентной борьбы с фирмой А дочерняя фирма В концерна D, не заботясь о собственных доходах, производит аналогичный товар, который поступает на рынок в один из моментов j Требуется построить функцию выигрыша фирмы А, где под выигрышем понимается доход этой фирмы, зависящий от складывающихся ситуаций. Используя функцию выигрыша, составить матрицу игры для случая n =4 и выписать конкретный вид этой матрицы, который она приобретает в случае, когда доход с =6 денежным единицам.
3.3 Смешанное расширение игры
Если игра не имеет ситуации равновесия в чистых стратегиях, то игроки, применяя свои максиминную и минимаксную чистые стратегии, создают неустойчивую ситуацию, которую один из игроков может изменить с выгодой для себя. С другой стороны, представляется, что ничего другого осторожным игрокам рекомендовать нельзя. И все-таки из этого положения есть выход. Каждый из игроков может выбирать свои чистые стратегии случайно, то есть может определить распределение вероятностей на множестве чистых стратегий, а затем предоставить выбор конкретной чистой стратегии случайному механизму. Выбор игроками своих чистых стратегий с некоторыми заранее заданными вероятностями – по существу один из планов проведения игры и в этом смысле тоже является некоторой стратегией. В отличие от первоначально заданных (чистых), такие стратегии называются смешанными. Рассмотрим матричную игру
Пусть При выборе смешанной стратегии игроки руководствуются критерием максимизации математического ожидания своего выигрыша. Отсутствие обмена информацией между игроками делает их случайные выборы своих чистых стратегий независимыми. Поэтому, если они применяют свои смешанные стратегии
Определение 4. Тройка
Определение 5. Решением смешанного расширения матричной игры
Для смешанного расширения игры
Лемма 3. Пусть
Сформулируем несколько теорем, представляющих свойства оптимальных смешанных стратегий в антагонистической игре, используя которые в дальнейшем (п. 2.5), сможем доказать теорему о существовании ситуации равновесия в смешанных стратегиях.
Свойства оптимальных стратегий и цены смешанного расширения игры 1. Пусть
2. Пусть
При этом
3. Для матричной игры
4. Для того чтобы ситуация
5. Пусть Приведем доказательство свойства 2 оптимальных стратегий.
Доказательство свойства 2 1. Необходимость. Пусть
для всех
2. Достаточность. Пусть
Пусть
а из правой части (*)
При этом имеем:
Подставляя данные равенства в (**) и учитывая произвольность стратегий x и y, получаем равновесность ситуации Свойство доказано.
3.4 Методы решения матричных игр
Рассмотрим методы решения матричных игр, основанные на использовании свойств оптимальных стратегий.
1. Сведение игры к системе неравенств
Свойство 2 оптимальных стратегий означает, что любая матричная игра может быть сведена к системе уравнений и неравенств. Пусть
Решением системы двух уравнений и m+n неравенств, содержащих m+n+1 переменную, являются оптимальные стратегии игроков В случае, если размерность задач оказывается достаточно небольшой, возможно найти решение системы, заменив неравенства уравнениями. Рассмотрим следующий пример. Примеры Пример 1. Найти цену и оптимальные стратегии игроков в игре с матрицей Решение Пусть
Заменяя системы уравнений и неравенств равенствами и решая полученную систему линейных уравнений, получаем значения искомых величин:
2. Графический (графоаналитический) метод решения игры
Если число стратегий хотя бы одного из игроков равна 2, то оптимальную стратегию этого игрока и оптимальное значение цены игры возможно найти графическим методом, используя свойство 3 оптимальных стратегий:
1. Рассмотрим игру, в которой игрок 1 имеет две стратегии, а игрок 2 имеет n стратегий. Матрица игры в этом случае представима в виде:
Пусть игрок 1 выбрал смешанную стратегию
Геометрически оно представляет собой прямую в координатах
является нижняя огибающая семейства прямых (3). Точка
Примеры Пример 2. Рассмотрим игру с матрицей Для каждого
Нижняя огибающая Максимум | |||||||||||||||||||
|
| Поделиться: |

 называется ситуацией (а также в дальнейшем ситуацией в чистых стратегиях).
называется ситуацией (а также в дальнейшем ситуацией в чистых стратегиях).
 ставящая в соответствие каждой ситуации (x,y) величину выигрыша i -го игрока
ставящая в соответствие каждой ситуации (x,y) величину выигрыша i -го игрока  , полученную в данной ситуации. При этом будем считать, что интересы игроков противоположны, то есть выигрыш первого игрока равен проигрышу второго. Тогда функцию выигрыша первого игрока (проигрыша второго) будем обозначать как
, полученную в данной ситуации. При этом будем считать, что интересы игроков противоположны, то есть выигрыш первого игрока равен проигрышу второго. Тогда функцию выигрыша первого игрока (проигрыша второго) будем обозначать как 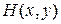 , где
, где  .
. , где X, Y – непустые множества стратегий первого и второго игроков соответственно,
, где X, Y – непустые множества стратегий первого и второго игроков соответственно,  – функция выигрыша первого игрока (проигрыша второго), называется антагонистической игрой в нормальной форме (игрой с нулевой суммой).
– функция выигрыша первого игрока (проигрыша второго), называется антагонистической игрой в нормальной форме (игрой с нулевой суммой). . Аналогично, n – число стратегий P2,
. Аналогично, n – число стратегий P2,  . В этом случае
. В этом случае  однозначно определяется заданием матрицы
однозначно определяется заданием матрицы 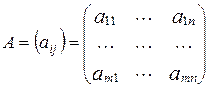 , где
, где  – величина выигрыша P1 (проигрыша Р2) при условии, что Р1 выбрал стратегию
– величина выигрыша P1 (проигрыша Р2) при условии, что Р1 выбрал стратегию  а Р2 стратегию
а Р2 стратегию 
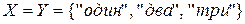 , а матрица игры имеет следующий вид:
, а матрица игры имеет следующий вид:
 .
. ,
, 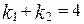 , где
, где  – число полков, отправленных Блотто на позицию 1,
– число полков, отправленных Блотто на позицию 1,  – на позицию 2. Тогда
– на позицию 2. Тогда  . Аналогично для второго игрока
. Аналогично для второго игрока  . Матрица игры имеет следующий вид:
. Матрица игры имеет следующий вид: .
. – величины выигрыша Р1 при условии, что он предпринял стратегию (4,0), а второй игрок стратегию (1,2). На первой позиции полки полковника Блотто оказываются в численном превосходстве (4>1), поэтому он выигрывает число полков противника (1) плюс 1 за захват позиции (всего выигрыш по позиции равен 2). На второй позиции наоборот, полки Р2 оказываются в превосходстве (0<2) и тогда Блотто теряет все свои полки на этой позиции (0) и 1 за поражение на позиции (всего выигрыш по позиции равен -1). Суммарный выигрыш Блотто по двум позициям:
– величины выигрыша Р1 при условии, что он предпринял стратегию (4,0), а второй игрок стратегию (1,2). На первой позиции полки полковника Блотто оказываются в численном превосходстве (4>1), поэтому он выигрывает число полков противника (1) плюс 1 за захват позиции (всего выигрыш по позиции равен 2). На второй позиции наоборот, полки Р2 оказываются в превосходстве (0<2) и тогда Блотто теряет все свои полки на этой позиции (0) и 1 за поражение на позиции (всего выигрыш по позиции равен -1). Суммарный выигрыш Блотто по двум позициям:  . Аналогично формируются остальные элементы матрицы.
. Аналогично формируются остальные элементы матрицы. . Каждый из игроков выбором стратегии стремится максимизировать свой выигрыш, который для Р1 определяется величиной
. Каждый из игроков выбором стратегии стремится максимизировать свой выигрыш, который для Р1 определяется величиной  , а для второго игрока величиной
, а для второго игрока величиной  . Выигрыши игроков определены на ситуациях
. Выигрыши игроков определены на ситуациях  и поэтому в своем поведении каждый игрок должен учитывать поведение противника.
и поэтому в своем поведении каждый игрок должен учитывать поведение противника. . Р1 может себе гарантировать получение, по крайней мере, величины выигрыша
. Р1 может себе гарантировать получение, по крайней мере, величины выигрыша 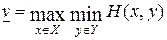 , которая называется нижней ценой игры или максимином. С другой стороны, игрок 2 может себе гарантировать величину проигрыша не меньшую, чем
, которая называется нижней ценой игры или максимином. С другой стороны, игрок 2 может себе гарантировать величину проигрыша не меньшую, чем  , называемую верхней ценой игры или минимаксом.
, называемую верхней ценой игры или минимаксом.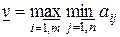 ,
,  .
. .
. называется равновесной в игре
называется равновесной в игре  и второму игроку от стратегии
и второму игроку от стратегии 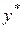 при условии, что противник придерживается равновесной стратегии.
при условии, что противник придерживается равновесной стратегии. называется ситуацией равновесия или седловой точкой, если выполнены следующие неравенства:
называется ситуацией равновесия или седловой точкой, если выполнены следующие неравенства: , для всех стратегий
, для всех стратегий  ,
, 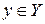 .
. , то при условии, что второй игрок выбрал стратегию
, то при условии, что второй игрок выбрал стратегию  , так как при этом его выигрыш не увеличится. Аналогично, используя правую часть неравенства (1), приходим к выводу, что отклонение от
, так как при этом его выигрыш не увеличится. Аналогично, используя правую часть неравенства (1), приходим к выводу, что отклонение от  невыгодно P2.
невыгодно P2. называется ситуацией равновесия или седловой точкой матрицы А, если выполняются неравенства:
называется ситуацией равновесия или седловой точкой матрицы А, если выполняются неравенства:  ,
,  ,
,  . Другими словами, элемент
. Другими словами, элемент  является одновременно минимумом в строке
является одновременно минимумом в строке  и максимумом в столбце
и максимумом в столбце  .
. ,
,  – ситуации равновесия в антагонистической игре
– ситуации равновесия в антагонистической игре  ;
; ,
,  – ситуации равновесия.
– ситуации равновесия. ,
, .
. – ситуация равновесия. Докажем, что
– ситуация равновесия. Докажем, что  , и поэтому достаточно показать выполнение неравенства
, и поэтому достаточно показать выполнение неравенства 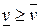 .
. ,
, 
 .
. , а следовательно,
, а следовательно,  .
. , то
, то . (*)
. (*) . (**)
. (**) , что и требовалось доказать.
, что и требовалось доказать. ,
,  и выполнено равенство
и выполнено равенство  и
и  ;
; и
и 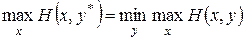 .
. – ситуация равновесия.
– ситуация равновесия. ;
; .
. ,
, и
и ,
,  , что и требовалось доказать.
, что и требовалось доказать. называют ценой игры.
называют ценой игры. – две антагонистические игры, причем
– две антагонистические игры, причем 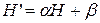 , где
, где  ,
,  – некоторые константы. Тогда множества оптимальных стратегий игроков в
– некоторые константы. Тогда множества оптимальных стратегий игроков в  совпадают, а
совпадают, а  .
. .
. .
. .
. .
. .
. .
. .
. .
. . Так как
. Так как  =1, то равновесием является пара
=1, то равновесием является пара  и v= 1.
и v= 1. . Найти ситуации равновесия.
. Найти ситуации равновесия. ,
,  , и поэтому игра не имеет ситуации равновесия. Если игрок P1 выбирает свою чистую максиминную стратегию
, и поэтому игра не имеет ситуации равновесия. Если игрок P1 выбирает свою чистую максиминную стратегию  , то игрок P2, выбрав свою минимаксную стратегию
, то игрок P2, выбрав свою минимаксную стратегию  , проигрывает только 20 единиц. В этом случае P1 выгодно выбрать стратегию
, проигрывает только 20 единиц. В этом случае P1 выгодно выбрать стратегию  , то есть отклониться от своей максиминной стратегии и выиграть 30. Тогда P2 будет выгодно отклониться от своей чистой минимаксной стратегии и проиграть 10. В свою очередь, игрок P1 должен выбрать свою 2-ю стратегию, чтобы выиграть 40, а P2 ответит выбором 2-й стратегии и т. д.
, то есть отклониться от своей максиминной стратегии и выиграть 30. Тогда P2 будет выгодно отклониться от своей чистой минимаксной стратегии и проиграть 10. В свою очередь, игрок P1 должен выбрать свою 2-ю стратегию, чтобы выиграть 40, а P2 ответит выбором 2-й стратегии и т. д. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  .
. ) так, чтобы другой не знал, сколько дал первый. Тот, кто предложил больше денег, получает предмет и выплачивает другому игроку ту сумму, которую он сам предлагал. Если оба игрока давали одинаковую цену, то предмет без всякой компенсации отдается одному из партнеров – это решается бросанием монеты. Тогда каждый имеет ожидаемую долю
) так, чтобы другой не знал, сколько дал первый. Тот, кто предложил больше денег, получает предмет и выплачивает другому игроку ту сумму, которую он сам предлагал. Если оба игрока давали одинаковую цену, то предмет без всякой компенсации отдается одному из партнеров – это решается бросанием монеты. Тогда каждый имеет ожидаемую долю  в этом предмете. Напишите матрицу выигрыша и определите, имеет ли она седловую точку.
в этом предмете. Напишите матрицу выигрыша и определите, имеет ли она седловую точку. (
( ). Стратегия каждого игрока – принять решение стрелять на i-ом (j-ом) шаге. Выигрыш P1 равен разности вероятностей того, что он попадет в противника, и того, что попадут в него. Написать матрицу игры. Имеются ли ситуации равновесия?
). Стратегия каждого игрока – принять решение стрелять на i-ом (j-ом) шаге. Выигрыш P1 равен разности вероятностей того, что он попадет в противника, и того, что попадут в него. Написать матрицу игры. Имеются ли ситуации равновесия? , отличный от товара j -го вида
, отличный от товара j -го вида  , завезенного в магазин B, то товар i- го вида будет пользоваться спросом и магазин A получит прибыль
, завезенного в магазин B, то товар i- го вида будет пользоваться спросом и магазин A получит прибыль 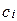 денежных единиц. Если же в магазины A и B завезены товары одинакового вида i=j, то товар i -го вида в магазине A спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества можно купить в магазине B, и поэтому магазин A понесет убытки по транспортировке, хранению и, возможно, порче товара i -го вида в размере
денежных единиц. Если же в магазины A и B завезены товары одинакового вида i=j, то товар i -го вида в магазине A спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества можно купить в магазине B, и поэтому магазин A понесет убытки по транспортировке, хранению и, возможно, порче товара i -го вида в размере  денежных единиц.
денежных единиц. . Цель фирмы В – разорение фирмы А, после чего, используя капитал концерна D, ей будет легко наверстать упущенное. Единственным законным средством фирмы В в конкурентной борьбе является выбор момента поставки товара на рынок, так как понижение цены на поставляемый товар запрещено определенным соглашением. Для разорения фирмы А фирма В должна минимизировать ее доходы. Пусть технология выпуска товара такова, что чем дольше он находится в производстве, и, следовательно, позже поступает на рынок, тем качество его выше, а реализуется товар только более высокого качества (так как цена на товары разного качества одна и та же). Доход от продажи товара в единицу времени составляет с денежных единиц.
. Цель фирмы В – разорение фирмы А, после чего, используя капитал концерна D, ей будет легко наверстать упущенное. Единственным законным средством фирмы В в конкурентной борьбе является выбор момента поставки товара на рынок, так как понижение цены на поставляемый товар запрещено определенным соглашением. Для разорения фирмы А фирма В должна минимизировать ее доходы. Пусть технология выпуска товара такова, что чем дольше он находится в производстве, и, следовательно, позже поступает на рынок, тем качество его выше, а реализуется товар только более высокого качества (так как цена на товары разного качества одна и та же). Доход от продажи товара в единицу времени составляет с денежных единиц. . Обозначим через
. Обозначим через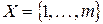 – множество чистых стратегий первого игрока;
– множество чистых стратегий первого игрока;  – множество чистых стратегий второго игрока.
– множество чистых стратегий второго игрока. – вероятность выбора i -й чистой стратегий первым игроком, где
– вероятность выбора i -й чистой стратегий первым игроком, где  ,
,  . Векторы
. Векторы  и
и  называются векторами смешанных стратегий первого и второго игроков соответственно, а множества
называются векторами смешанных стратегий первого и второго игроков соответственно, а множества  и
и  – смешанными расширениями чистых стратегий.
– смешанными расширениями чистых стратегий. ,
,  , то каждая ситуация в чистых стратегиях реализуется с вероятностью
, то каждая ситуация в чистых стратегиях реализуется с вероятностью  . Следовательно, математическое ожидание выигрыша игрока 1 вычисляется по формуле:
. Следовательно, математическое ожидание выигрыша игрока 1 вычисляется по формуле: . (1)
. (1) , где
, где  ,
,  – смешанные расширения чистых стратегий, а функция выигрыша первого игрока (проигрыша второго) вычисляется по формуле (1), называется смешанным расширением матричной игры.
– смешанные расширения чистых стратегий, а функция выигрыша первого игрока (проигрыша второго) вычисляется по формуле (1), называется смешанным расширением матричной игры. называется такая пара смешанных стратегий
называется такая пара смешанных стратегий  ,
,  ,
,  ,
,  – матричные игры, причем
– матричные игры, причем  , где
, где  ,
,  (
( ,
,  .
. – математическое ожидание выигрыша первого игрока в игре
– математическое ожидание выигрыша первого игрока в игре  ,
,  для P1 и Р2 соответственно является выполнение следующих неравенств:
для P1 и Р2 соответственно является выполнение следующих неравенств: .
. – математическое ожидание выигрыша первого игрока в игре
– математическое ожидание выигрыша первого игрока в игре  , v – действительное число,
, v – действительное число,  ,
,  . Необходимым и достаточным условием того, что v – цена игры, а
. Необходимым и достаточным условием того, что v – цена игры, а  ,
,  .
. – математическое ожидание выигрыша первого игрока (проигрыша второго) при условии, что Р1 выбрал свою i -ю чистую стратегию, а Р2 смешанную
– математическое ожидание выигрыша первого игрока (проигрыша второго) при условии, что Р1 выбрал свою i -ю чистую стратегию, а Р2 смешанную  – математическое ожидание выигрыша первого игрока (проигрыша второго) при условии, что Р1 выбрал свою смешанную стратегию
– математическое ожидание выигрыша первого игрока (проигрыша второго) при условии, что Р1 выбрал свою смешанную стратегию  , а Р2 чистую стратегию j.
, а Р2 чистую стратегию j. с ценой
с ценой  справедливы соотношения:
справедливы соотношения: .
. .
. – математическое ожидание выигрыша первого игрока в игре
– математическое ожидание выигрыша первого игрока в игре  , имеем
, имеем  , а для любого j, при котором
, а для любого j, при котором  , имеем
, имеем  .
.
 . Поэтому, в частности, для чистых стратегий i и j имеем:
. Поэтому, в частности, для чистых стратегий i и j имеем: .
. . (*)
. (*)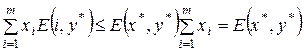 ,
, . (**)
. (**) ;
; .
. – смешанная стратегия первого игрока,
– смешанная стратегия первого игрока,  – смешанная стратегия второго игрока. Тогда, согласно свойствам 2 оптимальных стратегий, выполняются следующие уравнения и неравенства:
– смешанная стратегия второго игрока. Тогда, согласно свойствам 2 оптимальных стратегий, выполняются следующие уравнения и неравенства: ,
,  ,
, (2)
(2)  (2д)
(2д) .
. .
. – смешанная стратегия первого игрока,
– смешанная стратегия первого игрока,  – смешанная стратегия второго игрока. Выпишем для игры соотношения (2) и (2д):
– смешанная стратегия второго игрока. Выпишем для игры соотношения (2) и (2д):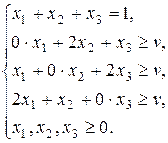

 , то есть оптимальная стратегия Р1 –
, то есть оптимальная стратегия Р1 –  , а оптимальная стратегия Р2 –
, а оптимальная стратегия Р2 –  , оптимальное значение цены игры:
, оптимальное значение цены игры:  .
. .
. .
. , а игрок 2 чистую стратегию j. Тогда математическое ожидание выигрыша первого игрока равно:
, а игрок 2 чистую стратегию j. Тогда математическое ожидание выигрыша первого игрока равно: . (3)
. (3) . Таким образом, каждой чистой стратегии j соответствует своя прямая. Графиком функции
. Таким образом, каждой чистой стратегии j соответствует своя прямая. Графиком функции
 , в которой достигается максимум функции
, в которой достигается максимум функции  для
для  , и дает требуемое оптимальное решение
, и дает требуемое оптимальное решение  , а значение игры
, а значение игры  .
. .
. имеем:
имеем: 


 и сами прямые
и сами прямые  ,
,  функции
функции 


