
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Игры с частными случаями платежных матрицСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Диагональная игра Примером диагональной игры может служить игра в «прятки», состоящая в следующем. 2-й игрок прячется в одну из n ячеек, а 1-й игрок обследует одну из них. Если он выбрал ячейку i и 2-й игрок находится там, то 1-й игрок обнаруживает 2-го игрока с вероятностью
Стратегии оптимальные игроков здесь совпадают; они состоят в выборе ячеек с вероятностями, равными
Симметричная игра
Определение. Квадратрная матрица
Теорема. Знгачение симметричной игры равно нулю. Кроме того, если
Доказательство. Пусть
Поэтому
так что значение игры неположительно. В тоже время
так что значение игры неотрицательно. Следовательно, значение игры равно нулю. Далее, если
Но отсюда
так что
или
Значит, стратегия Пример. («камень–ножницы–бумага»). Каждый игрок во время своего хода независимо от другого выбирает одну из трех стратегий, называемых «камень», «ножницы» и «бумага». Выбранные стратегии сравниваются. Если они совпадают, выигрыш первого игрока составляет 0 (ничья), в противном случае побеждает игрок с более сильной стратегией. «Камень» считается сильнее «ножниц», которые, в свою очередь, сильнее «бумаги», которая сильнее «камня». Выигрыш победившего игрока составляет 1, проигравшего -1. Платежная матрица в этом случае имеет следующий вид:
Так как матрица кососимметрическая, значение игры должно быть равно нулю. Очевидно, эта игра не имеет седловой точки. Кроме того, оптимальная стратегия не может использовать только две чистые стратегии. Действительно, если, например,
Решение этих уравнений § 4. Игры в условиях неопределенности и риска (игры с природой)
В данном параграфе рассмотрим игру, в которой два участника, одним из них (Р2) считается «природа», внешняя среда, ее поведение непредсказуемо. В таких играх сознательно действует только один из игроков (Р1). Природа сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально, хотя могут встретиться ситуации, в которых «игроком» 2 действительно может быть природа (например, обстоятельства, связанные с погодными условиями или с природными стихийными силами). Игра с природой задается одним из следующих способов. 1. Задание матрицей игры.
Данный способ задания аналогичен матричной игре. Пусть первый игрок имеет m возможных стратегий:
2. Задание в виде матрицы рисков Риском Понятие доминирования в играх с природой имеет определенную специфику. Исключать из рассмотрения можно доминируемые стратегии только первого игрока. Методы принятия решений в играх с природой зависят от характера неопределенности: известны или нет вероятности состояний (стратегий) природы, то есть имеет ли место ситуация риска (нет информации о вероятностях) или неопределенности (вероятности известны).
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.150.249 (0.008 с.) |

 в противном случае вероятность обнаружения равна нулю. Целью 1-го игрока является максимизация, а целью 2-го минимизация вероятности обнаружения. Эта игра описывается диагональной матрицей
в противном случае вероятность обнаружения равна нулю. Целью 1-го игрока является максимизация, а целью 2-го минимизация вероятности обнаружения. Эта игра описывается диагональной матрицей .
. ,
, 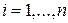
 называется кососимметрической, если
называется кососимметрической, если  для всех
для всех  ,
,  . Матричная игра называется симметричной, если еематрица коссосиметрическая.
. Матричная игра называется симметричной, если еематрица коссосиметрическая. есть оптимальная стратегия для первого игрока, то
есть оптимальная стратегия для первого игрока, то 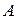 - матрица игры и
- матрица игры и  . Следовательно,
. Следовательно, .
. . Отсюда следует, что для любого
. Отсюда следует, что для любого 
 .
. ,
,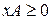 .
. ,
,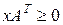
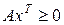 .
. .
.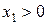 ,
,  и
и  , то легко видеть, что такая смешанная стратегия для первого игрока дает отрицательный ожидаемый выигрыш против первой чистой стратегии второго игрока. Поэтому все компоненты оптимальной стратегии
, то легко видеть, что такая смешанная стратегия для первого игрока дает отрицательный ожидаемый выигрыш против первой чистой стратегии второго игрока. Поэтому все компоненты оптимальной стратегии 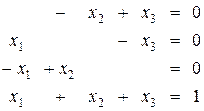 .
.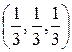 нетрудно найти. Для обоих игрокой это единственная оптимальная стратегия.
нетрудно найти. Для обоих игрокой это единственная оптимальная стратегия. . У природы имеется n возможных состояний:
. У природы имеется n возможных состояний:  . Условия игры с природой задаются матрицей A выигрыша первого игрока:
. Условия игры с природой задаются матрицей A выигрыша первого игрока: , где
, где  – выигрыш первого игрока, который он получит, если выберет стратегию
– выигрыш первого игрока, который он получит, если выберет стратегию  , а состоянием природы будет
, а состоянием природы будет  .
. , или матрицы упущенных возможностей. Величина риска – это размер платы за отсутствие информации о состоянии природы. Матрица
, или матрицы упущенных возможностей. Величина риска – это размер платы за отсутствие информации о состоянии природы. Матрица  может быть построена непосредственно из условий задачи или на основе матрицы выигрышей
может быть построена непосредственно из условий задачи или на основе матрицы выигрышей  игрока при использовании им стратегии
игрока при использовании им стратегии 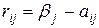 , где
, где  .
.


