
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о статистических играх.(Принятие решений в условиях неопределенности)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ППППринятие решений в условиях неопределённости может быть описано матричными играми особого типа, в которых игрок взаимодействует не со вторым игроком, а с окружающей средой. Объективно окружающая среда не заинтересована в проигрыше игрока. Игрок имеет информацию о том, что окружающая среда может принять одно из нескольких возможных состояний и сталкивается с неопределённостью относительно того конкретного состояния, которое примет среда в данный момент времени. Матричная игра, в которой игрок взаимодействует с окружающей средой, не заинтересованной в его проигрыше, и решает задачу определения наиболее выгодного варианта поведения с учётом неопределённости состояния окружающей среды, называется статистической игрой или «игрой с природой». Игрок в этой игре называется лицом, принимающим решение (ЛПР). [3,6,9,10]. В общем виде платёжная матрица статистической игры приведена на рисунке 3.1.
Рис. 1. Общий вид платёжной матрицы статистической игры
В данной игре строки матрицы (Ai) - стратегии ЛПР, а столбцы матрицы (Sj) – состояния окружающей среды.
Критерии принятия решения
ЛПР определяет наиболее выгодную стратегию в зависимости от целевой установки, которую он реализует в процессе решения задачи. Результат решения задачи ЛПР определяет по одному из критериев принятия решения. Для того, чтобы прийти к однозначному и по возможности наиболее выгодному решению, необходимо ввести оценочную (целевую) функцию. При этом каждой стратегии ЛПР (Ai) приписывается некоторый результат Wi, характеризующий все последствия этого решения. Из массива результатов принятия решений ЛПР выбирает элемент W, который наилучшим образом отражает мотивацию его поведения.
Критерий максимального математического ожидания выигрыша
Критерий максимального математического ожидания выигрыша применяется в тех случаях, когда ЛПР известны вероятности состояний окружающей среды:
Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой значение математического ожидания (среднего) выигрыша при выборе соответствующей стратегии ЛПР:
Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение математического ожидания выигрыша максимально: W = max Wi Применение критерия максимального математического ожидания выигрыша, таким образом, оправдано, если ситуация, в которой принимается решение, следующая: 1. ЛПР известны вероятности всех состояний окружающей среды; 2. Минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша. Необходимость иметь информацию о вероятностях состояний окружающей среды ограничивает область применения данного критерия.
Критерий недостаточного основания Лапласа Данный критерий используется при наличии неполной информации о вероятностях состояний окружающей среды в задаче принятия решения. Вероятности состояний окружающей среды принимаются равными
Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение среднего выигрыша максимально: W = max Wi Использование данного критерия оправдано в следующей ситуации: 1. ЛПР не имеет информации, либо имеет неполную информацию о вероятностях состояний окружающей среды; 2. Вероятности состояний окружающей среды близки по своим значениям; 3. Минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.
Максиминный критерий Вальда
Правило выбора решения в соответствии с максиминным критерием (ММ-критерием) можно интерпретировать следующим образом: Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой минимальное значение выигрыша в соответствующей стратегии ЛПР:
Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой минимальное значение выигрыша максимально:
Выбранная таким образом стратегия полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство позволяет считать ММ-критерий одним из фундаментальных. Применение ММ-критерия оправдано, если ситуация, в которой принимается решение следующая: 1. О возможности появления состояний окружающей среды ничего не известно; 2. Решение реализуется только один раз; 3. Необходимо исключить какой бы то ни было риск.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.248.140 (0.008 с.) |

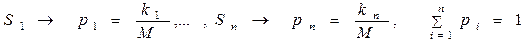
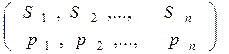
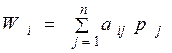 (2)
(2)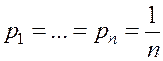 , и по каждой стратегии ЛПР в платёжной матрице определяется среднее значение выигрыша:
, и по каждой стратегии ЛПР в платёжной матрице определяется среднее значение выигрыша: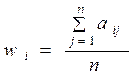 (3)
(3)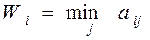 (4)
(4)



