
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Игровые методы принятия решенийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Игровые методы принятия решений Теория игр служит для принятия решений в условиях конфликтов
Рис. 1 Игрой называется идеализированная математическая модель конфликтной ситуации. Стороны, участвующие в конфликте называются игроками, а исход конфликта – выигрышем. Регулярное действие, выполняемое игроком, называется ходом. Совокупность ходов игрока, совершаемых им для достижения цели игры, называется стратегией. Все возможные действия игроков подчиняются определённым правилам. Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д. В зависимости от количества игроков различают игры двух и По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий, игра называется бесконечной. По характеру взаимодействия игры делятся на коалиционные и бескоалиционные. Бескоалиционные – игроки не имеют права вступать в соглашения, образовывать коалиции; коалиционные (кооперативные) – могут вступать в коалиции. В кооперативных играх коалиции заранее определены. По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой. По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые и др. Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 1, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям). Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.) Решение матричных игр в чистых стратегиях. Пусть первый игрок имеет m стратегий, второй n стратегий. Обозначим через В общем виде матричная игра может быть записана следующей матрицей, которая называется платёжной или матрицей выигрышей: Каждая стратегия В каждой партии делается ход: игрок 1 выбирает стратегию i, игрок 2– стратегию j. После чего игрок 1 получает выигрыш Для того чтобы найти решение игры, следует для каждого игрока найти стратегию, которая называется оптимальной. Для первого это стратегия, которая приносит максимальный выигрыш, если второй придерживается своей. В то же время для второго – это стратегия, которая приносит минимальный проигрыш, если первый придерживается своей. Каждый из игроков стремится максимизировать свой выигрыш с учётом поведения противодействующего ему игрока. Возможные действия игроков называются чистыми стратегиями. Что думает игрок 1?
Игрок 1 использует логику, которая гарантирует ему максимальный выигрыш вне зависимости от поведения игрока 2. Значение, равное 4, называется нижней ценой игры. В теории игр предполагается, что оба игрока действуют разумно, т.е. стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим (для себя) образом. Пусть игрок 1 выбрал стратегию i. Тогда в худшем случае он выиграет (при любых стратегий игрока 2)
Затем отыскивается такая стратегия
Стратегия Величина
Что думает игрок 2?
Игрок 2 использует логику, которая гарантирует ему минимальный проигрыш вне зависимости от поведения игрока 1. Свой выбор, игрок 2 остановит на стратегии В1, которая обеспечит ему проигрыш 4, т.е. потерю не более 4 ден.ед. Значение равное 4, называется верхней ценой игры. Стратегия игрока 2 максимально уменьшить выигрыш игрока 1 (за счёт своих стратегий). Поэтому для игрока 2 необходимо определить значение:
для этого надо найти максимальные значения по каждому из столбцов платёжной матрицы, а затем определить минимальное из этих значений. Величина Таким образом, игрок 1 может обеспечить себе выигрыш не менее Если Пример 1. Найти решение игры, заданной платёжной матрицей A в чистых стратегиях Решение: Найдём минимальные элементы в каждой строке и максимальные элементы в каждом столбце. Затем найдём максимальный элемент среди минимальных и минимальный среди максимальных. Занесём всё в следующую таблицу
В нашей задаче Пример 2. Показать, что данная платёжная матрица не имеет решения в чистых стратегиях
Решение: Также как и в предыдущей задаче составим таблицу
Решения в чистых стратегиях не существует, так как нижняя цена игры достигается в стратегии A 2 и её значение равно 30, в то время как верхняя цена игры достигается в стратегии B 2 и её значение равно 40. Биматричные игры. Основные понятия и ситуация равновесия
В матричной игре интересы двух игроков прямо противоположны, т.е. игра антагонистическая. Однако часто встречаются ситуации, когда, в которых интересы игроков хотя и не совпадают, но не обязательно являются противоположными. Рассмотрим конфликтную ситуацию, в которой два игрока имеют следующие возможности для выбора своей линии поведения: - игрок 1 может выбрать любую из стратегий - игрок 2 - любую из стратегий При этом в ситуации
В этом случае говорят о биматричной бескоалиционной игре двух игроков с платежными матрицами (1). При Доминирующие стратегии – стратегии, являющиеся оптимальными вне зависимости, что делает оппонент. Стратегия Рациональные игроки не выбирают строго доминируемых стратегий, их последовательно исключают из рассмотрения. В результате удаляются явно не рациональные стратегии. Свойство 1. Если в бескоалиционной игре (1) последовательно удалить все строго доминируемые стратегии, то множество оставшихся стратегий не зависит от последовательности удаления. Пример. Фирмы 1 и 2 продают конкурирующие товары и решают проводить ли им рекламные компании. Возможные исходы отражены платежными матрицами
Фирма B Фирма B Реклама Нет Реклама Нет
Матрица выигрышей фирмы А Матрица выигрышей фирмы B
Фирма B: доминирующая стратегия – В1 Фирма А: доминирующая стратегия – А1 Критерии принятия решения
ЛПР определяет наиболее выгодную стратегию в зависимости от целевой установки, которую он реализует в процессе решения задачи. Результат решения задачи ЛПР определяет по одному из критериев принятия решения. Для того, чтобы прийти к однозначному и по возможности наиболее выгодному решению, необходимо ввести оценочную (целевую) функцию. При этом каждой стратегии ЛПР (Ai) приписывается некоторый результат Wi, характеризующий все последствия этого решения. Из массива результатов принятия решений ЛПР выбирает элемент W, который наилучшим образом отражает мотивацию его поведения.
Максиминный критерий Вальда
Правило выбора решения в соответствии с максиминным критерием (ММ-критерием) можно интерпретировать следующим образом: Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой минимальное значение выигрыша в соответствующей стратегии ЛПР:
Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой минимальное значение выигрыша максимально:
Выбранная таким образом стратегия полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство позволяет считать ММ-критерий одним из фундаментальных. Применение ММ-критерия оправдано, если ситуация, в которой принимается решение следующая: 1. О возможности появления состояний окружающей среды ничего не известно; 2. Решение реализуется только один раз; 3. Необходимо исключить какой бы то ни было риск.
Игровые методы принятия решений Теория игр служит для принятия решений в условиях конфликтов
Рис. 1 Игрой называется идеализированная математическая модель конфликтной ситуации. Стороны, участвующие в конфликте называются игроками, а исход конфликта – выигрышем. Регулярное действие, выполняемое игроком, называется ходом. Совокупность ходов игрока, совершаемых им для достижения цели игры, называется стратегией. Все возможные действия игроков подчиняются определённым правилам. Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д. В зависимости от количества игроков различают игры двух и По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий, игра называется бесконечной. По характеру взаимодействия игры делятся на коалиционные и бескоалиционные. Бескоалиционные – игроки не имеют права вступать в соглашения, образовывать коалиции; коалиционные (кооперативные) – могут вступать в коалиции. В кооперативных играх коалиции заранее определены. По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой. По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые и др. Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 1, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям). Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 953; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.95 (0.008 с.) |

 игроков. Наиболее изучены игры с двумя игроками. Такие игры называются парными.
игроков. Наиболее изучены игры с двумя игроками. Такие игры называются парными. , i - стратегию игрока 1, через
, i - стратегию игрока 1, через 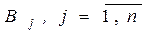 , j - стратегию игрока 2. Паре стратегий
, j - стратегию игрока 2. Паре стратегий  поставим в соответствие число
поставим в соответствие число  - выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою стратегию i, а второй – j.
- выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою стратегию i, а второй – j.
 , называется чистой стратегией.
, называется чистой стратегией. (за счёт игрока 2). Если
(за счёт игрока 2). Если  , значит, игрок 1 платит игроку 2 сумму
, значит, игрок 1 платит игроку 2 сумму  и игра заканчивается.
и игра заканчивается.
 , которая гарантирует ему выигрыш
, которая гарантирует ему выигрыш .
. называется максиминной (осторожной) стратегией игрока 1
называется максиминной (осторожной) стратегией игрока 1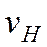 называется максимином матрицы или нижней ценой игры. Нижняя цена игры показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. Принцип выбора оптимальной стратегии, основанной на максимизации минимального выигрыша, называется принципом максимина, или принципом наилучшего гарантированного результата.
называется максимином матрицы или нижней ценой игры. Нижняя цена игры показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. Принцип выбора оптимальной стратегии, основанной на максимизации минимального выигрыша, называется принципом максимина, или принципом наилучшего гарантированного результата.
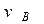 называется минимаксом матрицы или верхней ценой игры. Стратегия
называется минимаксом матрицы или верхней ценой игры. Стратегия  называется минимаксной (осторожной) стратегией игрока 2, если
называется минимаксной (осторожной) стратегией игрока 2, если 
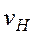 , а игрок 2 может не допустить выигрыш игрока 1 больше чем на
, а игрок 2 может не допустить выигрыш игрока 1 больше чем на  .
. = v, то говорят, что игра имеет решение в чистых стратегиях, а стратегии
= v, то говорят, что игра имеет решение в чистых стратегиях, а стратегии 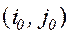 , при которых достигается цена игры = v – оптимальными чистыми стратегиями. Пара чистых стратегий
, при которых достигается цена игры = v – оптимальными чистыми стратегиями. Пара чистых стратегий  называется седловой точкой. Седловой элемент
называется седловой точкой. Седловой элемент  является минимальным в i- строке и максимальным в j - столбце платёжной матрицы. Значение v называется чистой ценой игры.
является минимальным в i- строке и максимальным в j - столбце платёжной матрицы. Значение v называется чистой ценой игры.


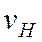 =
=  = v. Пара
= v. Пара 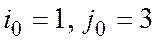 образует седловую точку. Таким образом, оптимальной стратегией для игрока 1 будет стратегия A 1, а для игрока 2 – стратегия В 3. Цена игры v= 4.
образует седловую точку. Таким образом, оптимальной стратегией для игрока 1 будет стратегия A 1, а для игрока 2 – стратегия В 3. Цена игры v= 4.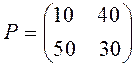

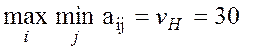
 ;
; .
. выигрыш первого игрока будет
выигрыш первого игрока будет  , а второго -
, а второго - 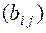 , т.е. игра задается в форме двух платежных матриц
, т.е. игра задается в форме двух платежных матриц  :
: . (1)
. (1) получаем обычную матричную игру.
получаем обычную матричную игру. называется строго доминируемой стратегией
называется строго доминируемой стратегией  , а стратегия
, а стратегия  – доминирующей, если при любом варианте поведения противодействующего игрока выполняются неравенства
– доминирующей, если при любом варианте поведения противодействующего игрока выполняются неравенства  .
.

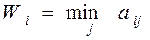 (4)
(4)



