
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение матричных игр со смешанным расширением методами линейного программированияСодержание книги
Поиск на нашем сайте
Решение матричной игры со смешанным расширением – это определение оптимальных смешанных стратегий, то есть нахождение таких значений вероятностей выбора чистых стратегий для обоих игроков, при которых они достигают наибольшего выигрыша. Для матричной игры, платёжная матрица которой показана на рис. 1,
Рис. 1
Если один из игроков придерживается своей оптимальной стратегии, то, по условию задачи, его выигрыш не может быть меньше цены игры v. Поэтому данная задача может быть представлена для игроков в виде следующих систем линейных неравенств:
Для первого игрока:
Для второго игрока
Чтобы определить значение v, разделим обе части каждого из уравнений на v. Введем обозначения
Из первой системы найдем отношение 1/ v, в котором величина v должна равняться максимальной цене игры для игрока 1. Сформируем целевую функцию для первого игрока
Для игрока 2 необходимо найти минимальную цену игры (v), следовательно величина 1/ v должна стремиться к максимуму, т.е.
Все переменные в данных системах линейных неравенств должны быть неотрицательными, а также цена игры v не была бы отрицательной. Цена игры вычисляется на основе коэффициентов выигрышей платёжной матрицы. Поэтому, для гарантии неотрицательности всех переменных, необходимо, чтобы все коэффициенты матрицы были неотрицательными. Этого можно добиться, прибавив перед началом решения задачи к каждому коэффициенту матрицы число Для решения задач линейного программирования используется симплекс-метод. [1, 5]. В результате решения определяются значения целевых функций (для обоих игроков эти значения совпадают), а также значения переменных xi и yj. Величина v * определяется по формуле: v * = 1/ z Значения вероятностей выбора стратегий определяются: для игрока 1: Для определения цены игры v из величины v * необходимо вычесть число K.
Биматричные игры. Основные понятия и ситуация равновесия
В матричной игре интересы двух игроков прямо противоположны, т.е. игра антагонистическая. Однако часто встречаются ситуации, когда, в которых интересы игроков хотя и не совпадают, но не обязательно являются противоположными. Рассмотрим конфликтную ситуацию, в которой два игрока имеют следующие возможности для выбора своей линии поведения: - игрок 1 может выбрать любую из стратегий - игрок 2 - любую из стратегий При этом в ситуации
В этом случае говорят о биматричной бескоалиционной игре двух игроков с платежными матрицами (1). При Доминирующие стратегии – стратегии, являющиеся оптимальными вне зависимости, что делает оппонент. Стратегия Рациональные игроки не выбирают строго доминируемых стратегий, их последовательно исключают из рассмотрения. В результате удаляются явно не рациональные стратегии. Свойство 1. Если в бескоалиционной игре (1) последовательно удалить все строго доминируемые стратегии, то множество оставшихся стратегий не зависит от последовательности удаления. Пример. Фирмы 1 и 2 продают конкурирующие товары и решают проводить ли им рекламные компании. Возможные исходы отражены платежными матрицами
Фирма B Фирма B Реклама Нет Реклама Нет
Матрица выигрышей фирмы А Матрица выигрышей фирмы B
Фирма B: доминирующая стратегия – В1 Фирма А: доминирующая стратегия – А1
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.210 (0.008 с.) |

 . Определим такие значения вероятностей выбора стратегий для игрока 1
. Определим такие значения вероятностей выбора стратегий для игрока 1  и для игрока 2
и для игрока 2  , при которых игроки достигали бы своего максимально гарантированного выигрыша.
, при которых игроки достигали бы своего максимально гарантированного выигрыша.

 и запишем системы неравенств в следующей форме
и запишем системы неравенств в следующей форме

 .
.
 , соответствующее модулю наименьшего отрицательного коэффициента матрицы. Тогда в ходе решения задачи будет определена не цена игры, а величина
, соответствующее модулю наименьшего отрицательного коэффициента матрицы. Тогда в ходе решения задачи будет определена не цена игры, а величина  .
. : для игрока 2:
: для игрока 2:  .
. ;
; .
. выигрыш первого игрока будет
выигрыш первого игрока будет  , а второго -
, а второго - 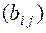 , т.е. игра задается в форме двух платежных матриц
, т.е. игра задается в форме двух платежных матриц  :
: . (1)
. (1) получаем обычную матричную игру.
получаем обычную матричную игру. называется строго доминируемой стратегией
называется строго доминируемой стратегией  , а стратегия
, а стратегия  – доминирующей, если при любом варианте поведения противодействующего игрока выполняются неравенства
– доминирующей, если при любом варианте поведения противодействующего игрока выполняются неравенства  .
.




