
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о матричных играх со смешанными стратегиямиСодержание книги Поиск на нашем сайте
Решения матричной игры начинается с нахождения её верхней и нижней цены. Если эти значения совпадают и игра имеет седловую точку, то на этом решение игры завершается. Если же матричная игра не имеет решения в чистых стратегиях, то для нахождения её решения используются так называемые смешанные стратегии, а найденные ранее нижняя и верхняя цены игры указывают на то, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. В этом случае оптимальный результат игры достигается путём применения чистых стратегий случайно, с определённой вероятностью. Рассмотрим, например, игру:
В этой игре Если каждый из игроков применяет отмеченную звездочкой стратегию ( Секретность можно сохранить, если каждый раз выбирать стратегию случайным образом, используя для этого какой-либо механизм случайного выбора.
Для механизма случайного выбора выигрыши и проигрыши игроков будут случайными величинами. Результат игры в этом случае можно оценить средней величиной проигрыша второго игрока. Вернемся к примеру. Так, если второй игрок использует стратегию
а при стратегии первого игрока
Следовательно, второй игрок может ограничить свой средний проигрыш значением 4,5 независимо от стратегии, применяемой первым игроком. Стратегию, основанную на случайном выборе, называют смешанной стратегией. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий. Стратегии, применённые с вероятностью, отличной от нуля, называются активными стратегиями. Пусть игрок 1 имеет m чистых стратегий
Аналогично для игрока 2. Обозначим через
Для соблюдения секретности, каждый игрок применяет свои смешанные стратегии независимо от выбора другого игрока. Доказано, что для всех игр со смешанным расширением существует оптимальная смешанная стратегия, значение выигрыша при выборе которой находится в интервале между нижней и верхней ценой игры: При этом условии величина v называется ценой игры. Если
Определение оптимальных стратегий для обоих игроков и цены игры и составляет процесс нахождения решения игры. Доказано, что всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях. Для того чтобы число v было ценой игры, а
Для игр с нулевой суммой справедливо следующее утверждение: если один из игроков применяет свою оптимальную смешанную стратегию, то его выигрыш равен цене игры v вне зависимости от того, с какими вероятностями будет применять второй игрок стратегии, вошедшие в оптимальные (в том числе и чистые стратегии). И для достижения наибольшего гарантированного выигрыша второму игроку также необходимо придерживаться своей оптимальной смешанной стратегии.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1085; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.119 (0.007 с.) |




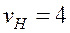 и
и  . Следовательно, первый игрок может гарантировать себе выигрыш, равный 4, а второй может ограничить свой проигрыш 5. Область между
. Следовательно, первый игрок может гарантировать себе выигрыш, равный 4, а второй может ограничить свой проигрыш 5. Область между  и
и  является как бы ничейной и каждый игрок может попытаться улучшить свой результат за счет этой области. Каковы же должны быть в этом случае оптимальные стратегии игроков?
является как бы ничейной и каждый игрок может попытаться улучшить свой результат за счет этой области. Каковы же должны быть в этом случае оптимальные стратегии игроков? и
и  ), то выигрыш первого игрока и проигрыш второго будут равны 5. Это невыгодно второму игроку, так как первый выигрывает больше, чем он может себе гарантировать. Однако если второй игрок каким-либо образом раскроет замысел первого о намерении использовать стратегию
), то выигрыш первого игрока и проигрыш второго будут равны 5. Это невыгодно второму игроку, так как первый выигрывает больше, чем он может себе гарантировать. Однако если второй игрок каким-либо образом раскроет замысел первого о намерении использовать стратегию 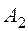 , то он может применить стратегию
, то он может применить стратегию  и уменьшить выигрыш первого до 4. Правда, если первый игрок раскроет замысел второго применить стратегию
и уменьшить выигрыш первого до 4. Правда, если первый игрок раскроет замысел второго применить стратегию  , то, используя стратегию
, то, используя стратегию 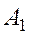 , он увеличит свой выигрыш до 6. Таким образом, возникает ситуация, когда каждый игрок должен хранить в секрете ту стратегию, которую он собирается использовать. Однако, как это сделать? Ведь если партия играется многократно и второй игрок применяет все время стратегию
, он увеличит свой выигрыш до 6. Таким образом, возникает ситуация, когда каждый игрок должен хранить в секрете ту стратегию, которую он собирается использовать. Однако, как это сделать? Ведь если партия играется многократно и второй игрок применяет все время стратегию  , то первый игрок скоро разгадает замысел второго и, применив стратегию
, то первый игрок скоро разгадает замысел второго и, применив стратегию  , будет иметь добавочный выигрыш. Очевидно, что второй игрок должен менять стратегию в каждой новой партии, но делать это он должен так, чтобы первый не догадался, какую стратегию применит он в каждом случае.
, будет иметь добавочный выигрыш. Очевидно, что второй игрок должен менять стратегию в каждой новой партии, но делать это он должен так, чтобы первый не догадался, какую стратегию применит он в каждом случае.

 и
и  случайным образом с вероятностями 0.5; 0.5, то при стратегии первого игрока
случайным образом с вероятностями 0.5; 0.5, то при стратегии первого игрока  среднее значение его проигрыша будет:
среднее значение его проигрыша будет:

 .
. . Обозначим через
. Обозначим через  вероятности, с которыми игрок 1 использует свои соответствующие чистые стратегии. Тогда смешанная стратегия игрока 1 – это набор чисел
вероятности, с которыми игрок 1 использует свои соответствующие чистые стратегии. Тогда смешанная стратегия игрока 1 – это набор чисел 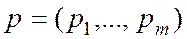 , удовлетворяющих соотношениям
, удовлетворяющих соотношениям
 вероятности, с которыми он использует свои чистые стратегии
вероятности, с которыми он использует свои чистые стратегии  . Смешанная стратегия для игрока 2 – набор чисел
. Смешанная стратегия для игрока 2 – набор чисел  , удовлетворяющих соотношениям
, удовлетворяющих соотношениям
 .
. – оптимальная стратегия первого игрока, а
– оптимальная стратегия первого игрока, а  – оптимальная стратегия второго игрока, то число
– оптимальная стратегия второго игрока, то число является ценой игры.
является ценой игры. и
и 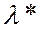 оптимальными стратегиями необходимо и достаточно выполнение неравенств
оптимальными стратегиями необходимо и достаточно выполнение неравенств



