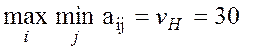Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение матричных игр в чистых стратегиях.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть первый игрок имеет m стратегий, второй n стратегий. Обозначим через В общем виде матричная игра может быть записана следующей матрицей, которая называется платёжной или матрицей выигрышей: Каждая стратегия В каждой партии делается ход: игрок 1 выбирает стратегию i, игрок 2– стратегию j. После чего игрок 1 получает выигрыш Для того чтобы найти решение игры, следует для каждого игрока найти стратегию, которая называется оптимальной. Для первого это стратегия, которая приносит максимальный выигрыш, если второй придерживается своей. В то же время для второго – это стратегия, которая приносит минимальный проигрыш, если первый придерживается своей. Каждый из игроков стремится максимизировать свой выигрыш с учётом поведения противодействующего ему игрока. Возможные действия игроков называются чистыми стратегиями. Что думает игрок 1?
Игрок 1 использует логику, которая гарантирует ему максимальный выигрыш вне зависимости от поведения игрока 2. Значение, равное 4, называется нижней ценой игры. В теории игр предполагается, что оба игрока действуют разумно, т.е. стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим (для себя) образом. Пусть игрок 1 выбрал стратегию i. Тогда в худшем случае он выиграет (при любых стратегий игрока 2)
Затем отыскивается такая стратегия
Стратегия Величина
Что думает игрок 2?
Игрок 2 использует логику, которая гарантирует ему минимальный проигрыш вне зависимости от поведения игрока 1. Свой выбор, игрок 2 остановит на стратегии В1, которая обеспечит ему проигрыш 4, т.е. потерю не более 4 ден.ед. Значение равное 4, называется верхней ценой игры. Стратегия игрока 2 максимально уменьшить выигрыш игрока 1 (за счёт своих стратегий). Поэтому для игрока 2 необходимо определить значение:
для этого надо найти максимальные значения по каждому из столбцов платёжной матрицы, а затем определить минимальное из этих значений. Величина Таким образом, игрок 1 может обеспечить себе выигрыш не менее Если Пример 1. Найти решение игры, заданной платёжной матрицей A в чистых стратегиях Решение: Найдём минимальные элементы в каждой строке и максимальные элементы в каждом столбце. Затем найдём максимальный элемент среди минимальных и минимальный среди максимальных. Занесём всё в следующую таблицу
В нашей задаче Пример 2. Показать, что данная платёжная матрица не имеет решения в чистых стратегиях
Решение: Также как и в предыдущей задаче составим таблицу
Решения в чистых стратегиях не существует, так как нижняя цена игры достигается в стратегии A 2 и её значение равно 30, в то время как верхняя цена игры достигается в стратегии B 2 и её значение равно 40.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.49 (0.007 с.) |

 , i - стратегию игрока 1, через
, i - стратегию игрока 1, через 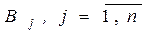 , j - стратегию игрока 2. Паре стратегий
, j - стратегию игрока 2. Паре стратегий  поставим в соответствие число
поставим в соответствие число  - выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою стратегию i, а второй – j.
- выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою стратегию i, а второй – j.
 , называется чистой стратегией.
, называется чистой стратегией. (за счёт игрока 2). Если
(за счёт игрока 2). Если  , значит, игрок 1 платит игроку 2 сумму
, значит, игрок 1 платит игроку 2 сумму  и игра заканчивается.
и игра заканчивается.
 , которая гарантирует ему выигрыш
, которая гарантирует ему выигрыш .
. называется максиминной (осторожной) стратегией игрока 1
называется максиминной (осторожной) стратегией игрока 1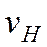 называется максимином матрицы или нижней ценой игры. Нижняя цена игры показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. Принцип выбора оптимальной стратегии, основанной на максимизации минимального выигрыша, называется принципом максимина, или принципом наилучшего гарантированного результата.
называется максимином матрицы или нижней ценой игры. Нижняя цена игры показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. Принцип выбора оптимальной стратегии, основанной на максимизации минимального выигрыша, называется принципом максимина, или принципом наилучшего гарантированного результата.
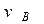 называется минимаксом матрицы или верхней ценой игры. Стратегия
называется минимаксом матрицы или верхней ценой игры. Стратегия  называется минимаксной (осторожной) стратегией игрока 2, если
называется минимаксной (осторожной) стратегией игрока 2, если 
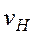 , а игрок 2 может не допустить выигрыш игрока 1 больше чем на
, а игрок 2 может не допустить выигрыш игрока 1 больше чем на  .
. = v, то говорят, что игра имеет решение в чистых стратегиях, а стратегии
= v, то говорят, что игра имеет решение в чистых стратегиях, а стратегии 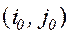 , при которых достигается цена игры = v – оптимальными чистыми стратегиями. Пара чистых стратегий
, при которых достигается цена игры = v – оптимальными чистыми стратегиями. Пара чистых стратегий  называется седловой точкой. Седловой элемент
называется седловой точкой. Седловой элемент  является минимальным в i- строке и максимальным в j - столбце платёжной матрицы. Значение v называется чистой ценой игры.
является минимальным в i- строке и максимальным в j - столбце платёжной матрицы. Значение v называется чистой ценой игры.


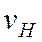 =
=  = v. Пара
= v. Пара 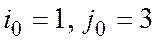 образует седловую точку. Таким образом, оптимальной стратегией для игрока 1 будет стратегия A 1, а для игрока 2 – стратегия В 3. Цена игры v= 4.
образует седловую точку. Таким образом, оптимальной стратегией для игрока 1 будет стратегия A 1, а для игрока 2 – стратегия В 3. Цена игры v= 4.