
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Менеджмент как процесс принятия управленческих решений. Виды управленческих решений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Менеджмент как процесс принятия управленческих решений. Виды управленческих решений. Технология менеджмента рассматривает управленческое решение как процесс, состоящий из трех стадий: подготовка решения: принятие решения; реализация решения.
Факторы, влияющие на процесс принятия решений: личностные, ситуационные. Классификация неопределенных факторов по источнику неопределенности и по природе неопределенности. Личностные факторы определяются своеобразием психических процессов, состояний и качеств ЛПР, влияющих на процесс принятия решений. Поэтому их можно представить в виде трех уровней, соответствующих традиционной психической структуре личности. К ним относятся психические процессы, психические состояния и психические свойства. Ситуационные факторы. Принятие решений зависит не только от психологических особенностей ЛПР, но также от ситуационных факторов, т.е. конкретных обстоятельств, в которых принимается управленческое решение. Эта группа включает в себя факторы внешней и внутренней среды организации, которые влияют на разработку, оценивание, выбор и реализацию альтернатив (экономические условия, социокультурные факторы, природно-географические факторы). По источнику неопределенности различают факторы неопределенности среды и факторы личностной неопределенности: - Неопределенность среды возникает в условиях неполной информации о значениях факторов внешней или внутренней среды организации. По природе неопределенности. По этому основанию выделяют вероятностную неопределенность и неопределенность уверенности. - К вероятностной неопределенности относят влияние случайных факторов, т.е. таких неопределенных факторов, которые при массовом появлении обладают свойством статистической устойчивости и описываются некоторым законом распределения вероятности. - Неопределенность уверенности характеризуется влиянием неслучайных факторов, т.е. таких факторов, которые не обладают свойством статистической устойчивости.
Понятия цели, проблемы, проблемной ситуации, управления по отклонению/возмущению, управляющих воздействий, задачи принятия решений, системы предпочтений, альтернативы и объектов выбора.
Проблема →Цель→Задача→Решение Под проблемой понимается: 1)несоответствие фактического состояния объект управления желаемому заданному запланированному. 2)вопрос который не имеет готового решения на момент его постановки. Решение проблемы означает: 1)найден вариант действий, но еще не осуществлен. 2)устранены некоторые препятствия или трудности. 3)итог деятельности. Проблемная ситуация – это рассмотрение проблемы с учетом воздействия на нее факторов и условий. Описание проблемной ситуации содержит в себе 2части:: 1)характеристика самой проблемы:2)описание причин или факторов приведенных к появлению проблемы. Управляющие воздействия - это действия руководителей, которые направлены на изменение управляемых факторов внешней и внутренней среды организации с целью обеспечения максимальной или требуемой эффективности управляемого процесса. Задача принятия решений (ЗПР) -- одна из самых распространенных в любой предметной области. Ее решение сводится к выбору одной или нескольких лучших альтернатив из некоторого набора. Для того чтобы сделать такой выбор, необходимо четко определить цель и критерии (показатели качества), по которым будет проводиться оценка некоторого набора альтернативных вариантов. Выбор метода решения такой задачи зависит от количества и качества доступной информации. Данные, необходимые для осуществления обоснованного выбора, можно разделить на четыре категории: информация об альтернативных вариантах, информация о критериях выбора, информация о предпочтениях, информация об окружении задач. Общая схема процесса принятия решений включает следующие основные этапы: Этап 1. Предварительный анализ проблемы. На этом этапе определяются: * главные цели; * уровни рассмотрения, элементы и структура системы (процесса), типы связей; * подсистемы, используемые ими основные ресурсы и критерии качества функционирования подсистем; * основные противоречия, узкие места и ограничения. Этап 2. Постановка задачи. Постановка конкретной ЗПР включает: * формулирование задачи; * определение типа задачи; * определение множества альтернативных вариантов и основных критериев для выбора из них наилучших; * выбор метода решения ЗПР.
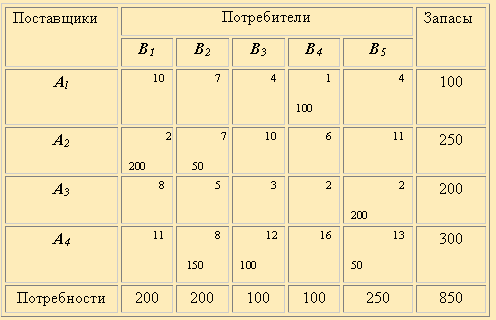
Этап 3. Получение исходных данных Этап 4. Решение ЗПР с привлечением математических методов и вычислительной техники, экспертов и лица, принимающего решение. Этап 5. Анализ и интерпретация полученных результатов. Полученные результаты могут оказаться неудовлетворительными и потребовать изменений в постановке ЗПР. Таблица 2.3
У поставщика А2 осталось 150 ед. груза. Удовлетворяем потребителя B2 за счет оставшегося у поставщика А2 груза. Для этого сравниваем этот остаток с потребностями потребителя B2: 150<200, записываем 150 ед. в клетку А2B2 и, так как запасы А2 полностью израсходованы, прочеркиваем остальные клетки второй строки. Потребности B2 остались неудовлетворенными на 50 ед. Удовлетворяем их за счет поставщика А3 и переходим к удовлетворению B3 за счет остатка, имеющегося у поставщика А3, и т. д. Процесс продолжаем до тех пор, пока не удовлетворим всех потребителей за счет запасов поставщиков. На этом построение первоначального опорного плана заканчивается. Найдем общую стоимость составленного плана как сумму произведений объемов перевозок, стоящих в левом углу занятых клеток, на соответствующие стоимости в этих же ячейках: Z = 100 *10 + 100*2 + 150 *7+ 50 *5 + 100*3 + 50*2 + 50*16+ 250*13 = 6950 (eд. стоимости) 2) Метод наименьшей стоимости. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Составим с помощью этого метода опорный план уже рассмотренной задачи. Запишем ее условие в таблицу (табл. 2.5). Выбираем в таблице наименьшую стоимость (это стоимость, помещенная в клетке A1, B4) так как A1 = b4, 100 ед. груза помещаем в этой клетке и исключаем из рассмотрения первую строку и четвертый столбец. В оставшейся таблице стоимостей наименьшей является стоимость, расположенная в клетке A2 , B1 и в клетке A3 , B5. Заполняем любую из них, например A2 , B1. Имеем 200 < 250, следовательно, записываем в нее 200 и исключаем из рассмотрения столбец B1. В клетку A3 , B5 записываем 200 ед. и исключаем из рассмотрения строку A3 . В оставшейся таблице стоимостей снова выбираем наименьшую стоимость и продолжаем процесс до тех пор, пока все запасы не будут распределены, а потребности удовлетворены. В результате получен план
Таблица 2.5
План не содержит циклов и состоит из семи положительных перевозок, следовательно, является вырожденным опорным планом. Определим его стоимость: 3).Метод аппроксимации Фогеля Данный метод состоит в следующем: на каждой итерации находят разности между двумя наименьшими тарифами во всех строках и столбцах, записывая их в дополнительные столбец и строку таблицы; находят max Δcij и заполняют клетку с минимальной стоимостью в строке (столбце), которой соответствует данная разность. Процесс продолжается до тех пор, пока все грузы не будут развезены по потребителям. Данный метод в ряде задач приводит к оптимальному плану. Решим этим методом задачу из примера 2.6.1 (см. табл.2.7).
На первом шаге заполняем клетку A3 B1 (max Δc = 5 и min cij = 6), исключаем 1-ый столбец, отметив в дополнительной строке буквой «В» факт выполнения заказа пункта B1 . Находим новые разности минимальных тарифов по строкам (в столбцах они не изменились) и max Δc = 2 в 1-ой строке и в 4-ом столбце. Заполняем клетку A1B4 и исключаем 4-й столбец и т.д. В конце остается последовательно заполнить клетки 3-го столбца остатками запасов в A1 , A3 , A2 . Составленный опорный план дает значение Z3 = 909 < Z2. Распределительный метод Один из наиболее простых методов решения транспортных задач - распределительный метод. Пусть для транспортной задачи найдено начальное опорное решение Х1 и вычислено значение целевой функции на этом решении F(Х1). По доказанной выше теореме для каждой свободной клетки таблицы задачи можно построить единственный цикл, который содержит эту клетку и часть клеток, занятых опорным решением. Обозначив этот цикл и осуществив сдвиг (перераспределение груза) по циклу на величину
Определим, как изменится целевая функция при переходе к новому опорному решению. При сдвиге на единицу груза по циклу, соответствующему клетке (l,m), приращение целевой функции Δlm равно разности двух сумм:
где Если разность сумм для свободной клетки (l, m) меньше нуля, т.е. Δ lm< 0, то перераспределение величины θ по соответствующему циклу приведет к уменьшению значения F(X) на величину θ • Δlm, т.е. опорное решение можно улучшить. Если же величины Δlm, называемые оценками, для всех свободных клеток таблицы транспортной задачи неотрицательны, то значение целевой функции нельзя уменьшить и опорное решение оптимально. Следовательно, признаком оптимальности распределительного метода является условие
Для каждого нового опорного решения вычисление оценок начинается с первой свободной клетки таблицы. Очередность проверяемых свободных клеток целесообразно устанавливать в порядке возрастания стоимости перевозок cij,так как решается задача на нахождение минимума. ПРИМЕР. Решить распределительным методом транспортную задачу, исходные данные которой приведены в таблице:
Таблица 3.6.1
В левой колонке записаны номера кандидатов, в верхней строке – номера работ. В В венгерском методе используется следующий принцип: оптимальность решения задачи о назначениях не нарушается при уменьшении (увеличении) элементов строки (столбца) на одну и ту же величину. Решение считается оптимальным, если все измененные таким образом затраты
Алгоритм метода содержит следующие шаги. Шаг 1. Получение нулей в каждой сроке. Для этого в каждой строке определяют наименьший элемент, и его значение отнимают от всех элементов этой строки. Переход к шагу 2. Шаг 2. Получение нулей в каждом столбце. В преобразованной таблице в каждом столбце определяют минимальный элемент, и его значение вычитают из всех элементов этого столбца. Переход к шагу 3. Шаг 3. Поиск оптимального решения. Просматривают строку, содержащую наименьшее число нулей. Отмечают один из нулей этой строки и зачеркивают все остальные нули этой строки и того столбца, в котором находится отмеченный нуль. Аналогичные операции последовательно проводят для всех строк. Если назначение, которое получено при всех отмеченных нулях, является полным (т.е. число отмеченных нулей равно Шаг 4. Поиск минимального набора строк и столбцов, содержащих все нули. Для этого необходимо отметить: 1) все строки, в которых не имеется ни одного отмеченного нуля; 2) все столбцы, содержащие перечеркнутый нуль хотя бы в одной из отмеченных строк; 3) все строки, содержащие отмеченные нули хотя бы в одном из отмеченных столбцов. Действия 2) и 3) повторяются поочередно до тех пор, пока есть что отмечать. После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец. Цель этого шага – провести минимальное число горизонтальных и вертикальных прямых, пересекающих по крайней мере один раз все нули. Шаг 5. Перестановка некоторых нулей. Взять наименьшее число из тех клеток, через которые проведены прямые. Вычесть его из каждого числа, стоящего в невычеркнутых столбцах и прибавить к каждому числу, стоящему в вычеркнутых строках. Эта операция не изменяет оптимального решения, после чего весь цикл расчета повторить, начиная с шага 3. Задача о рюкзаке. Задача о загрузке (задача о рюкзаке) и различные её модификации широко применяются на практике в прикладной математике, криптографии, экономике, логистике, для нахождения решения оптимальной загрузки различных транспортных средств: самолетов, кораблей, железнодорожных вагонов и т.д. Задача о ранце – одна из задач комбинаторной оптимизации. Классическая задача о ранце известна очень давно. Вот её постановка: Имеется набор из N предметов, каждый предмет имеет массу Wi и полезность Vi, i=(1,2..N), требуется собрать набор с максимальной полезностью таким образом, чтобы он имел вес не больше W, где W – вместимость ранца. Пример: Задание. В рюкзак объема V = 7 кладут N = 5 предметов.Объемы, веса и количество предметов в каждой группе приведены в таблице.
Максимизировать общий вес рюкзака. Решение. I этап. Условная оптимизация. Таблица 1 – Расчет значения функции f1(L)
f2(L) = max[3x2 + f1(L - 2x2)]; 0 < x2 < 3; x2 = 0,1,2,3.
f3(L) = max[2x3 + f2(L - 3x3)]; 0 < x3 < 3; x3 = 0,1,2,3.
II этап. Безусловная оптимизация.
Рассмотрим задачу оптимального линейного раскроя. Есть достаточно большое число одномерных заготовок одинаковой длины D = 2,6 м. Заготовки следует разрезать на детали 3 типов длиной L = (1,5; 0,9; 1,2). По данным числам D и Li составить матрицу всех возможных способов раскроя A = aij, где каждое aij указывает количество деталей i типа, что выходит из одной заготовки при раскрое по j способому, если заданы также потребности B = (45, 74, 66), в деталях i типа. Решение Составим таблицу исходных данных:
Получим задачу целочисленного линейного программирования: z = x 1 + x 2 + x 3 + x 4 → min
1) Первый этап Найдем решение, отбросив условие целочисленности. Изменим знаки целевой функции на противоположные и будем рассматривать задачу на максимум: Сведем задачу к каноническому виду, для чего прибавим дополнительные или базисные векторы [АКУ, с. 12]:
Для увеличения количества базисных векторов отнимаем от строки, которая содержит отрицательную вспомогательную переменную и максимальный B 2 = 74 все строки с отрицательными вспомогательными переменными (1, 3) [ГЕТ, с. 177]. z = - x 1 - x 2 - x 3 - x 4 – Mz 1 → max, где M - большое число. Построим начальную симплекс-таблицу, где
Δ2 = -2 M + 1. Строка 3 есть ключевой, поскольку в ней минимальное Q 3 = 4.
Строка 1 есть ключевой, поскольку в ней минимальное Q 1 = 21/2.
Решение имеет дробные значения, поэтому переходим ко 2 этапу. 2) Второй этап Применим метод Гомори для поиска целочисленного решения [АКУ, с. 180].
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.181.250 (0.016 с.) |




 можно получить новое опорное решение Х2.
можно получить новое опорное решение Х2.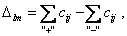
 - сумма стоимостей перевозок единиц груза в нечетных клетках цикла, отмеченных знаком “+”;
- сумма стоимостей перевозок единиц груза в нечетных клетках цикла, отмеченных знаком “+”; 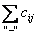 - сумма стоимостей перевозок единиц груза в четных клетках цикла, отмеченных знаком “-”.
- сумма стоимостей перевозок единиц груза в четных клетках цикла, отмеченных знаком “-”. 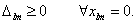
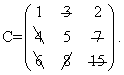
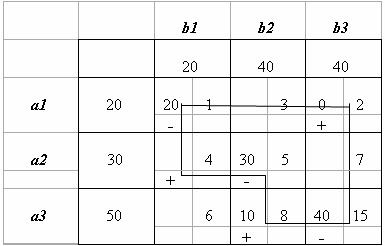
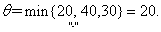 Приращение целевой функции ΔF=-7∙20=-140. Получим новое опорное решение X2. Значение целевой функции на нем F(X2)=20∙2+20∙4+10∙5+30∙8+20∙15=710.
Приращение целевой функции ΔF=-7∙20=-140. Получим новое опорное решение X2. Значение целевой функции на нем F(X2)=20∙2+20∙4+10∙5+30∙8+20∙15=710. 
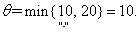 . Приращение целевой функции ΔF=-5∙10=-50. Получаем третье опорное решение X3. Значение целевой функции на нем F(X3)=20∙2+20∙4+10∙7+40∙8+10∙15=660.
. Приращение целевой функции ΔF=-5∙10=-50. Получаем третье опорное решение X3. Значение целевой функции на нем F(X3)=20∙2+20∙4+10∙7+40∙8+10∙15=660. 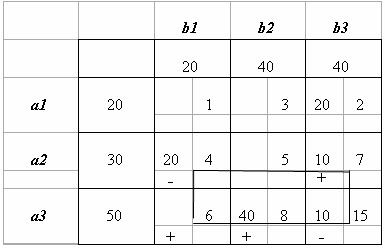
 Приращение целевой функции ΔFm=-6∙10=-60. Получаем четвертое опорное решение X4 Значение целевой функции на нем F(X4)=20 ∙2+10∙4+20∙7+10∙6+40∙8=600.
Приращение целевой функции ΔFm=-6∙10=-60. Получаем четвертое опорное решение X4 Значение целевой функции на нем F(X4)=20 ∙2+10∙4+20∙7+10∙6+40∙8=600. 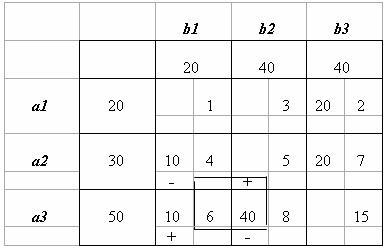
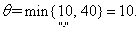 Приращение целевой функции ΔF=-1∙10=-10. Получаем пятое опорное решение X5.
Приращение целевой функции ΔF=-1∙10=-10. Получаем пятое опорное решение X5. 
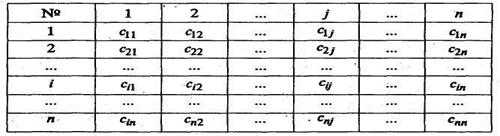
 -й строке
-й строке  -мстолбце стоят затраты на выполнение
-мстолбце стоят затраты на выполнение  , (
, ( ;
;  ) и можно отыскать такой набор
) и можно отыскать такой набор  , что
, что
 ), то решение является оптимальным, в противном случае следует переходить к шагу 4.
), то решение является оптимальным, в противном случае следует переходить к шагу 4.





 на основании строки,
на основании строки, 






