Сетевые и потоковые модели. Понятие пути, продолжительности пути, критического пути, раннего и позднего срока выполнения работ, полного и свободного резерва. Коэффициент напряженности работ.

Одно из важнейших понятий сетевого графика – понятие пути. Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим. Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути. По существу, критический путь – "узкое" место проекта. Уменьшить общую продолжительность осуществления проекта можно, только изыскав способы сокращения работ, лежащих на критическом пути.

Ранний срок (ожидаемый момент) осуществления j-го события представляет собой момент времени, раньше которого событие произойти не может и рассчитывается по формуле

Поздний срок (предельный момент) осуществления i-го собы­тия показывает максимальную задержку во времени наступления данного события:

 

.

Критический путь – последовательность работ между начальными и конечными событиями сети, имеющих наибольшую продолжительность во времени. Минимальное время, необходимое для выполнения проекта, запланированного сетевым графиком, равно длине критического пути. Сетевой график может содержать не один, а несколько критических путей. Критическими называются также работы и события, расположенные на этом пути.Резервный интервал от t до t* для событий, лежащих на критическом пути, равен 0. Для завершающего события сетевого графика поздний срок свершения события должен равняться его раннему сроку, т. е. t_п = t*_п.

Длина критического пути равна раннему сроку свершения завершающего события, т. е. t_кр = t_п = t*_п.

Резервы времени работ

Любая из работ пути L на его участке, не совпадающем с критическим путем (замкнутым между двумя событиями критического пути), обладает резервом времени.

Среди резервов времени работ наиболее часто используют полный и свободный резервы времени работ.

Полный резерв времени работы P_i,j показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв определяется по формуле

 

.

Свободный резерв времени работы P_i,j представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. находится по формуле

 

.

Работы, лежащие на критическом пути, так же, как и критические события, резервов времени не имеют.

Полный резерв времени работы равен резерву максимального из путей, проходящего через данную работу. Этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершится в самый ранний срок, и можно допустить свершение конечного события в его самый поздний срок.

Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем полным путям, проходящим через нее. При использовании полного резерва времени только для одной работы резервы времени остальных работ, лежащих на максимальном пути, проходящим через нее, будут полностью исчерпаны. Резервы времени работ, лежащих на других (немаксимальных по длительности) путях, проходящих через эту работу, сократятся соответственно на величину использованного резерва.
Свободным резервом времени можно пользоваться для предотвращения случайностей, которые могут возникнуть в ходе выполнения работ. Если планировать выполнение работ по ранним срокам их начала и окончания, то всегда будет возможность при необходимости перейти на поздние сроки начала и окончания работ.

Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также «цепочек» пути. Более точным инструментом решения этой задачи по сравнению с полным резервом является коэффициент напряженности, который может быть вычислен одним из двух способов по формуле:

,
где - продолжительность максимального пути, проходящего через работу ; - продолжительность (длина) критического пути; 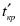- продолжительность отрезка рассматриваемого (максимального пути, проходящего через работу ) пути, совпадающего с критическим путем; - полный резерв времени работы

Коэффициент напряженности может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. Чем ближе коэффициент напряженности к 0, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.