
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка транспортной задачи общего видаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Классическая постановка транспортной задачи общего вида такова. вj – спрос j -го потребителя, j = 1,…, n; сij – стоимость перевозки одной единицы продукции из пункта Ai – i- го поставщика, в пункт Вj – j -го потребителя. Для наглядности данные удобно представлять в виде таблицы, которую называют таблицей стоимостей перевозок
Требуется найти план перевозок, при котором бы полностью удовлетворялся спрос всех потребителей, при этом хватало бы запасов поставщиков и суммарные транспортные расходы были бы минимальными. Ограничения задачи примут вид:
Это условие для решения закрытых и открытых транспортных задач (ЗТЗ).
Если это неравенство выполняется строго, то задача называется «открытой» или «несбалансированной», если же
Это условие для решения закрытых транспортных задач (ЗТЗ). В силу ограничений (2) нетрудно увидеть, что ЗТЗ является задачей ЛП и может быть решена симплекс-методом после приведения ее к специальному виду. Но структура системы ограничений имеет некоторою специфику, а именно: каждая переменная хij входит ровно два раза в неравенства системы, и все переменные входят в неравенства системы с коэффициентом 1. В силу этой специфики существует более простой метод решения, называемый методом потенциалов, который, по сути, является некоторой модификацией симплекс-метода. По-прежнему идеей является переход от одного опорного плана к другому, обязательно «лучшему» с точки зрения значения целевой функции. Каждому опорному плану также соответствует своя распределительная таблица. Переход осуществляется от одного плана к другому, пока полученный план не будет удовлетворять условию оптимальности. Необходимо научиться строить первоначальный опорный план. В качестве первоначального плана годится любое решение системы уравнений (2). Заметим, что это система линейных уравнений, состоящая из m + n уравнений с m*n неизвестными. Можно доказать, что линейно независимых уравнений в системе (2) m + n – 1, ввиду условия сбалансированности, т.е. базисных переменных должно быть m + n – 1. Итак, в качестве плана будем представлять себе таблицу размера m ∙ n, в которой должно быть занято m + n – 1 клеток, отвечающих базисным переменным xij. Транспортные задачи с неправильным балансом В рассмотренной модели транспортной задачи мы предполагали, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е. Такая задача называется задачей с правильным балансом, а ее модель — закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель — открытой. Решение задачи с неправильным балансом сводится к решению задачи с правильным балансом введением в ее математическую модель фиктивного поставщика или фиктивного потребителя. Тарифы на перевозку грузов от таких поставщиков или к таким потребителям полагаются равными 0 (т.е. фактически соответствующие перевозки не производятся). В случае превышения общего запаса продукции над потребностью, т.е. если в рассмотрение вводится фиктивный потребитель с потребностью с тарифами на перевозку c(n +1)j=0. Этим приемом задача сводится к закрытой транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи. Заметим, что при составлении начального опорного решения для ускорения вычислений в последнюю очередь следует (хотя и не обязательно) распределять запасы фиктивного поставщика и удовлетворять запросы фиктивного потребителя, несмотря на то, что им соответствуют наименьшие тарифы на перевозку (равные 0). Сведение транспортной постановки к задаче линейного программирования. СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА И ФОРМАЛЬНАЯ МОДЕЛЬ ТЗЛП Пусть имеется m пунктов производства однородной или взаимозаменяемой продукции. Каждый из пунктов производства обозначим через, где i= 1,...,m. Через будем обозначать объем продукции, производимой в пункте. И пусть имеется n пунктов потребления (назначения) данной продукции, каждый из которых будем обозначать, где j=1,...,n, а через будем обозначать объем потребления (спроса) продукции в пункте. Стоимость перевозки единицы продукции от i-го производителя к j-му потребителю составляет (i=1,...,m, j=1,...,n). Предполагается, что транспортные расходы на перевозки между любой парой пунктов пропорциональны объему перевозимого продукта. Требуется установить такие объемы перевозок от каждого производителя к каждому потребителю, чтобы суммарные затраты на перевозки были минимальными и потребности всех потребителей были бы удовлетворены (если только объем возможных поставок покрывает общий объем потребления). Представим транспортную модель в виде сети. В ней: вершины соответствуют пунктам производства и потребления, дуги, соединяющие вершины, представляют собой маршруты, по которым перевозится продукция, вес дуги – расстояние между соотв. пунктами. 16. Методы построения первого опорного плана транспортной задачи: метод северо-западного угла, метод минимальных элементов, метод штрафов (алгоритм Фогеля). 1)Метод северо-западного угла. Следуя этому методу, начинают с того, что приписывают неизвестной Пусть условия транспортной задачи заданы таблице 2.3. Таблица 2.3
У поставщика А2 осталось 150 ед. груза. Удовлетворяем потребителя B2 за счет оставшегося у поставщика А2 груза. Для этого сравниваем этот остаток с потребностями потребителя B2: 150<200, записываем 150 ед. в клетку А2B2 и, так как запасы А2 полностью израсходованы, прочеркиваем остальные клетки второй строки. Потребности B2 остались неудовлетворенными на 50 ед. Удовлетворяем их за счет поставщика А3 и переходим к удовлетворению B3 за счет остатка, имеющегося у поставщика А3, и т. д. Процесс продолжаем до тех пор, пока не удовлетворим всех потребителей за счет запасов поставщиков. На этом построение первоначального опорного плана заканчивается. Найдем общую стоимость составленного плана как сумму произведений объемов перевозок, стоящих в левом углу занятых клеток, на соответствующие стоимости в этих же ячейках: Z = 100 *10 + 100*2 + 150 *7+ 50 *5 + 100*3 + 50*2 + 50*16+ 250*13 = 6950 (eд. стоимости) 2) Метод наименьшей стоимости. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Составим с помощью этого метода опорный план уже рассмотренной задачи. Запишем ее условие в таблицу (табл. 2.5). Выбираем в таблице наименьшую стоимость (это стоимость, помещенная в клетке A1, B4) так как A1 = b4, 100 ед. груза помещаем в этой клетке и исключаем из рассмотрения первую строку и четвертый столбец. В оставшейся таблице стоимостей наименьшей является стоимость, расположенная в клетке A2 , B1 и в клетке A3 , B5. Заполняем любую из них, например A2 , B1. Имеем 200 < 250, следовательно, записываем в нее 200 и исключаем из рассмотрения столбец B1. В клетку A3 , B5 записываем 200 ед. и исключаем из рассмотрения строку A3 . В оставшейся таблице стоимостей снова выбираем наименьшую стоимость и продолжаем процесс до тех пор, пока все запасы не будут распределены, а потребности удовлетворены. В результате получен план Таблица 2.5
План не содержит циклов и состоит из семи положительных перевозок, следовательно, является вырожденным опорным планом. Определим его стоимость: 3).Метод аппроксимации Фогеля Данный метод состоит в следующем: на каждой итерации находят разности между двумя наименьшими тарифами во всех строках и столбцах, записывая их в дополнительные столбец и строку таблицы; находят max Δcij и заполняют клетку с минимальной стоимостью в строке (столбце), которой соответствует данная разность. Процесс продолжается до тех пор, пока все грузы не будут развезены по потребителям. Данный метод в ряде задач приводит к оптимальному плану. Решим этим методом задачу из примера 2.6.1 (см. табл.2.7).
На первом шаге заполняем клетку A3 B1 (max Δc = 5 и min cij = 6), исключаем 1-ый столбец, отметив в дополнительной строке буквой «В» факт выполнения заказа пункта B1 . Находим новые разности минимальных тарифов по строкам (в столбцах они не изменились) и max Δc = 2 в 1-ой строке и в 4-ом столбце. Заполняем клетку A1B4 и исключаем 4-й столбец и т.д. В конце остается последовательно заполнить клетки 3-го столбца остатками запасов в A1 , A3 , A2 . Составленный опорный план дает значение Z3 = 909 < Z2. Распределительный метод Один из наиболее простых методов решения транспортных задач - распределительный метод. Пусть для транспортной задачи найдено начальное опорное решение Х1 и вычислено значение целевой функции на этом решении F(Х1). По доказанной выше теореме для каждой свободной клетки таблицы задачи можно построить единственный цикл, который содержит эту клетку и часть клеток, занятых опорным решением. Обозначив этот цикл и осуществив сдвиг (перераспределение груза) по циклу на величину Определим, как изменится целевая функция при переходе к новому опорному решению. При сдвиге на единицу груза по циклу, соответствующему клетке (l,m), приращение целевой функции Δlm равно разности двух сумм:
где Если разность сумм для свободной клетки (l, m) меньше нуля, т.е. Δ lm< 0, то перераспределение величины θ по соответствующему циклу приведет к уменьшению значения F(X) на величину θ • Δlm, т.е. опорное решение можно улучшить. Если же величины Δlm, называемые оценками, для всех свободных клеток таблицы транспортной задачи неотрицательны, то значение целевой функции нельзя уменьшить и опорное решение оптимально. Следовательно, признаком оптимальности распределительного метода является условие
Для каждого нового опорного решения вычисление оценок начинается с первой свободной клетки таблицы. Очередность проверяемых свободных клеток целесообразно устанавливать в порядке возрастания стоимости перевозок cij,так как решается задача на нахождение минимума. ПРИМЕР. Решить распределительным методом транспортную задачу, исходные данные которой приведены в таблице:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.233 (0.011 с.) |


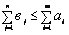
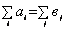 , то задача называется «закрытой» транспортной задачей, и будет иметь вид (2):
, то задача называется «закрытой» транспортной задачей, и будет иметь вид (2):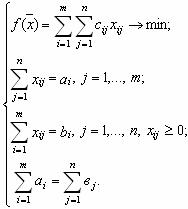
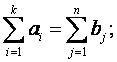
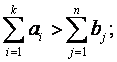

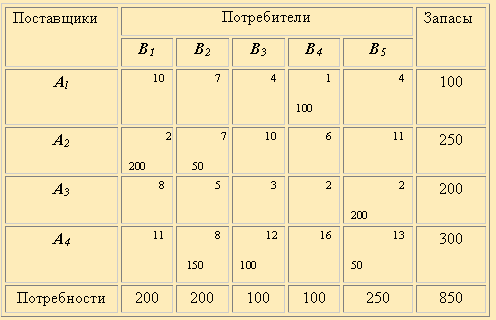
 то вводится фиктивный поставщик, запасы которого равны
то вводится фиктивный поставщик, запасы которого равны 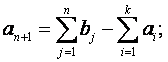
 (расположенной в северо-западном углу таблицы) максимальное значение, допускаемое ограничениями на спрос и объем производства. После этого вычеркивают соответствующий столбец (или строку), фиксируя этим, что остальные неизвестные вычеркнутого столбца (строки) полагаются равными нулю. Если ограничения, представляемые столбцом и строкой, выполняются одновременно, то можно вычеркнуть либо столбец, либо строку (это условие автоматически гарантирует обнаружение нулевых базисных переменных, если таковые встречаются). После того спрос и объем производства во всех невычеркнутых строках и столбцах, приведены в соответствие с установленным значением переменной, максимально допустимое значение приписывается первому невычеркнутому элементу нового столбца (строки). Процесс завершается, когда остается невычеркнутой в точности одна строка (или один столбец).
(расположенной в северо-западном углу таблицы) максимальное значение, допускаемое ограничениями на спрос и объем производства. После этого вычеркивают соответствующий столбец (или строку), фиксируя этим, что остальные неизвестные вычеркнутого столбца (строки) полагаются равными нулю. Если ограничения, представляемые столбцом и строкой, выполняются одновременно, то можно вычеркнуть либо столбец, либо строку (это условие автоматически гарантирует обнаружение нулевых базисных переменных, если таковые встречаются). После того спрос и объем производства во всех невычеркнутых строках и столбцах, приведены в соответствие с установленным значением переменной, максимально допустимое значение приписывается первому невычеркнутому элементу нового столбца (строки). Процесс завершается, когда остается невычеркнутой в точности одна строка (или один столбец).

 можно получить новое опорное решение Х2.
можно получить новое опорное решение Х2.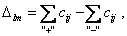
 - сумма стоимостей перевозок единиц груза в нечетных клетках цикла, отмеченных знаком “+”;
- сумма стоимостей перевозок единиц груза в нечетных клетках цикла, отмеченных знаком “+”; 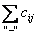 - сумма стоимостей перевозок единиц груза в четных клетках цикла, отмеченных знаком “-”.
- сумма стоимостей перевозок единиц груза в четных клетках цикла, отмеченных знаком “-”. 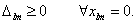
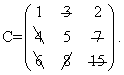
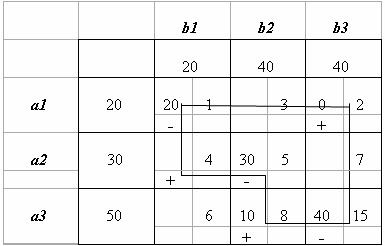
 Приращение целевой функции ΔF=-7∙20=-140. Получим новое опорное решение X2. Значение целевой функции на нем F(X2)=20∙2+20∙4+10∙5+30∙8+20∙15=710.
Приращение целевой функции ΔF=-7∙20=-140. Получим новое опорное решение X2. Значение целевой функции на нем F(X2)=20∙2+20∙4+10∙5+30∙8+20∙15=710. 
 . Приращение целевой функции ΔF=-5∙10=-50. Получаем третье опорное решение X3. Значение целевой функции на нем F(X3)=20∙2+20∙4+10∙7+40∙8+10∙15=660.
. Приращение целевой функции ΔF=-5∙10=-50. Получаем третье опорное решение X3. Значение целевой функции на нем F(X3)=20∙2+20∙4+10∙7+40∙8+10∙15=660. 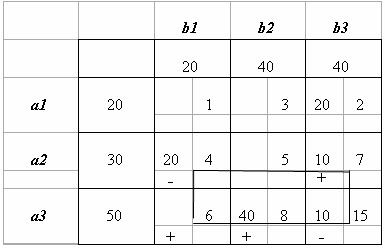
 Приращение целевой функции ΔFm=-6∙10=-60. Получаем четвертое опорное решение X4 Значение целевой функции на нем F(X4)=20 ∙2+10∙4+20∙7+10∙6+40∙8=600.
Приращение целевой функции ΔFm=-6∙10=-60. Получаем четвертое опорное решение X4 Значение целевой функции на нем F(X4)=20 ∙2+10∙4+20∙7+10∙6+40∙8=600. 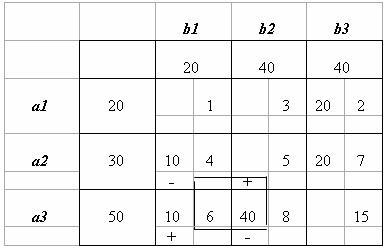
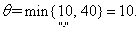 Приращение целевой функции ΔF=-1∙10=-10. Получаем пятое опорное решение X5.
Приращение целевой функции ΔF=-1∙10=-10. Получаем пятое опорное решение X5. 



