
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Транспортные задачи. Блокирование. Распределительные задачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если план транспортной задачи Х= +— Модель транспортной задачи закрытая, если +— Цикл в транспортной задаче – это +—замкнутая ломаная линия с горизонтальными и вертикальными звеньями, одна вершина которой в свободной клетке, а остальные в занятых клетках
План транспортной задачи называется вырожденным, если число загруженных клеток +—меньше m+n-1
Модель транспортной задачи является открытой, если +— Потенциалами транспортной задачи размерности (mxn) называются m+n чисел ui и vj, для которых выполняются условия +—ui+vj=cij для занятых клеток
Оценками транспортной задачи размерности +—для свободных клеток
Целевая функция транспортной задачи имеет вид +— При составлении первоначального плана транспортной задачи по методу минимальной стоимости в первую очередь заполняются клетки +—с минимальными тарифами
При решении транспортной задачи значение целевой функции должно от итерации к итерации +—уменьшаться или не меняться
В клетках распределительной таблицы транспортной задачи располагаются +—планы перевозок xij и соответствующие тарифы cij
Если план транспортной задачи X=(xij)mЧn является оптимальным, то оценки +—гij
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид
Чтобы произвести блокировку некоторой клетки транспортной задачи, в этой клетке тариф +—изменяют на достаточно большое число
Число занятых клеток любого невырожденного плана транспортной задачи должно быть равно +—m+n-1
Экономический смысл целевой функции транспортной задачи +—суммарная стоимость перевозок В целевой функции транспортной задачи +—стоимость перевозки одной тонны груза от i–ого поставщика к j–ому потребителю В целевой функции транспортной задачи +—объем груза от i–ого поставщика к j–ому потребителю В транспортной задаче сумма потенциалов ui+vj равна тарифу cij, +—занятых клеток
В транспортной задаче оценки гij вычисляются для +—для незанятых клеток
В транспортной задаче +—минимизируется общая стоимость перевозок Элементы матрицы производительностей +—шт/час Элементы матрицы затрат +—руб/шт
В таблице задачи о загрузке оборудования каждая клетка содержит +—производительность станка, затраты на один час работы станка, время работы над j-ым изделием
В задаче о загрузке оборудования +—фонды рабочего времени станков
В задаче о загрузке оборудования b1, b2,…,bn – это +—заказ по выпуску изделий в штуках
В задаче о загрузке оборудования +— В задаче о загрузке оборудования +—индексом i–ого станка
В задаче о загрузке оборудования
+—приведенными к стандартным часам потребностями
В задаче о загрузке оборудования
+—приведенными к стандартным часам затратами В задаче о загрузке оборудования +—приведенным к стандартным часам фондом рабочего времени станков В +—приведенное время работы i – го станка по производству
Дан план транспортной задачи
Неоптимальной будет клетка +—(1,1)
Дан план транспортной задачи
Этот план +—вырожденный
Дан план транспортной задачи
Неоптимальной будет клетка +—(3,3)
Дана транспортная задача
Первоначальный план, найденный методом минимальной стоимости, имеет вид
Дан план транспортной задачи
Значение целевой функции равно +—750
Дан план транспортной задачи
этот план +—невырожденный
Дан план транспортной задачи
Цикл нужно строить для клетки +—(1,1)
Дана транспортная задача
План, найденный методом минимальной стоимости, имеет вид
Дана транспортная задача и дополнительное условие: третий поставщик должен полностью отправить свой груз.
Необходимо заблокировать клетку +—(3,3)
Дана транспортная задача c дополнительным условием, что перевозки от второго поставщика к третьему потребителю запрещены.
Необходимо заблокировать клетку +—(2,3)
Дана транспортная задача c дополнительным условием, что первый потребитель должен получить груз полностью.
Необходимо заблокировать клетку +—(4,1) В задаче по загрузке оборудования индекс +— В задаче по загрузке оборудования элементы матрицы +—производительность
Оптимальный план транспортной задачи будет единственным, если для свободных клеток оценки +— — Дана транспортная задача
Первоначальный план, найденный методом минимальной стоимости, имеет вид
Дан план транспортной задачи
Потенциалы поставщиков и потребителей
План транспортной задачи
+—оптимальный и неединственный
План транспортной задачи
+—оптимальный и единственный
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид
Экономически отрицательная оценка +—уменьшится на Оценки транспортной задачи, вычисляемые для свободных клеток, находятся по формуле +— Блокирование перевозок применяется для клетки +—перевозки запрещены Если все оценки для свободных клеток +—оптимальным Блокирование перевозок применяется в транспортной задаче с открытой моделью. Если +—быть вывезен полностью Блокирование перевозок применяется в транспортной задаче с открытой моделью. Если +—удовлетворяться полностью Если плану транспортной задачи +—оптимальным
В транспортной задаче для плана, приведенного в таблице
неоптимальной клеткой будет +—(1,2)
В транспортной задаче для плана, приведенного в таблице
неоптимальной клеткой будет +—(3,1) Если модель транспортной задачи открытая и +—фиктивный потребитель с тарифами, равными 0
Дан план транспортной задачи и вычислены потенциалы:
Данный план является +—оптимальным
Дана транспортная задача:
с открытой моделью. После приведения к закрытой модели она примет вид
Дана транспортная задача:
После приведения к закрытой модели она примет вид
Если в транспортной задачи +—фиктивного поставщика с тарифами, равными 0 Если в оптимальном плане транспортной задачи хотя бы одна оценка +—он неединственный
Дан план транспортной задачи и определены потенциалы:
Данный план +—оптимальный
Чтобы данный вырожденный план транспортной задачи
сделать невырожденным, нельзя поместить нулевую перевозку в клетку +—(1;3)
Данный план транспортной задачи
является +—вырожденным
Если в плане транспортной задачи число занятых клеток на единицу меньше +—одну клетку занимают нулевой перевозкой
Тема 9. Сетевое планирование и управление Реальная работа - это +—работа, требующая затрат ресурсов и времени Полный резерв времени +— Конечное событие сетевого графика – это +—событие, не имеющее выходящих работ
Начальное событие сетевого графика – это событие +—не имеющее входящих работ Временной параметр +—самый ранний срок начала работы Параметр +—полный резерв времени на работу
Работа – ожидание +—требует только время —требует только ресурсы
Событие n-го ранга (n¹1) – это событие +—в которое входит работа, отмеченная наибольшим номером, равным (n-1) и ниже
Критическим путем называется +—путь наибольшей длины из начального события в конечное событие
Наиболее ранний срок наступления события с номером k вычисляется по формуле +— Параметр tij – это +—время, необходимое для выполнения работы Aij —время, необходимое для наступления события с номером i
Фиктивная работа +—не требует ни времени, ни ресурсов
Необходимым и достаточным условием того, что работа лежит на критическом пути, является +—Rijп=0 Временной параметр +—самый ранний срок окончания работы Временной параметр +—поздний срок окончания работы
Направление стрелок работ в сетевом графике изображается +—слева направо
Длиной пути из события i в событие j называется +—сумма продолжительностей работ, составляющих этот путь
Математическим аппаратом сетевого планирования и управления является теория +—графов
Если несколько работ выходят из одного события и заканчиваются в другом, то для их различия нужно ввести +—фиктивные работы —фиктивные события
В сетевом графике не должно быть: —фиктивных работ—работ – ожиданий—фиктивных событий +—циклов
Работа, требующая только время, называется +—работой – ожидание
Работа, не требующая ни времени, ни ресурсов, называется +—фиктивной
Работа, потребляющая ресурсы и время, называется +—реальной работой
Сетевой график состоит из +—работ и событий —работ и их длительностей
Событие сетевого графика изображается +—кружком
Работа изображается на сетевом графике +—стрелкой
Событие свершилось, если +—выполнены все работы, в него входящие При обозначении работы +— Работы, выходящие из событий n –го ранга, имеют номер —n-1 +—n —n+1 —n+2
Величина +—длине наибольшего пути от события j до конечного события
Максимальное время, за которое необходимо выполнить данный комплекс работ, равно +—длине критического пути
При нумерации событий сетевого графика необходимо определить +—ранг событий
Сетевой график может иметь +—одно начальное и одно конечное событие
Раннее время свершения k – го события вычисляется по формуле +— Поздний срок окончания работы +— Событие, в которое входит работа с номером III, будет событием +—четвертого ранга
Событие, в которое входят работы с номерами V и I, будет событием +—шестого ранга
Событие, в которое входят работы с номерами V и VII, будет событием +—восьмого ранга
Работе, выходящей из события шестого ранга присваивают номер +—VI
В сетевом графике число событий и работ должно быть +—счетным (натуральные)
Целью системы сетевого планирования управления является +—выявление и мобилизация резервов времени
Сетевой моделью называется ЭММ, отображающая +—комплекс работ и событий, связанных с реализацией некоторого проекта
Графом называется +—совокупность точек, называемых вершинами, и ориентированных дуг, соединяющих вершины
Сетью называется —совокупность событий и работ +—граф, в котором только одна точка, не имеющая входящих дуг, и лишь одна точка, не имеющая выходящих дуг, и каждой дуге которого приписано число В сетевом графике путем из начального события +—последовательность работ, в которой конец каждой предыдущей работы совпадает с началом последующей
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 1242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.031 с.) |

 является оптимальным, то ему соответствует система
является оптимальным, то ему соответствует система  чисел, называемых потенциалами, для которых выполняются следующие условия
чисел, называемых потенциалами, для которых выполняются следующие условия для
для  ,
,  для
для 


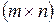 называются числа гij, которые вычисляются
называются числа гij, которые вычисляются
 удовлетворяют условиям
удовлетворяют условиям 0 для свободных клеток
0 для свободных клеток коэффициенты cij – это
коэффициенты cij – это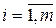 ,
,  для
для в
в  - задаче имеют размерность
- задаче имеют размерность в
в 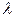 - задаче имеют размерности
- задаче имеют размерности – это
– это
 называется
называется (
( )называются
)называются (
( ) называются
) называются называются
называются - это
- это - го вида изделий
- го вида изделий


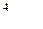
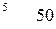



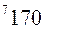
















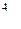
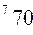


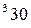



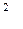
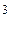



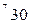


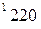




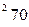








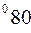





















 - го станка
- го станка  определяется по формуле
определяется по формуле
 - это
- это





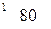






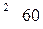
 соответственно равны
соответственно равны
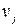



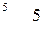









 показывает что, если в клетку
показывает что, если в клетку  перебросить 1т груза, то суммарная стоимость перевозки
перебросить 1т груза, то суммарная стоимость перевозки

 , то план транспортной задачи будет
, то план транспортной задачи будет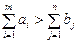 , то накладывается дополнительное условие, что груз i – го поставщика должен
, то накладывается дополнительное условие, что груз i – го поставщика должен , то вводится дополнительное условие, что потребности j – го потребителя должны
, то вводится дополнительное условие, что потребности j – го потребителя должны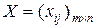 соответствует система m+n чисел (потенциалов), для которых выполняются условия
соответствует система m+n чисел (потенциалов), для которых выполняются условия  для
для 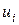





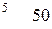



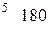


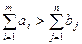 , то вводится
, то вводится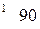
















 , то для приведения к закрытой модели следует вводить
, то для приведения к закрытой модели следует вводить , то
, то

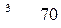


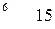



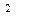
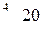


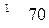







 , то
, то вычисляется по формуле
вычисляется по формуле
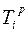 - это
- это
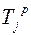 - это
- это - это
- это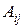 на сетевом графике
на сетевом графике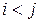
 равна
равна
 вычисляется по фоормуле
вычисляется по фоормуле
 в конечное
в конечное  называется
называется


