
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Решение систем линейных уравнений методом Жордана – ГауссаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общим решением системы m линейных уравнений с n неизвестными называется +—решение, в котором базисные неизвестные линейно выражаются через свободные неизвестные
Частным решением системы m линейных уравнений с n неизвестными называется +—решение, полученное из общего решения, если свободным неизвестным придать произвольные значения
При отыскании общего решения системы m линейных уравнений с n неизвестными методом Жордана – Гаусса в качестве разрешающего элемента выбирается +—любой отличный от нуля элемент таблицы, кроме элементов столбца свободных членов и контрольного столбца
Система m линейных уравнений с n неизвестными не имеет решений, если на некоторой итерации +—все элементы какой – либо строки таблицы Жордана – Гаусса, кроме свободного члена, равны нулю
Базисным решением системы m линейных уравнений с n неизвестными называется +—решение, полученное из общего решения системы, в котором свободные неизвестные равны 0
Если r – число базисных неизвестных, а n – общее число неизвестных в произвольной системе m линейных уравнений, то система имеет бесконечное множество решений при +—
Если дано матричное уравнение +— Если в таблице Жордана – Гаусса +— Итерацией в методе Жордана - Гаусса называется +—расчет элементов одной таблицы Жордана – Гаусса
Метод Жордана – Гаусса это +—последовательное исключение неизвестных
Если в таблице Жордана – Гаусса имеются две одинаковые строки, то +—одну из них можно вычеркнуть
Единичным называется столбец таблицы Жордана – Гаусса, который состоит из +—одной единицы и остальных 0
Переменная называется базисной, если в таблице Жордана – Гаусса столбец коэффициентов перед ней является +—единичным
Если в таблице Жордана – Гаусса имеются две пропорциональные строки, то +—одну из них нужно вычеркнуть
Переменная называется свободной, если в таблице Жордана – Гаусса +—она не входит в столбец в базис
Система m линейных уравнений с n неизвестными называется однородной, если свободные члены +—равны 0
Матрица коэффициентов при неизвестных системы m линейных уравнений с n неизвестными +—прямоугольной
Число частных решений равно +—бесчисленному множеству решений
Переход от одного базисного решения к другому осуществляется путем +—проведения еще одной итерации метода Жордана – Гаусса
Элементы вводимой строки в таблице Жордана – Гаусса находятся +—делением элементов разрешающей строки предыдущей таблицы на разрешающей элемент
Число базисных решений произвольной системы m линейных уравнений с n неизвестными определяется +—формулой
Решение системы m линейных уравнений с n неизвестными, в котором базисные неизвестные линейно выражаются через свободные, называется +—общим
Систему можно решить матричным способом, если +—число уравнений равно числу неизвестных
Решение, полученное из общего решения, если свободным неизвестным придать произвольные значения, называется +—частным
Значение базисных переменных в таблице Жордана – Гаусса находится в +—столбце
В контрольный столбец 1-й таблицы Жордана – Гаусса записывается +—сумма элементов по каждой строке, включая свободные члены
Матрица коэффициентов при неизвестных при решении системы n линейных уравнений с n неизвестными матричным способом является +—невырожденной
При решении системы m линейных уравнений с n неизвестными методом Жордана – Гаусса контроль вычислений в таблицах Гаусса, начиная со 2 –ой, проводится путем +—сравнения суммы элементов по каждой строке, включая свободные члены, с элементами контрольного столбца
В столбце +—базисных
Решение системы линейных уравнений с n неизвестными находится с применением обратной матрицы, если число уравнений равно +—n
Решение, матричного уравнения находится по формуле +— Решение, полученное из общего решения, если свободным неизвестным придать нулевые значения называется +—базисным
Если в таблице Жордана – Гаусса все элементы какой – либо строки, кроме свободного члена, равны нулю, то система m линейных уравнений с n неизвестными +—не имеет решений
Если в системе m линейных уравнений с n неизвестными +—бесчисленное множество решений
Если при решении системы m линейных уравнений c n неизвестными в разрешающей строке таблицы Жордана – Гаусса находится нуль, то столбец, содержащий этот нуль +—переносится в следующую таблицу без изменения
Если в базисном решении системы линейных уравнений Если в базисном решении системы линейных уравнений
Если в системе m линейных уравнений с n неизвестными +—неопределенной
Если в системе m линейных уравнений с n неизвестными +—переопределенной
В системе m линейных уравнений с n неизвестными число базисных решений равно +— Если в базисном решении системы линейных уравнений Если в базисном решении системы линейных уравнений Если в базисном решении системы линейных уравнений Если в базисном решении системы линейных уравнений Если в базисном решении системы линейных уравнений Если в базисном решении системы линейных уравнений Если в базисном решении системы линейных уравнений
Если разрешающим элементом в преобразованиях однократного замещения является В системе линейных уравнений +—(0,5,0,3)
|
||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 1749; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.135 (0.011 с.) |


 , то его решение определяется по формуле
, то его решение определяется по формуле
 - разрешающий элемент, то элемент
- разрешающий элемент, то элемент  находится по формуле (правило прямоугольника)
находится по формуле (правило прямоугольника)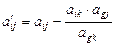

 является
является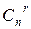

 , если оно имеет вид
, если оно имеет вид
 - число базисных неизвестных и при этом
- число базисных неизвестных и при этом 
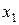 ,
,  − базисные переменные, то
− базисные переменные, то  равно +—30
равно +—30
 − базисные переменные, то
− базисные переменные, то  равно +—16
равно +—16 , то система называется
, то система называется , то система называется
, то система называется

 равно +—6
равно +—6

 равно +—0
равно +—0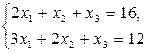
 равно +—12
равно +—12
 равно +—12
равно +—12
 равно +—-4
равно +—-4
 − базисные переменные, то
− базисные переменные, то  равно +—2
равно +—2 , то новые элементы
, то новые элементы  в таблице Гаусса определяются по формуле +—
в таблице Гаусса определяются по формуле +— 
 базисное решение имеет вид
базисное решение имеет вид


