
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Малые колебания произвольной системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для упрощения рассуждений ограничимся рассмотрением одномерного случая и рассмотрим систему, положение которой может быть задано с помощью одной координаты
(отметим, что определение малых колебаний фактически в том и заключается, что при совершении колебаний система отклоняется от положения равновесия настолько мало, что зависимость ее потенциальной энергии от координаты с достаточной, в рассматриваемой задаче, точностью выражается соотношением (5.1).) Вследствие того, что потенциальная энергия системы определена с точностью до произвольной константы, примем, что в положении равновесия она равна нулю: В положении устойчивого равновесия потенциальная энергия имеет минимум. Поэтому первая производная должна быть равна нулю в точке равновесия:
Обратите внимание на то, что соотношение (5.2) аналогично выражению для потенциальной энергии деформированной пружины. Соответственно сила, действующая на систему, описывается формулой:
Очевидно, что формула (5.3) аналогично закону Гука, поэтому силы, описываемые соотношением типа (5.3), независимо от их природы называют квазиупругими. Единственное ограничение, которое мы сделали при получении соотношения (5.3) заключалось в предположении о малости отклонений от положения равновесия. Даже вид функции Рассмотрим движение системы под действием только квазиупругой силы (считаем, что силы сопротивления движению отсутствуют!). Если масса системы равна
Разделив уравнение (5.4) на
где использовано обозначение Итак, если система находится под воздействием только квазиупругой силы, то ее движение описывается дифференциальным уравнением (5.5). Таким уравнением описывается движение шарика на рисунке 5.1, груза, подвешенного на пружине, маятников и многих других систем. Для всех таких систем существует общее название: гармонический осциллятор. Название связано с тем, что такие системы совершают простейшие, гармонические колебания. Немного ниже мы рассмотрим этот вопрос подробней. Вполне очевидно, что гармонический осциллятор представляет собой абсолютную идеализацию и в чистом виде не встречается. Во всякой реальной колебательной системе обязательно действуют силы
В этом случае в уравнение движения необходимо добавить силу сопротивления, и оно принимает вид:
Тогда дифференциальное уравнение, описывающее движение в этом случае, будет иметь вид:
где Если на систему кроме квазиупругой действуют диссипативные силы, то она совершает свободные колебания. Таким образом, свободные колебания системы описываются дифференциальным уравнением (5.8). Очень часто встречаются ситуации, когда система совершает вынужденные колебания под действием внешней периодической силы. В простейшем случае внешняя сила изменяется по закону
где Уравнения (5.5), (5.8) и (5.9) являются линейными дифференцированными уравнениями с постоянными коэффициентами. Для их решения в математике разработан специальный метод, который изложен не только в учебниках по математике, но и во многих учебниках по физике. Изучить (или вспомнить) методику решения линейных дифференциальных уравнений этого вида необходимо самостоятельно. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ. Рассмотрим решение уравнения (5.5). Следуя известной технологии решения линейных дифференциальных уравнений, предположим, что решение уравнения (5.5) имеет вид
два корня, которого равны
Тогда общее решение уравнения (5.5) имеет вид:
где Воспользуемся тем, что функция, описывающая колебания реальной физической системы, должна быть вещественной, а значит, комплексно сопряженное выражение для смещения из положения равновесия должно совпадать с самим выражением:
Для выполнения соотношения (5.13) необходимо, чтобы были равны коэффициенты слева и справа перед выражениями
Представим комплексные числа
где Фактически мы заменяем произвольные константы При этих значениях констант
Преобразуем это соотношение по формуле Эйлера: для любого вещественного
Таким образом,
Отметим, что произвольные константы Таким образом, если система находится под действием только квазиупругой силы, то ее смещение из положения равновесия изменяется по закону sin( ωt + α) или cos( ωt + α), т.е. система совершает гармонические колебания. Вспомнимопределения: § § величину § § § § Рассмотрим как изменяются в процессе колебаний скорость и ускорение колеблющегося тела. Взяв от (5.17) производную по времени, получим уравнение, описывающее колебания скорости
Очевидно, что колебания скорости происходят с амплитудой Производная по времени от скорости дает зависимость ускорения от времени:
Очевидно, что изменение во времени ускорения на Каждое конкретное колебание, которое может совершать система, характеризуется определенными значениями амплитуды Колебания, которые совершает система под действием только квазиупругой силы называются собственными колебаниями. Отличительной особенностью собственных колебаний являются их гармонический характер, который подразумевает абсолютное постоянство амплитуды, частоты и фазы колебаний, причем частота колебаний определяется соотношением (5.5).
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 735; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 . Можно представить себе шарик (материальную точку), который катится по желобу. Желоб расположен в одной плоскости, а его высота изменяется при движении шарика. Потенциальная энергия шарика в поле силы тяжести будет тогда функцией одной переменной, определяющей положения шарика в желобе. Соответственно потенциальная энергия системы будет функцией одной переменной:
. Можно представить себе шарик (материальную точку), который катится по желобу. Желоб расположен в одной плоскости, а его высота изменяется при движении шарика. Потенциальная энергия шарика в поле силы тяжести будет тогда функцией одной переменной, определяющей положения шарика в желобе. Соответственно потенциальная энергия системы будет функцией одной переменной: 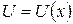 . В первом приближении будем считать, что силы сопротивления движению шарика отсутствуют.
. В первом приближении будем считать, что силы сопротивления движению шарика отсутствуют. Рассмотрим ситуацию вблизи положения устойчивого равновесия. Будем отсчитывать
Рассмотрим ситуацию вблизи положения устойчивого равновесия. Будем отсчитывать  в ряд в окрестности положения равновесия и ограничимся рассмотрением малых колебаний, т.е. малыми значениями
в ряд в окрестности положения равновесия и ограничимся рассмотрением малых колебаний, т.е. малыми значениями  можно пренебречь и считать, что в окрестности точки с координатой
можно пренебречь и считать, что в окрестности точки с координатой  :
: (5.1)
(5.1) . Поэтому первое слагаемое в разложении можно отбросить.
. Поэтому первое слагаемое в разложении можно отбросить. (условие экстремума), а вторая положительна:
(условие экстремума), а вторая положительна:  (условие минимума). Обозначим
(условие минимума). Обозначим  . Тогда зависимость потенциальной энергии от координаты можно представить в виде:
. Тогда зависимость потенциальной энергии от координаты можно представить в виде: (5.2)
(5.2) . (5.3)
. (5.3)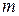 , то уравнение движения системы имеет вид:
, то уравнение движения системы имеет вид: . (5.4)
. (5.4) или
или (5.5)
(5.5) .
. сопротивления, которые приводят к диссипации механической энергии системы, причем чаще всего сила сопротивления оказывается пропорциональной скорости:
сопротивления, которые приводят к диссипации механической энергии системы, причем чаще всего сила сопротивления оказывается пропорциональной скорости: (5.6)
(5.6)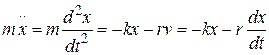 . (5.7)
. (5.7) или
или  (5.8)
(5.8) .
.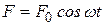 . Уравнение движения в этом случае примет следующий вид:
. Уравнение движения в этом случае примет следующий вид: или
или  (5.9)
(5.9) .
. . Подставив в уравнение это решение, получим характеристическоеуравнение:
. Подставив в уравнение это решение, получим характеристическоеуравнение: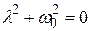 , (5.10)
, (5.10) ;
;  . (5.11)
. (5.11) (5.12)
(5.12) и
и 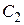 - комплексные константы, которые нам необходимо найти.
- комплексные константы, которые нам необходимо найти. , т.е.
, т.е. (5.13)
(5.13) и
и  :
: . (5.14)
. (5.14) в экспоненциальном виде (в показательной форме), а чтобы выполнялось условие (5.14) положим:
в экспоненциальном виде (в показательной форме), а чтобы выполнялось условие (5.14) положим: (5.15)
(5.15) и
и  - произвольные константы.
- произвольные константы. на (также произволдьные)
на (также произволдьные)  .
. .
. (5.16)
(5.16) (5.17)
(5.17) изменился по закону
изменился по закону  .
. - текущей фразой колебания,
- текущей фразой колебания,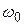 - круговой (циклической) частотой, (рад/с),
- круговой (циклической) частотой, (рад/с), - промежуток времени, через который движение системы повторяется, называют периодом колебания,
- промежуток времени, через который движение системы повторяется, называют периодом колебания, - частотой (Гц).
- частотой (Гц). системы:
системы: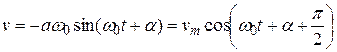
 , а текущая фаза колебаний на
, а текущая фаза колебаний на  больше, т.е. по фазе колебания скорости опережают колебания смещения на
больше, т.е. по фазе колебания скорости опережают колебания смещения на  . (5.18)
. (5.18)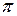 . Это означает, что смещение и ускорение при гармонических колебаниях изменяются в противофазе.
. Это означает, что смещение и ускорение при гармонических колебаниях изменяются в противофазе. и скорости
и скорости  системы в момент времени
системы в момент времени  . Для примера представим две ситуации. В первой маятник отклоняют от положения равновесия и в момент начала отсчета времени отпускают. В этом случае колебания будут описываться уравнением вида
. Для примера представим две ситуации. В первой маятник отклоняют от положения равновесия и в момент начала отсчета времени отпускают. В этом случае колебания будут описываться уравнением вида  . Если мысленно сместить начало отсчета времени на момент, когда маятник проходит положение равновесия, уравнение колебаний будет иметь вид
. Если мысленно сместить начало отсчета времени на момент, когда маятник проходит положение равновесия, уравнение колебаний будет иметь вид  .
.


