
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика вращательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
На правах рукописи Физика Конспект лекций (Часть1. Физические основы механики)
Для студентов направления 230400 «Информационные системы и технологии»
Электронный образовательный ресурс
Составитель: к.ф.-м.н., доцент В.В. Коноваленко
Рассмотрен и рекомендован для использования в учебном процессе на 2013/2014 – 2015/2016 уч. г. на заседании кафедры ЕНД. Протокол № 1 от 04. 09. 2013 г. Шахты 2013 КИНЕМАТИКА
ОСНОВНЫЕ ПОНЯТИЯ
Механическое движение – заключается в перемещении тел или их частей друг относительно друга и является простейшей формой движения материи. Рассматриваемой механической системой или просто – системой – будем называть совокупность тел, выделенных для рассмотрения. Говорить о движении отдельного тела в абсолютно пустом пространстве бессмысленно – всякое движение можно рассматривать только по отношению к другим телам. Кроме того, движение обязательно происходит во времени. Поэтому системой отсчета будем называть совокупность неподвижных друг относительно друга тел и отсчитывающих время часов. Количественное описание движения тела предполагает указание в каждый момент времени, его положения в пространстве и скорости. Чтобы иметь такую возможность с системой отсчета связывают некоторую систему координат (например, прямоугольную или декартову). Параметры, используемые для описания движения тел, способы описания движения виды движения тел без исследования причин, обусловливающих движение тела, рассматриваются в разделе механики, называемом кинематикой. Движение тел с учетом взаимодействий между ними изучается в разделе, называемом динамикой. При решении физических задач никогда невозможно получить абсолютно точного решения – всегда приходится пренебрегать некоторыми факторами, влияние которых в рассматриваемом случае несущественно. Такая же ситуация возникает при анализе или описании практически любого физического явления. При движении тел очень часто не имеют существенного значения размеры тела. Соответственно простейшей моделью реального тела, рассматриваемой в механике, является материальная точка (частица), которой, по определению, называют тело, размерами которого в условиях данной (!) задачи можно пренебречь. Во многих случаях при движении реального тела его деформации под действием других тел невелики. Поэтому второй важной моделью реального тела является абсолютно твердое тело – тело, деформациями которого в условиях данной (!) задачи можно пренебречь. В механике доказывается, что всякое движение тела можно представить в виде суммы двух основных видов движения: поступательного и вращательного (разложить на поступательное и вращательное). Поступательным, по определению, называется такое движение, при котором любая прямая, связанная с телом, остается параллельной самой себе. Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. ВЕКТОРЫ И ДЕЙСТВИЯ С НИМИ Многие физические величины (перемещение, скорость, сила, и т.д.) являются векторными, поэтому твердое знание основных сведений о векторах и действиях с ними является совершенно необходимой предпосылкой успешного изучения курса общей физики. Перечислим основные сведения о векторах, необходимые для дальнейшего:
В качестве примера действий с векторами рассмотрим производную по времени единичного вектора
При малом
(Гипотенуза треугольника – вектор Таким образом, представив
Необходимо учесть, что при
Забегая вперед, отметим, что по смыслу СКОРОСТЬ МАТЕРИАЛЬНОЙ ТОЧКИ Предварительно сформулируем необходимые определения (см. рисунок 1.2): Ø Ø Путь, пройденный материальной точкой – скалярная величина, равная расстоянию, отсчитанному вдоль траектории при движении частицы из некоторой точки 1 в точку 2, Ø
 , проведенный из точки 1 в 2 траектории. Очевидно, что перемещение , проведенный из точки 1 в 2 траектории. Очевидно, что перемещение  . С другой стороны разность конечного и начального значения радиус-вектора есть его приращение: . С другой стороны разность конечного и начального значения радиус-вектора есть его приращение:  . Поэтому можно считать, что можно считать, что перемещение представляет собой приращение радиус-вектора. . Поэтому можно считать, что можно считать, что перемещение представляет собой приращение радиус-вектора.
Движение частицы называется равномерным, если в любые равные промежутки времени частца проходит одинаковые пути (независимо от формы траектории!). Важнейшим понятием кинематики является скорость материальной точки. На качественном уровне под скоростью в физике понимают векторнуювеличину, характеризующую быстроту перемеще-ния частицы по траектории и направление, в котором движется частица. На бытовом уровне скорость можно найти, разделив путь, пройденный телом
и траекторию можно считать состоящей из элементов Поэтому по определению скоростью частицы называется производная ее радиус-вектора по времени:
Поскольку модуль приращения радиус-вектора за время
Учитывая, что выражение для радиус-вектора через его проекции на оси координат имеет вид
Как следует из соотношения (1.7), проекции вектора скорости на оси координат равны производным по времени проекций радиус-вектора, а составляющие вектора скорости по осям координат получаются умножением соответствующих производных на орты осей системы координат:
(Напомним: проекции – это алгебраические скалярные величины, составляющие – это векторы, которые в сумме дают данный вектор). В соответствии со своим определением вектор скорости характеризует быстроту изменения радус-вектора частицы. Радус-вектор
Находя производную по времени от этого выражения, получаем:
Составляющая
где
При движении точки изменяется ее радус-вектор
Таким образом, производная пути по времени дает модуль вектора скорости:
ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ Найдем общую формулу для вычисления пройденного частицей пути S в промежутке времени от
C геометрической точки зрения каждое из слагаемых в соотношении (1.15) представляет собой площадь прямоугольника высотой
Выражение (1.16) представляет собой определенный интеграл от
При этом геометрически пройденный путь изображается площадью, ограниченной графифком Если в соотношение (1.17) вместо
даст перемещение частицы за СРЕДНИЕ ЗНАЧЕНИЯ Традиционно (в быту) средней скоростью называют среднее значение модуля вектора скорости, которое, по определению, равно отношеню всего пути S, пройденного телом за некоторый промежуток времени
Эту величину называют также средней путевой скоростью. Соотношение (1.19) есть результат применения общей формулы для нахождения среднего значения скалярной или векторной функции
В частном случае, подставив в (1.20) в качестве
Не следует путать понятие средней скорости частицы (1.19) со средним значением скорости для совокупности одинаковых объектов, например среденй скорости молекул, средней скорости автомобилей данного таксопарка в некоторый момент времени и т.п. Ускорение Ускорением называют векторную величину, характеризующую быстроту изменения вектора скорости, и количественно определяемую соотношением
Поскольку скорость
Направление составляющей Составляющая Обсудим более подробно чем определяется нормальное ускорение. Легко понять, что быстрота изменения направления вектора скорости, а значит и нормального ускорения, будет тем больше, чем сильнее искривлена траектория и чем больше модуль скорости перемещения частицы по траектории. Для количественной характеристики степени скривленности траектории используется величина, называемая кривизной траектории:если при перемещении вдоль траектории на расстояние
Величина R, обратная кривизне, Гласно формуле (1.3)
. где Путь который проходит частица за время
С другой стороны – Приравнивая правые части этих соотношений, находим:
Тогда в соответствии с (1.23) Для для нормального ускорения получаем:
Полное ускорение
Лекция № 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ ЗАКОНЫ НЬЮТОНА Первый закон утверждает: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения (говорят также, сохраняет состояние своего движения) до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Этот закон выполняется не во всех системах отсчета. Действительно: что если есть две системы отсчета, движущиеся друг относительно друга с ускорением, то первый закон не может одновременно выполняться в обеих системах отсчета. Системы отсчета, в которых первый закон выполняется, называются инерциальными. Экспериментально с очень высокой точностью установлено, что инерциальной является гелиоцентрическая система отсчета. (Гелиоцентрической называется система отсчета, начало координат которой расположено в центре солнца, а оси координат направлены на соответствующим образом выбранные звезды.) Можно доказать, что если некоторая система отсчета движется относительно инерциальной равномерно и прямолинейно, то она также является инерциальной. Общеизвестно, что все тела препятствуют попыткам изменить состояние их движения, тело изменяет свою скорость движения только в том случае, если к нему приложена некоторая сила. Об этом свойстве тел говорят, что все тела обладают определенной инертностью. Количественной мерой инертности является масса тела. Если материальная точка с массой
(1.1)
Всякое протяженное тело можно представить в виде совокупности
Второй закон Ньютона утверждает, что скорость изменения импульса тела равна действующей на тело силе:
Уравнение (1.3) называется уравнением движения тела. Учитывая важность этого уравнения, его часто называют также основным уравнением динамики. Известно, что в школьном курсе физике второй закон Ньютона формулируется несколько иначе – ускорение тела пропорционально приложенной силе и обратно пропорционально его массе:
Возникает вопрос – какая из формулировок правильней? Обе справедливы! Но более общей является формулировка, выражаемая формулой (1.3). Действительно, подставим в уравнение (1.3) выражение для импульса (1.1):
В частном случае, когда масса тела считается постоянной,
т.е. соотношение абсолютно эквивалентное формуле (1.4). Поэтому будем считать, что второму закону Ньютона соответствует уравнение (1.3). Правда в большинстве практических случаев масса тел может считаться постоянной, и с полным правом можно использовать традиционную формулировку – (1.4) или (1.6). Третий закон Ньютона утверждает, что всякое действие одного тела на другое имеет характер взаимодействия и силы, с которыми действуют друг на друга взаимодействующие тела равны по величине и противоположны по направлению:
Как и большинство законов физики, этот закон имеет ограниченную область применения: третий закон всегда выполняется при контактных взаимодействиях тел, а также при взаимодействии на расстоянии покоящихся тел. Если взаимодействующие на расстоянии тела движутся друг относительно друга, то третий закон может нарушаться. Такое, в частности, возможно при взаимодействии заряженных тел. ВИДЫ СИЛ В МЕХАНИКЕ Изучить самостоятельно: 2.4.1. Фундаментальные взаимодействия 2.4.2. Закон всемирного тяготения, гравитационная постоянная. 2.4.3. Природа сил упругости и сил трения. 2.4.4. Упругие силы, относительная деформация, механическое напряжение, закон Гука. 2.4.5. Внутреннее и внешнее трение. Вязкое трение, трение скольжения и качения. 2.4.6. Сила трения покоя. Коэффициент трения. 2.4.7. Зависимость силы трения скольжения от относительной скорости движения трущихся тел. 2.4.8. Сила тяготения, сила тяжести и вес тела. Вес тела в неинерциальных системах отсчета.
При деформации тела возникают силы упругости. Деформацию называют упругой, если после прекращения действия внешних сил тело восстанавливает свою форму. Остановимся на деформациях вида растяжение–сжатие. Допустим, что под действием силы
И он будет находиться под механическим напряжением
Если деформации упругие (!), то выполняется закон ГУКА, согласно которому деформация стержня пропорциональна приложенной силе (для пружин коэффициент пропорциональности часто называют жесткостью):
Другая формулировка закона Гука утверждает, что
где коэффициент пропорциональности
Лекция № 3 ЗАКОНЫ СОХРАНЕНИЯ СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ Силы, действующие на тела рассматриваемой механической системы можно естественным образом разделить на внутренние и внешние. Внутренними будем называть силы, действующие между телами, принадлежащими рассматриваемой системе, внешними – возникающие при взаимодействии тел системы с телами, не принадлежащими системе. Система называется замкнутой, если внешние силы отсутствуют. Для замкнутых систем существуют такие. Из множества интегралов движения интерес представляют только аддитивные. Таких интегралов существует только три, и ими являются энергия, импульс и момент импульса. Соответственно существуют три закона сохранения, которые связаны со свойствами пространства и времени. Сохранение энергии связано с однородностью времени, т.е. равнозначностью всех моментов времени. Сохранение импульса связано с однородностью пространства. Сохранение момента импульса – с изотропностью пространства, т.е. одинаковостью его свойств по всем направлениям. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ Попытаемся ответить на вопрос: почему кинетическая энергия частицы выражается формулой С этой целью рассмотрим простейшую систему, состоящую из одной частицы. Уравнение движения частицы имеет вид
Под Умножим (1) на
Теперь учтем, что
Следовательно:
Допустим, что на частицу не действуют внешние силы – . (3.5) Это означает, что для изолированной частицы Т является интегралом движения, и который и называют кинетической энергией частицы. РАБОТА И МОЩНОСТЬ Механической работой силы
Подчеркнем, что эта величина является алгебраической и, если угол Необходимо отметить отличие бытового понимания слова «работа» и понятия «механическая работа». Обратите внимание на то, что человек, переместивший горизонтально предмет в руке, механической работы не совершил, хотя с его точки зрения «свою работу выполнил». Для вычисления работы на произвольном пути S необходимо сложить работы на элементарных перемещениях, т.е. найти интеграл
Возвращаясь к рассматривавшейся нами частице, отметим, что если результирующая сил, действующих на частицу не равна нулю, то кинетическая энергия за все время
Если частица перемещается из точки 1 в точку 2 вдоль некоторой траектории, то, интегрируя соотношение (3.8) вдоль этой траектории, мы получаем:
Левая часть (3.9) представляет собой разность кинетических энергий в точках 1 и 2, а правая – работу результирующей силы:
Таким образом, приходим к выводу: работа результирующей силы идет на приращение кинетической энергии. Отметим, что элементарное перемещение
Часто представляет интерес скорость совершения работы. Эту величину называют мощностью:
Единицей измерения мощности является ватт: 1 Вт = 1 Дж/с. ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Как мы установили ранее (см. соотношение (3.10)), работа результирующей силы, действующей на частицу, идет на приращение ее кинетической энергии. Если на частицу действуют только консервативные силы, то их работа равна по формуле (3.22) равна убыли потенциальной энергии (
Перегруппируем члены в соотношении (3.24) по индексам следующим образом:
Формула (3.25) означает, что в отсутствие неконсервативных сил величина
не изменяется при движении частицы, а значит, является интегралом движения. Эту величину называют полной механической энергией частицы. Если рассматриваемая система состоит из N невзаимодействующих частиц, находящихся в поле консервативных сил, то полная энергия системы
Тогда
Однако полная энергия сохраняется не всегда. Рассмотрим ситуацию, когда на частицу кром
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1051; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.012 с.) |

 , задающего направление вектора
, задающего направление вектора  . Единичный вектор по определению имеет постоянный модуль, а значит изменяться может только по направлению.
. Единичный вектор по определению имеет постоянный модуль, а значит изменяться может только по направлению. Допустим, что за очень малый промежуток времени
Допустим, что за очень малый промежуток времени  вектор
вектор  , а вместе с ним и орт
, а вместе с ним и орт  поворачивается на угол
поворачивается на угол  . В результате
. В результате  =
= 
 , направление которого задается ортом этого приращения
, направление которого задается ортом этого приращения  .
. . (1.1)
. (1.1) при малых
при малых 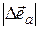 на орт приращения
на орт приращения  , можем записать (а так можно представить любой вектор!):
, можем записать (а так можно представить любой вектор!): (1.2)
(1.2) орт
орт 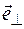 перпендикуляра к вектору
перпендикуляра к вектору  ). Тогда производная по времени орта
). Тогда производная по времени орта  . (1.3)
. (1.3) представляет собой угловую скорость вращения вектора
представляет собой угловую скорость вращения вектора  Траекторией материальной точки будем называть воображаемую линию, вдоль которой движется частица. (Очевидно, что траектория – это, как и сама материальная точка, воображаемый объект, модель.)
Траекторией материальной точки будем называть воображаемую линию, вдоль которой движется частица. (Очевидно, что траектория – это, как и сама материальная точка, воображаемый объект, модель.) .
. за промежуток времени
за промежуток времени  , на величину этого промежутка. Такой расчет дает, очевидно, приближенное значение скорости, а о направлении скорости вообще ничего не позволяет сказать.
, на величину этого промежутка. Такой расчет дает, очевидно, приближенное значение скорости, а о направлении скорости вообще ничего не позволяет сказать.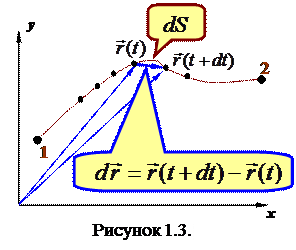 Чтобы дать более строгое определение скорости поступим следующим образом: разобьем мысленно траекторию на участки
Чтобы дать более строгое определение скорости поступим следующим образом: разобьем мысленно траекторию на участки  , которые частица проходит за бесконечно малые промежутки времени
, которые частица проходит за бесконечно малые промежутки времени  (рисунок 1.3.). Каждому участку
(рисунок 1.3.). Каждому участку 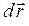 за соответствующий
за соответствующий  . Для бесконечно малого
. Для бесконечно малого  , (1.4)
, (1.4) , направленных в сторону перемещения частицы и совпадающих с
, направленных в сторону перемещения частицы и совпадающих с  дает векторную характеристику быстроты движения точки, модуль которой совпадает с традиционным представлением о скорости.
дает векторную характеристику быстроты движения точки, модуль которой совпадает с традиционным представлением о скорости. (1.5)
(1.5) совпадает с ортом касательной к траектории в данной точке, направленным в сторону движения частицы. Орт касательной к траектории принято обозначать
совпадает с ортом касательной к траектории в данной точке, направленным в сторону движения частицы. Орт касательной к траектории принято обозначать  . Поэтому для вектора скорости в данной точке траектории справедливо соотношение:
. Поэтому для вектора скорости в данной точке траектории справедливо соотношение: (т.е.
(т.е.  ) (1.6)
) (1.6) , для вектора скорости можно записать представление через его проекции на оси координат
, для вектора скорости можно записать представление через его проекции на оси координат  :
: , (1.7)
, (1.7) (1.8)
(1.8)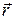 может изменяться по модулю и по направлению. Следует предположить, что вектор скорости всегда можно представить в виде суммы двух векторов, один из которых характеризует изменение
может изменяться по модулю и по направлению. Следует предположить, что вектор скорости всегда можно представить в виде суммы двух векторов, один из которых характеризует изменение  . (1.9)
. (1.9) =
=  , (1.10)
, (1.10) направлена вдоль радиус вектора, а значит характерзует быстроту его изменения по мудулю. Направление второй составляющей,
направлена вдоль радиус вектора, а значит характерзует быстроту его изменения по мудулю. Направление второй составляющей,  , определяется производной орта радиус-вектора:
, определяется производной орта радиус-вектора:  . Как мы уже установили, производная орта определяется выражением (1.3)
. Как мы уже установили, производная орта определяется выражением (1.3) . (1.11)
. (1.11) – угловая скорость поворота радиус-вектора, а
– угловая скорость поворота радиус-вектора, а  - перпендикулярный к нему орт, направленный в сторону поворота. Следовательно, составляющая
- перпендикулярный к нему орт, направленный в сторону поворота. Следовательно, составляющая  перпендикулярна радиус-вектору и характеризует быстроту его изменения по направлению. Модуль скорости связан с составляющими вектора скорости соотношенем:
перпендикулярна радиус-вектору и характеризует быстроту его изменения по направлению. Модуль скорости связан с составляющими вектора скорости соотношенем: . (1.12)
. (1.12) и путь, пройденный ею путь
и путь, пройденный ею путь  от некоторой исходной точки. Если производная по времени от радиус-вектора дает по определению скорость частицы, то какой смысл имеет производная пути по времени?! Чтобы ответить на этот вопрос необходимо вспомнить о том, что модуль приращения радиус-вектора совпадает с элементом траектории
от некоторой исходной точки. Если производная по времени от радиус-вектора дает по определению скорость частицы, то какой смысл имеет производная пути по времени?! Чтобы ответить на этот вопрос необходимо вспомнить о том, что модуль приращения радиус-вектора совпадает с элементом траектории  . Тогда модуль соотношения, определяющего скорость,
. Тогда модуль соотношения, определяющего скорость, . (1.13)
. (1.13) , (1.14)
, (1.14) до
до  , если известна зависимость модуля вектора скорости от времени
, если известна зависимость модуля вектора скорости от времени  .
. Допустим, что зависимость
Допустим, что зависимость  , чтобы можно было считать скорость
, чтобы можно было считать скорость  на отрезке
на отрезке  за каждый интервал
за каждый интервал 
 , а весь путь:
, а весь путь: .м м (1.15)
.м м (1.15) и основанием
и основанием 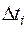 . Сумма (1.15) дает приблизительную площадь фигуры, ограниченной осью времени, графиком
. Сумма (1.15) дает приблизительную площадь фигуры, ограниченной осью времени, графиком  , а
, а  :
: . (1.16)
. (1.16) (1.17)
(1.17) , то, поскольку в соответствии с определением
, то, поскольку в соответствии с определением  есть перемещение за
есть перемещение за 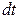 , интеграл
, интеграл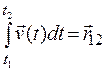 (1.18)
(1.18) . (1.19)
. (1.19)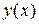 на промежутке изменеия аргумениа от
на промежутке изменеия аргумениа от  до
до  :
: . (1.20)
. (1.20) . (1.21)
. (1.21) (1.22)
(1.22) (1.6), то, по аналогии двумя составляющими вектора скорости, характеризующими изменение радиус-вектора частицы, логично выделить две составляющих ускорения:
(1.6), то, по аналогии двумя составляющими вектора скорости, характеризующими изменение радиус-вектора частицы, логично выделить две составляющих ускорения: . (1.23)
. (1.23) совпадает с
совпадает с  , т.е с касательной к траектории движения и скоростью, поэтому ее называют тангенциальным ускорением. Эта составляющая ускорения определяет быстроту изменения вектора скорости по модулю.
, т.е с касательной к траектории движения и скоростью, поэтому ее называют тангенциальным ускорением. Эта составляющая ускорения определяет быстроту изменения вектора скорости по модулю. направлена перпендикулярно скорости (
направлена перпендикулярно скорости ( – производная орта) и называется нормальным ускорением.
– производная орта) и называется нормальным ускорением.  характеризует быстроту изменения скорости по направлению.
характеризует быстроту изменения скорости по направлению. (см.рис.1.5) касательная к траектории (а значит и вектор скорости) поворачивается на угол
(см.рис.1.5) касательная к траектории (а значит и вектор скорости) поворачивается на угол 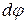 , то кривизной траектории в данной ее точке называется:
, то кривизной траектории в данной ее точке называется:
 . (1.24)
. (1.24) (1.26)
(1.26) - орт нормали к траектории, направленный в сторону поворота касательной к траектории
- орт нормали к траектории, направленный в сторону поворота касательной к траектории  .
. . (1.27)
. (1.27) . (1.28)
. (1.28) . (1.29)
. (1.29)
 . (1.30)
. (1.30) . (1.31)
. (1.31)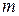 движется со скоростью
движется со скоростью  , то по определению она обладает импульсом
, то по определению она обладает импульсом
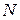 материальных точек с массами
материальных точек с массами 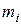 , движущимися со скоростями
, движущимися со скоростями  . Импульсом такого тела называется величина
. Импульсом такого тела называется величина (1.2)
(1.2) (1.3)
(1.3) . (1.4)
. (1.4) (1.5)
(1.5) , в уравнении (1.5) масса выходит из под знака производной и получаем:
, в уравнении (1.5) масса выходит из под знака производной и получаем: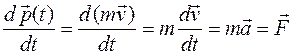 , (1.6)
, (1.6) , (1.7)
, (1.7) 2.4.1. Упругие силы, относительная деформация, механическое напряжение, закон Гука.
2.4.1. Упругие силы, относительная деформация, механическое напряжение, закон Гука. закрепленный слева стержень (рисунок 2.2) с первоначальной длиной
закрепленный слева стержень (рисунок 2.2) с первоначальной длиной  и площадью сечения
и площадью сечения  получает удлинение (абсолютную деформацию)
получает удлинение (абсолютную деформацию)  , равное изменению координаты его конца. При этом его относительная деформация будет равна:
, равное изменению координаты его конца. При этом его относительная деформация будет равна: , (2.11)
, (2.11) , (2.12)
, (2.12) . (2.13)
. (2.13) , (2.14)
, (2.14) называется МОДУЛЕМ ЮНГА.
называется МОДУЛЕМ ЮНГА. ?
? (3.1)
(3.1) в (3.1) подразумевается результирующая сил, действующих на частницу.
в (3.1) подразумевается результирующая сил, действующих на частницу. :
: (3.2)
(3.2) , а
, а  (3.3)
(3.3) (3.4)
(3.4) , т.е. она представляет собой замкнутую систему
, т.е. она представляет собой замкнутую систему  , и величина
, и величина на перемещении
на перемещении  называют скалярную величину
называют скалярную величину . (3.6)
. (3.6) между
между 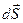 тупой, то сила
тупой, то сила  (3.7)
(3.7) получает приращение:
получает приращение: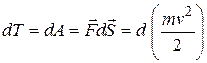 (3.8)
(3.8) (3.9)
(3.9)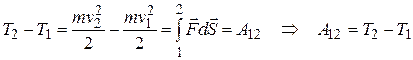 (3.10)
(3.10) можно представить в виде
можно представить в виде  и вычислять работу в промежутке времени от
и вычислять работу в промежутке времени от  по формуле:
по формуле: (3.11)
(3.11) . (3.12)
. (3.12) ) и идет на приращение кинетической энергии частицы:
) и идет на приращение кинетической энергии частицы: . (3.24)
. (3.24)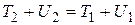 . (3.25)
. (3.25)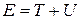 (3.26)
(3.26) также является интегралом движения. Действительно, для каждой частицы справедливо соотношение (3.23), поэтому
также является интегралом движения. Действительно, для каждой частицы справедливо соотношение (3.23), поэтому (3.27)
(3.27) (3.28)
(3.28)


