
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения движения точек механической системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим механическую систему, состоящую из n материальных точек Mi c массами mi (i = 1, 2, …, n), на каждую из которых действует равнодействующая внешних Fi ( e ) и внутренних Fi ( i ) сил. Для каждой точки системы можно записать основное уравнение динамики: mi ai = Fi (e) + Fi (i), (i = 1, 2, …, n). (3.4) Проектируя каждое из уравнений (3.4) на оси координат, получим систему 3 n дифференциальных уравнений второго порядка, описывающих движение системы (3.5)
(i = 1, 2, …, n). О том, насколько сложной является поставленная задача можно судить хотя бы по тому, что к настоящему времени в общем виде она решена только для n = 2. Теорема о движении центра масс. Закон сохранения движения центра масс. Центр масс — воображаемая точка С, положение которой характеризует распределение масс этой системы. Закон движения центра масс — в инерциальных системах отсчёта центр масс системы движется как материальная точка, в которой находится масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. ; Система центра масс — система отсчёта, относительно которой центр масс механической системы неподви жен. Центр масс механической системы движется как точка, масса которой равна массе всей системы M=Σmi, к которой приложены все внешние силы системы:
или в координатной форме:
где
Меры механического движения (количество движения, момент количества движения, кинетическая энергия). Количество движения, мера механического движения, равная для материальной точки произведению её массы m на скорость v. Количество движения Q механической системы равно геометрической сумме Количество движения всех её точек или произведению массы М всей системы на скорость v её центра масс. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ - одна из динамич. характеристик движения материальной точки или механич. системы. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек.
Меры силового воздействия (импульс силы, работа силы). Элементарным импульсом силы называется векторная величина равная произведению силы на бесконечно малый промежуток времени её действия. Импульс силы за конечный промежуток времени равен интегральной сумме:
Работа силы - мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения.
Количество движения. Теорема об изменении количества движения материальной точки. 1)теорема в дифференциальной форме Производная по времени количества движения м.т. равна векторной сумме действующих на неё сил: 2)теорема в конечной (интегральной форме): изменение количества движения м.т. за некоторый промежуток времени, равно векторной сумме импульсов действующих на неё сил: Количество движения, мера механического движения, равная для материальной точки произведению её массы m на скорость v. К. л. mv — величина векторная, направленная так же, как скорость точки. Закон сохранения количества движения м.т.:
2)
Теорема об изменении количества движения механической системы в дифференциальной и интегральной форме. Закон сохранения количества движения.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1074; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.17 (0.01 с.) |

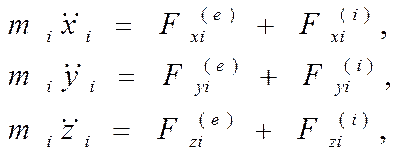
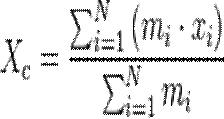
 ;
; 


 - ускорение центра масс и его проекции на оси декартовых координат;
- ускорение центра масс и его проекции на оси декартовых координат;  внешняя сила и ее проекции на оси декартовых координат.
внешняя сила и ее проекции на оси декартовых координат.






 - производная по времени от количества движения мех.сист. равна векторной сумме приложенных к ней внешних сил.
- производная по времени от количества движения мех.сист. равна векторной сумме приложенных к ней внешних сил. - изменение количества движения системы за некоторый промежуток времени равно геометрической сумме импульсов действующих на систему внешних сил за тот-же промежуток времени.
- изменение количества движения системы за некоторый промежуток времени равно геометрической сумме импульсов действующих на систему внешних сил за тот-же промежуток времени.


