
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Масса системы. Центр масс , определение его положения. Положение центра масс при наличии оси или плоскости симметрии. Понятие о центре тяжести.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Масса системы равна алгебраической сумме масс точек или тел её составляющих. Положение центра масс системы определяется радиусом-вектором либо координатами.
Координаты центра масс определяются с помощью этой же формулы относительно (x,y,z)
Центр тяжести- точка пересечения осей, статический момент которой равен нулю. Центр тяжести двух материальных точек имеет весьма простой механический смысл. Представим себе жёсткий “невесомый” стержень АВ, в концах которого помещены массы а и b. “Невесомость” стержня практически означает, что его масса по сравнению с массами a и b настолько незначительна, что ею можно пренебречь. Центр тяжести С материальных точек (A, a) и (B, b) — это такая точка, в которой надо подпереть стержень AB, чтобы он был в равновесии.
Моменты инерции твёрдого тела: полярные и осевые моменты. Зависимость между ними. Радиус инерции. Моментом инерции относительно плоскости называется сумма произведений массы каждой из точек тела на квадрат расстояния от точки до плоскости. Моментом инерции относительно оси наз. Сумма произведений массы каждой из точек системы на квадрат расстояния от точки до оси. Полярный момент инерции (относительно полюса) наз. Сумма произведений массы каждой точки тела на квадрат расстояния от точки до полюса. РАДИУС ИНЕРЦИИ - величина r, имеющая размерность длины, с помощью к-рой момент инерции тела относительно данной оси выражается ф-лой I = Мr, где М - масса тела.
Центробежные моменты инерции. Центробежные моменты для тел, имеющих ось или плоскость симметрии. Центробежный момент инерции относительно двух осей координат называется сумма произведений массы каждой из точек тела на координаты вдоль соответствующих осей.
Если тело имеет ось симметрии, то центробежный момент инерции тела равен нулю и оси у, х являются главными
17. Теорема Гюйгенса-Штейнера о вычислении моментов относительно параллельных осей . Момент инерции твёрдого тела относительно оси не проходящей через центр масс равен сумме моментов инерции относительно центральной оси проходящей через центр масс и параллельной заданной и произведение массы тела на квадрат расстояния между осями.
где JC — известный момент инерции относительно оси, проходящей через центр масс тела, J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями. Вычисление моментов инерции однородных тел: тонкая пластина, тонкий стержень, кольцо, цилиндр, конус. Тонкий стержень: Тонкая пластина: Тонкое кольцо:
Вычисление моментов инерции относительно произвольных осей.
Эллипсоид инерции. Центральные оси инерции. Экстремальные свойства моментов инерции. Центр эллипсоида находится в начале координат. 3 оси симметрии эллипсоида называются главными осями инерции, моменты инерции относительно главных осей называются главными моментами инерции. Если в качестве осей координат принять главные оси инерции, то центробежные моменты инерции относительно этих осей будут равны нулю. ЭЛЛИПСОИД ИНЕРЦИИ -поверхность, характеризующая распределение моментов инерции тела относительно пучка осей, проходящих через фиксированную точку О. Строится Э. и. как геом. место концов отрезков OK= 1/
где Ix, Iy, Iz - осевые, а Ixу, Iyz, Lzx - центробежные моменты инерции тела относительно указанных координатных осей. В свою очередь, зная Э. и. для точки О, можно найти момент инерции относительно любой оси Оl, проходящей через эту точку, из равенства Il= 1/R2, измерив в соот-ветдтвующих единицах расстояние R = OK.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.48.138 (0.009 с.) |

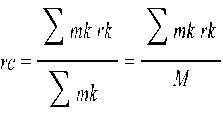 , где rk – радиус-вектор k-той точки или системы
, где rk – радиус-вектор k-той точки или системы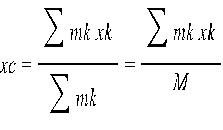
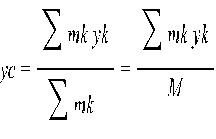
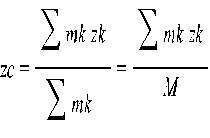



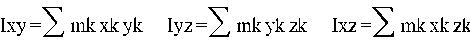
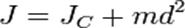
 Тонкий цилиндр:
Тонкий цилиндр: 
 Конус:
Конус: 
 Шар:
Шар: 
 Позволяет найти момент инерции относительно любой оси проходящей через оси координат и составляющие угля
Позволяет найти момент инерции относительно любой оси проходящей через оси координат и составляющие угля с этими осями, через величины осевых и центробежных моментов инерции этих осей.
с этими осями, через величины осевых и центробежных моментов инерции этих осей. , отложенных вдоль Ol от точки О, где Ol- любая ось, проходящая через точку О; Il - момент инерции тела относительно этой оси (рис.). Центр Э. и. совпадает с точкой О, а его ур-ние в произвольно проведённых координатных осях Oxyz имеет вид
, отложенных вдоль Ol от точки О, где Ol- любая ось, проходящая через точку О; Il - момент инерции тела относительно этой оси (рис.). Центр Э. и. совпадает с точкой О, а его ур-ние в произвольно проведённых координатных осях Oxyz имеет вид




