Дифференциальное уравнение вращения тела вокруг неподвижной оси. Колебания физического маятника.

I_zφ”=∑M_z(F_k^e) – ДУ поступательного движения твердого тела.

Φ”=ε – угловое ускорение.

Физический маятник- твердое тело имеющее неподвижную горизонтальную ось вращения не проходящую через центр тяжести и совершающее колебательные движения в горизонтальной плоскости под действием силы тяжести. Ось крепления физ маятника наз ось привеса.

+ *sinφ=0 - ДУ движения физического маятника.

L_пр= приведенная длина физ маятника.

К= - частота

Т=2π - период

 

44. Экспериментальные методы определения моментов инерции.

1) способ качений – используются для тел неправильной формы имеющих отверстия.

Тело подвешивают, определяют его положение центра тяжести, отклоняют из равновесного состояния и приводят в колебательное движение. Экспериментально определяют время τ, n – колебаний и Период Т=τ/n и находят Iz

2)Метод крутильных колебаний

Тело, момент инерции которого необходимо определить, подвешивается на упругом стержне, поворачивается на некоторый угол и отпускается. Начинаются крутильные колебания. Угол закручивания стержня связан с моментом следующим соотношением

= φ K= -частота крутильных колебаний Т=2пи/к

class=WordSection2>

3. способ падающего груза

Метод падающего груза. Недостатком описанных выше двух методов

определения момента инерции ротора является необходимость разборки

двигателя. Метод падающего груза позволяет определить момент инерции

без разборки.

На конце вала или шкива на валу навивают несколько витков гибкого

шнура. Другому концу шнура с прикрепленным к нему грузом дают воз-

можность опускаться (рис. 1.4). При эксперименте измеряют время t, за

которое груз опускается на высоту h. Момент инерции

где m – масса груза, кг;

r – радиус вала или шкива, м;

t –время опускания груза, с;

h – высота опускания груза, м.

Дифференциальные уравнения плоского движения твердого тела.

Плоское движение можно рассматривать как сумму двух движений:

поступательного вместе с центром масс.

Вращательного вокруг оси проходящей через центр масс.

M =∑F_kx^e

M =∑F_ky^e

M =∑F_kz^e ДУ плоского движения.

 

Динамика сферического движения. Динамические уравнения Эйлера.

При сферическом движении рассматривается три независимых вращения:

1 – движение вокруг подвижной оси О_z с угловой скоростью собственного движения ω_φ

2 – вращение вокруг неподвижной оси О_z1 с угловой скоростью прицесии ω_ψ

3 - вращение вокруг вокруг линии узлов с угловой скоростью нутации ω_θ.

=M_x^e I_x +ω_y ω_z(I_z-I_y)=M_x^e

=M_y^e I_y +ω_z ω_x(I_x-I_z)=M_y^e

=M_z^e I_z +ω_x ω_y(I_y-I_x)=M_z^e ДУ Эйлера.

 

 

Приближенная теории гироскопов. Гироскоп с двумя, тремя степенями свободы. Гироскопический эффект, гироскопический момент.

Гироскоп – твёрдое тело, имеющее одну неподвижную точку и совершающее движение вокруг этой точки с большой угловой скоростью. Если центр тяжести гироскопа совпадает с неподвижной точкой, гироскоп называется астатическим. В любом другом случае - тяжёлым. В общем случае гироскоп имеет три степени свободы. Если угол нутации не меняется, то гироскоп имеет две степени свободы. Гироскоп с двумя степенями свободы участвует одновременно в двух движениях: в собственном вращении с угловой скоростью; и прецессионном. При расчётах с использованием приближённой теории используется теорема Резаля.

U= =M₀^e

У гироскопа с тремя степенями свободы все три угла Эйлера изменяются в процессе движения. Поэтому его движение ограничивается только одной неподвижной точкой О.

М₀ вызывает действие на опоры в точках А и В дополнительного момента М_r= - М₀^r – гироскопического момента. Наличие гироскопического момента называется гироскопическим эффектом.

Принцип Даламбера для механической системы. Принцип Даламбера для материальной точки. Примеры.

При движении механической системы главный вектор и главный момент внешних сил относительно произвольного центра как бы устанавливается главным вектором и главным моментом относительно того же центра сил инерции.

∑F_k^e+R^u=0

∑M₀(F_k^e)+M₀^u=0

Принцип Даламбера устанавливает единый подход к исследованию движения любой механической системы вне зависимости от характера налагаемых на это движение условий. При этом динамическим дифференциальным уравнениям движения придается вид уравнений равновесия. Рассмотрим несвободную материальную точку М, движущуюся по кривой АВ под действием активных сил, равнодействующая которых равна F. Обозначив через N силу реакции, с которой кривая АВ действует на точку М, запишем основное уравнение динамики точки/ Силы F, N, Ф образуют сходящуюся систему сил и полученное уравнение выражает условие равновесия этой системы, что и составляет принцип Даламбера для материальной точки.
В каждый момент движения материальной точки действующие на нее активные силы, силы реакций наложенных на точку связей и условно приложенная к точке сила инерции образуют уравновешенную систему сил.
Прикладывая силу инерции к движущейся точке, мы можем говорить лишь об условном равновесии приложенных к ней сил. Однако такая трактовка динамического уравнения движения в некоторых случаях обеспечивает наиболее простое и удобное решение задач динамики - (особенно первой), и поэтому принцип Даламбера широко применяется во многих прикладных дисциплинах.

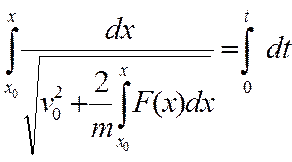При движении материальной точки векторная сумма действующих на ней активных сил, равнодействующих реакций и сила инерции будет равна нулю.

Сила инерции равна произведению массы тела на его ускорение и направлена противоположно ускорению. Ф=-ma