
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передачи с неподвижными осями колёсСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основная задача кинематического анализа любых зубчатых передач состоит в определении передаточного отношения. Как и в плоском зацеплении, в любой передаче, состоящей из двух вращающихся звеньев, передаточное отношение от первого звена ко второму
Согласно формуле, общее передаточное отношение равно произведению всех промежуточных. Индексы при Пример. В передаче, изображённой на рис. 5.23, известны числа зубьев
Рис. 5.23. Зубчатая передача с неподвижными осями колёс Решение. Рассмотренная передача называется ступенчатой. Колёса 1, 2а образуют первую ступень; 3а, 2б – вторую; 4, 3б – третью. Если все колёса лежат в одной плоскости или, говоря иначе, расположены в один ряд, то передача называется р
Рис. 5.24. Р Для этой передачи Для передач с параллельными осями – рядовых и ступенчатых – имеет смысл знак передаточного отношения. Он положительный, если колёса вращаются в одном направлении, и отрицательный, если в разных. Знак общего передаточного отношения можно установить алгебраически через знаки промежуточных передаточных отношений или визуально, обходя колёса по маршруту, показанному на рис. 5.24 волнистой стрелкой. Стрелка показывает, что крайние колёса вращаются в разных направлениях, и значит, общее передаточное отношение – Планетарные передачи Передача называется планетарной, если она содержит хотя бы одно колесо с подвижной осью (рис. 5.25, а, б). Колесо с подвижной осью называется сателлитом. В данном примере – это колесо 2. Звено Сателлитов может быть несколько, это увеличивает нагрузочную способность передачи, однако для кинематического анализа достаточно принять во внимание только один сателлит. Колёса представлены на схеме своими центроидами или, иначе, начальными окружностями. Числа зубьев Основная задача анализа состоит в определении передаточного отношения Картина линейных скоростей представляет собой совокупность линий распределения скоростей всех точек, лежащих на оси, проходящей вдоль водила. Для построения картины схему изображают в произвольном масштабе, при этом радиусы начальных окружностей определяют исходя из пропорциональности этих радиусов числам зубьев. Обозначают шарниры
Рис. 5.25. Планетарная передача – а, б и картина угловых скоростей – в Скорость точки Скорость на подвижном конце водила такая же, как в центре сателлита. Водило вращается вокруг точки Картина угловых скоростей. Если все линейные скорости отнести к одному и тому же расстоянию Из точки Для определения передаточного отношения масштаб картины не имеет значения, поэтому достаточно измерить длины отрезков Аналитическое определение величины
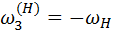 ; колесо 1 имеет скорость ; колесо 1 имеет скорость 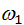 относительно корпуса и относительно корпуса и 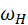 вместе с корпусом; результирующая скорость вместе с корпусом; результирующая скорость 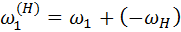 . Передаточное отношение от звена 1 к 3 . Передаточное отношение от звена 1 к 3
Обращённый механизм равносилен переставленному на водило. На этом основании Теперь задача сводится к выражению величины
5.7.3 Синтез планетарной передачи Синтез состоит в подборе чисел зубьев. Основным условием синтеза является обеспечение заданного передаточного отношения Условие соосности состоит в том, чтобы оси центральных звеньев лежали на одной прямой. Условие сборки или, иначе, собираемости передачи состоит в том, чтобы напротив зуба одного колеса находилась впадина другого. При одном сателлите это условие выполняется всегда, при нескольких сателлитах числа зубьев надо подбирать специально. Условие соседства сателлитов состоит в том, чтобы соседние сателлиты не задевали друг друга. Такое возможно, начиная с трёх сателлитов. Основное условие синтеза выражает формула (5.12). Условие соосности удовлетворяется, если радиусы начальных окружностей связаны уравнением
Условие сборки. Сателлиты делят передачу на несколько одинаковых секторов, количество которых равно числу сателлитов
Последнее слагаемое есть целое число, равное
Если задаться числами
Рис. 5.27. К выводу условия сборки Вместо чисел Пример. Решение. Подставляя
Пусть Пропущенное нами условие соседства сателлитов легко проверяется графически. Если условие не выполняется, то задаются другим числом сателлитов и повторяют расчёт. Волновая передача Передача состоит из волнообразователя Обычно задача анализа состоит в определении передаточного отношения Рис. 5.28. Волновая передача Согласно методу, корпусу механизма – звену 3 – сообщают скорость
Силовой расчёт механизмов Постановка задачи В данном курсе силовой расчёт или, иначе, силовой анализ рассматривается только для плоских механизмов. Предполагается, что высшие пары заменены низшими и, следовательно, механизм приведён к рычажному виду. Расчёт ведётся по двумерной модели. Как правило, такая модель не содержит избыточных связей и механизм оказывается статически определимым. Предполагается также, что трение пренебрежимо мало. Расчёт состоит в определении реакций связей в кинематических парах механизма по заданному положению и движению (скорости и ускорению) одного из звеньев этого механизма. При заданном движении величину одной из внешних сил не задают. Её определяют исходя из того, чтобы она в совокупности с другими внешними силами обеспечивала заданное движение. Для краткости незаданную внешнюю силу называют уравновешивающей. Она действительно является таковой по отношению к внешним силам и силам инерции. Реакции связей существенно зависят от сил инерции. В свою очередь силы инерции зависят от ускорений, поэтому силовому расчёту предшествует кинематический анализ. Конечной целью этого анализа является определение ускорений центров масс и угловых ускорений звеньев. Ниже предполагается, что ускорения определены. Силы инерции Силы инерции каждого звена представляют сначала в виде главного вектора
где m – масса звена; Чтобы унифицировать силы, а именно свести их только к векторам, избавляются от главного момента Методы силового расчёта Первый метод – позвенный, состоит в том, что механизм разбивают на отдельные звенья. К каждому звену прикладывают три категории сил: внешние (для механизма) силы, реакции связей, силы инерции. Внешние силы делятся на: движущие – Реакции связей представляют двумя взаимно перпендикулярными составляющими
Рис. 6.1. Силы, действующие на звенья механизма: На рис. 6.1, в показаны все три категории сил, приложенных к звену 5. Неизвестные силы выделены пунктиром. Силы инерции представлены в безмоментной форме. Согласно принципу Даламбера, приложение сил инерции ко всем внешним силам и реакциям связей приводит любое звено в состояние равновесия. Совместно решая систему уравнений равновесия всех звеньев, находят реакции и незаданную внешнюю силу. Совместное решение целесообразно только при машинном решении задачи. Второй метод – погруппный, применяется при ручном графоаналитическом решении задачи. Он состоит в том, что реакции определяют не для всех звеньев сразу, а лишь для отдельных групп этих звеньев. В выделенных группах число реакций должно быть равно числу уравнений равновесия. Число реакций равно числу активных связей s, содержащихся во всех парах группы. Для произвольной системы сил число уравнений равновесия равно 3 п, где п – число звеньев группы. В итоге искомые группы должны удовлетворять условию Такому условию удовлетворяют, как известно, группы Ассура (см. пункт 3.1.1). При разложении на группы Ассура за начальное принимают звено 1 (см. рис. 6.1, а), к которому приложена незаданная внешняя сила Пример погруппного силового расчёта Пусть требуется определить реакции в кинематических парах шестизвенного механизма, показанного на рис. 6.2, а. Схема вычерчена в определённом масштабе. Это значит, что все размеры доступны. Известны массы и моменты инерции звеньев. Задана скорость кривошипа 1. Эта скорость постоянна. Известна сила полезного сопротивления Предполагается, что кинематический анализ уже произведён и определены главные векторы Звено 1 принято за начальное, т. к. к нему приложен незаданный момент Рассчитываемую группу отделяют от механизма и изображают отдельно (рис. 6.2, б). Положение звеньев группы не изменяют. Масштаб группы произвольный. К группе прикладывают внешние силы Рис. 6.2. Силовой расчёт механизма Расчёт группы 4, 5 Линию действия реакции Связи стойки 0 с ползуном 5 можно считать расположенными в его опорах – по одной связи на каждую опору. Реакции этих связей представляют в виде равнодействующей При графоаналитическом силовом расчёте уравнения равновесия записывают в виде суммы моментов Рассматриваемая группа имеет три внешних неизвестных –
Неизвестные выделены чертой снизу. Графическое решение уравнения геометрической суммы называется планом сил. План сил строится в определенном масштабе. Масштабный коэффициент Построив цепь из первых трёх сил, через конец вектора Направления искомых сил удобно определять по следующему правилу: если геометрическая сумма сил равна нулю, то искомые силы оказываются попутными обходу векторного контура в направлении известных сил. Применяя это правило к построенному плану сил, находят, что направления векторов Направление силы Расстояние
Отсюда: Внутренняя реакция Расчёт группы 2, 3 Внешними силами данной группы являются Реакции в шарнирах В и D представляют в виде двух взаимно перпендикулярных составляющих, направленных вдоль и поперёк соответствующего звена. Продольную составляющую называют нормальной, поперечную – тангенциальной. Силы инерции представляют в безмоментной форме. При этом На начало расчёта имеются четыре неизвестных:
Буквой h с соответствующим индексом обозначены плечи сил. Их значения снимают с чертежа. Чтобы не перегружать рисунок, плечи не показаны. Из уравнения моментов находят реакцию Для сил, действующих на звено 3, уравнение моментов относительно точки С имеет вид
Отсюда находят
С помощью плана сил (рис. 6.2, д) находят реакции
С помощью этого уравнения определяют Расчёт начального механизма Из трёх категорий сил, которые необходимо приложить к звену 1, показывают сначала реакцию
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.016 с.) |

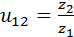 . Для более сложных передач с неподвижными осями общее передаточное отношение, т. е. передаточное отношение от первого звена к последнему -му, определяют по формуле
. Для более сложных передач с неподвижными осями общее передаточное отношение, т. е. передаточное отношение от первого звена к последнему -му, определяют по формуле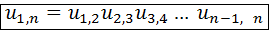 . (5.10)
. (5.10)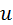 указывают номера звеньев, а не номера зубчатых колёс, которых у звена может быть несколько. Заменяя каждое
указывают номера звеньев, а не номера зубчатых колёс, которых у звена может быть несколько. Заменяя каждое 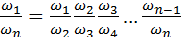 . После сокращений уравнение обращается в тождество, что доказывает справедливость формулы (5.10).
. После сокращений уравнение обращается в тождество, что доказывает справедливость формулы (5.10).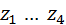 всех колёс. Требуется определить передаточное отношение
всех колёс. Требуется определить передаточное отношение 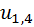 .
.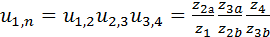 .
. довой, пример приведён на рис. 5.24.
довой, пример приведён на рис. 5.24.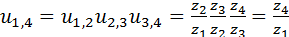 . Результат показывает, что передаточное отношение рядовой передачи зависит от чисел зубьев только крайних колёс.
. Результат показывает, что передаточное отношение рядовой передачи зависит от чисел зубьев только крайних колёс.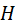 , несущее сателлит, называется водилом. Звенья 1, 3,
, несущее сателлит, называется водилом. Звенья 1, 3, 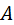 , – главная.
, – главная.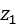 ,
, 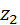 ,
,  всех колёс при анализе считаются известными, поэтому есть возможность изобразить схему в некотором масштабе.
всех колёс при анализе считаются известными, поэтому есть возможность изобразить схему в некотором масштабе.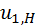 . Это передаточное отношение от центрального колеса к водилу. Задача может быть решена как графически, так и аналитически. Графическое решение опирается на картины линейных и угловых скоростей.
. Это передаточное отношение от центрального колеса к водилу. Задача может быть решена как графически, так и аналитически. Графическое решение опирается на картины линейных и угловых скоростей. и точки касания
и точки касания  ,
,  окружностей всех колёс. Задаются скоростью какой-нибудь из обозначенных точек, например скоростью точки
окружностей всех колёс. Задаются скоростью какой-нибудь из обозначенных точек, например скоростью точки  произвольной длины. Соединив точки
произвольной длины. Соединив точки 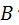 , получают линию распределения скоростей колеса 1.
, получают линию распределения скоростей колеса 1. в центре сателлита.
в центре сателлита.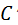 , получают линию распределения скоростей водила. На этом построение картины линейных скоростей завершено.
, получают линию распределения скоростей водила. На этом построение картины линейных скоростей завершено.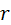 от центра вращения, то на основании известной формулы
от центра вращения, то на основании известной формулы 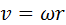 эти линейные скорости можно рассматривать как угловые. В качестве
эти линейные скорости можно рассматривать как угловые. В качестве 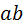 (рис. 5.25, в).
(рис. 5.25, в).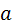 проводят лучи, параллельные линиям распределения скоростей. На прямой, перпендикулярной
проводят лучи, параллельные линиям распределения скоростей. На прямой, перпендикулярной 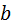 . Например, отрезок
. Например, отрезок 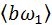 изображает скорость
изображает скорость  ,
, 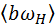 – скорость
– скорость 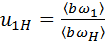 .
. . Отсюда
. Отсюда . (5.11)
. (5.11)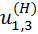 можно называть передаточным отношением механизма, переставленного на водило. С учётом этого замечания выделенная формула читается так: Передаточное отношение от центрального колеса к водилу равно единице минус передаточное отношение от того же центрального колеса к другому центральному после перестановки механизма на водило.
можно называть передаточным отношением механизма, переставленного на водило. С учётом этого замечания выделенная формула читается так: Передаточное отношение от центрального колеса к водилу равно единице минус передаточное отношение от того же центрального колеса к другому центральному после перестановки механизма на водило. . Знак «минус» поставлен потому, что колёса 1 и 3 вращаются во взаимно противоположных направлениях. После подстановки в (5.11) получают:
. Знак «минус» поставлен потому, что колёса 1 и 3 вращаются во взаимно противоположных направлениях. После подстановки в (5.11) получают: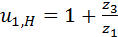 . (5.12)
. (5.12)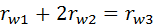 (см. рис. 5.25). Как отмечалось при выводе системы (5.3), радиусы начальных окружностей пропорциональны числам зубьев. С учётом этой пропорциональности условие соосности имеет вид
(см. рис. 5.25). Как отмечалось при выводе системы (5.3), радиусы начальных окружностей пропорциональны числам зубьев. С учётом этой пропорциональности условие соосности имеет вид . (5.13)
. (5.13)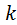 . Один из таких секторов изображён на рис. 5.27. Если обойти зубья по маршруту, выделенному на рисунке жирной линией, то получится цепь, содержащая некоторое целое число зубьев
. Один из таких секторов изображён на рис. 5.27. Если обойти зубья по маршруту, выделенному на рисунке жирной линией, то получится цепь, содержащая некоторое целое число зубьев 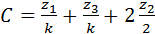 .
. , и условие сборки принимает вид:
, и условие сборки принимает вид: . (5.14)
. (5.14)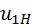 ,
,  и
и 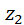 ,
, 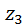 . На этом задачу можно считать решённой. Однако, решив уравнения, можно получить слишком большие или, наоборот, слишком малые числа зубьев. Чтобы этого избежать, условиям синтеза придают форму пропорции:
. На этом задачу можно считать решённой. Однако, решив уравнения, можно получить слишком большие или, наоборот, слишком малые числа зубьев. Чтобы этого избежать, условиям синтеза придают форму пропорции: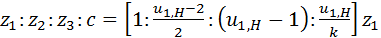 . (5.15)
. (5.15)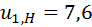 ;
; 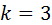 . Требуется определить
. Требуется определить 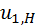 и
и  .
. , тогда скобки будут содержать только целые числа:
, тогда скобки будут содержать только целые числа: 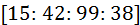 . Из сопоставления с левой частью уравнения находят:
. Из сопоставления с левой частью уравнения находят:  ,
,  ,
,  ,
, 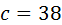 .
. в направлении от волнообразователя к гибкому колесу. Как и в случае планетарных передач, эта задача эффективно решается методом обращения движения.
в направлении от волнообразователя к гибкому колесу. Как и в случае планетарных передач, эта задача эффективно решается методом обращения движения.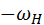 . После этого звено H останавливается, а вал звена 1 обретает скорость
. После этого звено H останавливается, а вал звена 1 обретает скорость  . В обращённом механизме передаточное отношение от звена 1 к звену 3 выражает формула
. В обращённом механизме передаточное отношение от звена 1 к звену 3 выражает формула 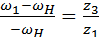 . Отсюда после преобразований получают:
. Отсюда после преобразований получают: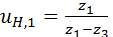 . (5.16)
. (5.16)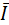 и главного момента
и главного момента  . Их модули определяют по формулам
. Их модули определяют по формулам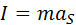 ;
; 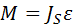 ,
,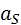 – ускорение центра масс;
– ускорение центра масс; 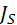 – момент инерции звена относительно центра масс;
– момент инерции звена относительно центра масс; 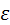 – угловое ускорение звена. Главный вектор прикладывают к центру масс звена и направляют противоположно ускорению
– угловое ускорение звена. Главный вектор прикладывают к центру масс звена и направляют противоположно ускорению  , главный момент изображают круговой стрелкой, направленной противоположно угловому ускорению e.
, главный момент изображают круговой стрелкой, направленной противоположно угловому ускорению e. . При
. При  это делают параллельным смещением вектора
это делают параллельным смещением вектора  . Направление смещения выбирают так, чтобы после смещения вектор
. Направление смещения выбирают так, чтобы после смещения вектор 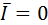 главный момент представляют в виде пары сил
главный момент представляют в виде пары сил 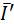 ,
, 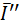 с произвольным плечом
с произвольным плечом 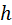 . При этом
. При этом 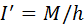 .
.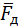 или момента
или момента 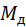 ; силы полезного сопротивления, тоже в виде вектора
; силы полезного сопротивления, тоже в виде вектора  или момента
или момента 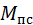 ; силы тяжести –
; силы тяжести –  …
… 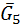 (рис. 6.1, а). Цифровой индекс в обозначении силы тяжести или силы инерции указывает номер звена приложения этой силы.
(рис. 6.1, а). Цифровой индекс в обозначении силы тяжести или силы инерции указывает номер звена приложения этой силы. ,
, 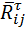 (рис. 6.1, б).
(рис. 6.1, б). .
.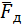 . При этом порядок образования механизма будет следующим: 0, 1 + 2, 3 + 4, 5. Силовой расчёт ведут в обратном порядке, т. е. 4, 5; 2, 3; 0, 1. Такой порядок обусловлен тем, что на начало расчёта условие
. При этом порядок образования механизма будет следующим: 0, 1 + 2, 3 + 4, 5. Силовой расчёт ведут в обратном порядке, т. е. 4, 5; 2, 3; 0, 1. Такой порядок обусловлен тем, что на начало расчёта условие 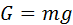 , где g – ускорение свободного падения. Движущий момент
, где g – ускорение свободного падения. Движущий момент  и главные моменты
и главные моменты 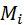 сил инерции всех звеньев. Причём,
сил инерции всех звеньев. Причём, 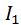 и
и  равны нулю ввиду неподвижности центров масс
равны нулю ввиду неподвижности центров масс 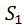 ,
, 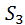 соответствующих звеньев;
соответствующих звеньев; 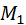 равно нулю, т. к. равно нулю угловое ускорение звена 1;
равно нулю, т. к. равно нулю угловое ускорение звена 1; 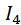 и
и  равны нулю из-за того, что масса и момент инерции звена 4 пренебрежимо малы. Силы инерции, подлежащие учёту, показаны на схеме механизма.
равны нулю из-за того, что масса и момент инерции звена 4 пренебрежимо малы. Силы инерции, подлежащие учёту, показаны на схеме механизма.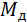 . Первую группу Ассура образуют звенья 2, 3,
. Первую группу Ассура образуют звенья 2, 3, 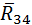 ,
, 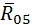 и единственную силу инерции
и единственную силу инерции 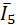 . Масштаб сил на этом этапе расчёта не соблюдают.
. Масштаб сил на этом этапе расчёта не соблюдают.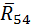 (
(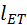 до точки Т определяют наряду с реакциями.
до точки Т определяют наряду с реакциями.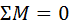 и в виде геометрической суммы сил
и в виде геометрической суммы сил 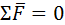 . Сначала определяют внешние реакции, затем внутренние. Уравнение моментов применяют обычно к отдельным звеньям, а уравнение геометрической суммы сил – к группе в целом. Уравнение сил как векторное позволяет найти сразу два неизвестных. Это либо величины двух сил с известными линиями действия, либо величина и направление одной силы.
. Сначала определяют внешние реакции, затем внутренние. Уравнение моментов применяют обычно к отдельным звеньям, а уравнение геометрической суммы сил – к группе в целом. Уравнение сил как векторное позволяет найти сразу два неизвестных. Это либо величины двух сил с известными линиями действия, либо величина и направление одной силы.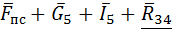 +
+  .
.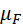 плана определяют, ориентируясь на самую большую из известных сил. Пусть это будет
плана определяют, ориентируясь на самую большую из известных сил. Пусть это будет  ñ, получают:
ñ, получают:  / á F псñ.
/ á F псñ.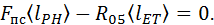
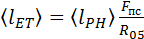 . В данном случае
. В данном случае 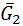 и
и 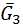 (рис. 6.2, г). Реакция
(рис. 6.2, г). Реакция 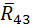 равна и противоположна уже известной
равна и противоположна уже известной 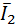 проходит через некоторую точку
проходит через некоторую точку  , а
, а 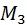 представляют парой
представляют парой 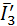 ,
, 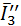 , найденной как
, найденной как  .
.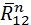 ,
, 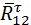 ,
,  ,
, 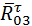 . Сначала определяют тангенциальные составляющие. Для этого используют уравнения моментов относительно точки С. Для сил, действующих на звено 2, уравнение моментов имеет вид
. Сначала определяют тангенциальные составляющие. Для этого используют уравнения моментов относительно точки С. Для сил, действующих на звено 2, уравнение моментов имеет вид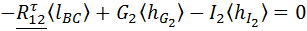 .
.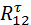 . Если она получится со знаком «минус», то это значит, что истинное направление данной реакции противоположно показанному на рисунке. Чтобы это не забылось, на реакции ставят какую-нибудь метку, например крестик.
. Если она получится со знаком «минус», то это значит, что истинное направление данной реакции противоположно показанному на рисунке. Чтобы это не забылось, на реакции ставят какую-нибудь метку, например крестик.
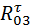 .Нормальные составляющие находят из геометрической суммы сил, действующих на группу в целом. Сначала перечисляют силы, действующие на звено 3, затем на звено 2. Можно и наоборот. Неизвестные оставляют на конец уравнения. Необходимо позаботиться также о том, чтобы нормальные и тангенциальные составляющие реакции одного и того же звена оказались на будущем плане сил рядом. С учётом всех этих рекомендаций получают:
.Нормальные составляющие находят из геометрической суммы сил, действующих на группу в целом. Сначала перечисляют силы, действующие на звено 3, затем на звено 2. Можно и наоборот. Неизвестные оставляют на конец уравнения. Необходимо позаботиться также о том, чтобы нормальные и тангенциальные составляющие реакции одного и того же звена оказались на будущем плане сил рядом. С учётом всех этих рекомендаций получают: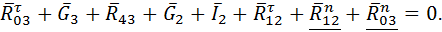
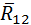 . Равнодействующую не показывают, чтобы не усложнять рисунок. Внутреннюю реакцию
. Равнодействующую не показывают, чтобы не усложнять рисунок. Внутреннюю реакцию 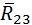 или, наоборот,
или, наоборот,  находят из геометрической суммы сил, действующих соответственно на звено 3 или 2. Останавливаясь на звене 3, получают:
находят из геометрической суммы сил, действующих соответственно на звено 3 или 2. Останавливаясь на звене 3, получают: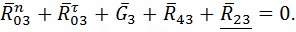
 (рис. 6.2, е). Она равна и противоположна реакции
(рис. 6.2, е). Она равна и противоположна реакции 


