Цилиндрические косозубые передачи
Образование косозубого зацепления
С цилиндра радиуса  на цилиндр радиуса на цилиндр радиуса 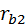 перематывается гибкая нерастяжимая лента (рис. 5.16). перематывается гибкая нерастяжимая лента (рис. 5.16).
| Рис. 5.16. Косозубое зацепление
| С лентой неизменно связана прямая 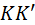 , проведённая под углом , проведённая под углом  к прямой к прямой  , параллельной осям цилиндров. Из теории плоского зацепления известно, что точка , параллельной осям цилиндров. Из теории плоского зацепления известно, что точка 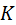 описывает в передней торцевой плоскости эвольвенты Э 1, Э 2 основных окружностей радиусов описывает в передней торцевой плоскости эвольвенты Э 1, Э 2 основных окружностей радиусов  , , 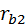 . Такие же эвольвенты описывают другие точки прямой . Такие же эвольвенты описывают другие точки прямой 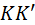 . Совокупность эвольвент образует боковые поверхности зубьев косозубого зацепления. Цилиндры радиусов . Совокупность эвольвент образует боковые поверхности зубьев косозубого зацепления. Цилиндры радиусов  , , 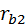 называются основными. При вращении этих цилиндров назад прямая называются основными. При вращении этих цилиндров назад прямая 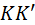 намотается на нижний основной цилиндр и превратится в винтовую линию намотается на нижний основной цилиндр и превратится в винтовую линию  с углом наклона с углом наклона  . .
В любом цилиндрическом сечении, соосном основному цилиндру, эвольвенты располагаются также по винтовой линии, поэтому полученную боковую поверхность косого зуба называют эвольвентной винтовой. Несмотря на двоякую кривизну, поверхности косых зубьев касаются друг другапо прямой, а именно по рисующей прямой 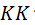 . След прямой . След прямой 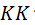 в пространстве стойки называется плоскостью зацепления. Как и линия зацепления в пространстве стойки называется плоскостью зацепления. Как и линия зацепления 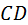 , плоскость зацепления имеет границы – , плоскость зацепления имеет границы –  и и 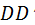 . .
Через полюс зацепления 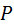 проходят начальные окружности, поэтому цилиндры радиусов проходят начальные окружности, поэтому цилиндры радиусов 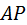 и и 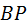 называются начальными. Существуют также делительные цилиндры, в нулевом и равносмещённом зацеплениях они совпадают с начальными цилиндрами. называются начальными. Существуют также делительные цилиндры, в нулевом и равносмещённом зацеплениях они совпадают с начальными цилиндрами.
Изготовление зацепления
Зацепление изготовляют преимущественно методом обката. Обкат происходит по поверхностям A 1, A 2, A 3 (рис. 5.17), образованным от центроид Ц 1, Ц 2, Ц 3, известных по плоскому зацеплению.
Рис. 5.17. Образование косозубого зацепления методом обката
Линия  касания поверхностей обката является мгновенной осью вращения во взаимном движении этих поверхностей, поэтому их называют аксоидами. касания поверхностей обката является мгновенной осью вращения во взаимном движении этих поверхностей, поэтому их называют аксоидами.
Косозубое зацепление образуют тем же производящим контуром 1, что и в случае плоского зацепления. Контур совершает два движения – вместе с аксоидом A 3 и относительно этого аксоида. Второе движение контур совершает перпендикулярно самому себе. В результате второго движения в пространстве 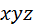 аксоида A 3 создаётся гребенчатый след, называемый производящей поверхностью. Двигаясь с аксоидом A 3, производящая поверхность формирует косозубое зацепление. аксоида A 3 создаётся гребенчатый след, называемый производящей поверхностью. Двигаясь с аксоидом A 3, производящая поверхность формирует косозубое зацепление.
Параметры косозубого колеса. При расчёте этих параметров различают два сечения производящей поверхности. Первое – перпендикулярно граням этой поверхности, второе – перпендикулярно оси колеса. Первое сечение совпадает с производящим контуром 1 и называется нормальным, второе называется торцевым и образует производящий контур 2, отличающийся от контура 1 шагом и углом профиля. Всем величинам, относящимся к нормальному сечению, присваивают индекс n, а относящимся к торцевому сечению – индекс t. Параметры нормального сечения известны по плоскому зацеплению. Найдем параметры торцевого сечения.
В треугольнике 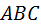 угол при точке угол при точке  – прямой, угол при точке – прямой, угол при точке 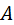 равен равен 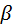 , сторона , сторона 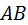 есть шаг есть шаг  в нормальном сечении, в нормальном сечении,
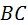 – шаг – шаг  в торцевом сечении. Из треугольника следует: в торцевом сечении. Из треугольника следует:  . Поделив . Поделив  и и  на число на число  , получают так называемый торцевой , получают так называемый торцевой  и нормальный и нормальный  модули. Нормальный модуль – это модуль контура 1. Модули связаны соотношением модули. Нормальный модуль – это модуль контура 1. Модули связаны соотношением
 . .
Угол профиля в торцевом сечении находят по формуле
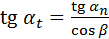 . .
С введением торцевого сечения производящей поверхности задачу определения параметров косозубого колеса в его торцевом сечении решают так же, как плоского колеса. Так, радиусы окружностей, выводимых из станочного зацепления, определяют теперь по формулам:
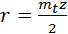 ; ;  ; ;  . .
5.5.3 Коэффициент перекрытия косозубой передачи.
Зубья входят в зацепление в точке 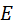 (рис. 5.18), а выходят в точке (рис. 5.18), а выходят в точке  . Фигура . Фигура  называется полем зацепления. За время зацепления точки основной окружности проходят путь, равный отрезку называется полем зацепления. За время зацепления точки основной окружности проходят путь, равный отрезку  . При прочих равных условиях в прямозубом зацеплении этот путь был бы равен отрезку . При прочих равных условиях в прямозубом зацеплении этот путь был бы равен отрезку 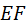 , что заметно меньше. , что заметно меньше.
Коэффициент перекрытия прямозубого и косозубого зацеплений равен отношению отрезков 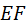 , ,  к шагу соответствующего колеса по нормали к профилям зубьев в их торцевых сечениях. Шаги отличаются не столь значительно, как к шагу соответствующего колеса по нормали к профилям зубьев в их торцевых сечениях. Шаги отличаются не столь значительно, как 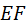 и и  , поэтому в косозубом зацеплении коэффициент перекрытия больше, чем в прямозубом. , поэтому в косозубом зацеплении коэффициент перекрытия больше, чем в прямозубом.
| Рис. 5.18. Поведение контактной линии косых зубьев
|
Контактная линия косых зубьев начинается с точки 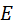 и нарастает постепенно. Нарастание заканчивается в точке и нарастает постепенно. Нарастание заканчивается в точке  . От . От 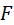 до до  длина линии контакта сокращается до точки. Плавное нарастание и убывание длины контактной линии влечёт за собой плавное изменение нагрузки на зуб. Это, в свою очередь, уменьшает шум при работе передачи. длина линии контакта сокращается до точки. Плавное нарастание и убывание длины контактной линии влечёт за собой плавное изменение нагрузки на зуб. Это, в свою очередь, уменьшает шум при работе передачи.
Конические передачи
Это передачи с пересекающимися осями колёс. Продольные линии зубьев этих зацеплений могут быть как прямолинейными, так и криволинейными. В первом случае зацепление называется прямозубым.
|


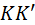 , проведённая под углом
, проведённая под углом  к прямой
к прямой  , параллельной осям цилиндров. Из теории плоского зацепления известно, что точка
, параллельной осям цилиндров. Из теории плоского зацепления известно, что точка 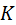 описывает в передней торцевой плоскости эвольвенты Э 1, Э 2 основных окружностей радиусов
описывает в передней торцевой плоскости эвольвенты Э 1, Э 2 основных окружностей радиусов  ,
, 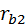 . Такие же эвольвенты описывают другие точки прямой
. Такие же эвольвенты описывают другие точки прямой 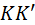 . Совокупность эвольвент образует боковые поверхности зубьев косозубого зацепления. Цилиндры радиусов
. Совокупность эвольвент образует боковые поверхности зубьев косозубого зацепления. Цилиндры радиусов  ,
, 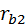 называются основными. При вращении этих цилиндров назад прямая
называются основными. При вращении этих цилиндров назад прямая 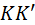 намотается на нижний основной цилиндр и превратится в винтовую линию
намотается на нижний основной цилиндр и превратится в винтовую линию  с углом наклона
с углом наклона  .
.

 на цилиндр радиуса
на цилиндр радиуса 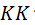 . След прямой
. След прямой 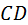 , плоскость зацепления имеет границы –
, плоскость зацепления имеет границы –  и
и 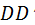 .
.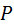 проходят начальные окружности, поэтому цилиндры радиусов
проходят начальные окружности, поэтому цилиндры радиусов 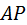 и
и 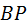 называются начальными. Существуют также делительные цилиндры, в нулевом и равносмещённом зацеплениях они совпадают с начальными цилиндрами.
называются начальными. Существуют также делительные цилиндры, в нулевом и равносмещённом зацеплениях они совпадают с начальными цилиндрами.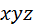 аксоида A 3 создаётся гребенчатый след, называемый производящей поверхностью. Двигаясь с аксоидом A 3, производящая поверхность формирует косозубое зацепление.
аксоида A 3 создаётся гребенчатый след, называемый производящей поверхностью. Двигаясь с аксоидом A 3, производящая поверхность формирует косозубое зацепление.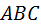 угол при точке
угол при точке  – прямой, угол при точке
– прямой, угол при точке 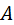 равен
равен 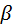 , сторона
, сторона 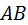 есть шаг
есть шаг  в нормальном сечении,
в нормальном сечении, 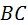 – шаг
– шаг  в торцевом сечении. Из треугольника следует:
в торцевом сечении. Из треугольника следует:  . Поделив
. Поделив  и
и  , получают так называемый торцевой
, получают так называемый торцевой  и нормальный
и нормальный  модули. Нормальный модуль – это модуль контура 1. Модули связаны соотношением
модули. Нормальный модуль – это модуль контура 1. Модули связаны соотношением .
.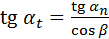 .
.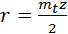 ;
;  ;
;  .
.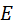 (рис. 5.18), а выходят в точке
(рис. 5.18), а выходят в точке  . Фигура
. Фигура  называется полем зацепления. За время зацепления точки основной окружности проходят путь, равный отрезку
называется полем зацепления. За время зацепления точки основной окружности проходят путь, равный отрезку  . При прочих равных условиях в прямозубом зацеплении этот путь был бы равен отрезку
. При прочих равных условиях в прямозубом зацеплении этот путь был бы равен отрезку 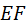 , что заметно меньше.
, что заметно меньше. . От
. От 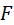 до
до  длина линии контакта сокращается до точки. Плавное нарастание и убывание длины контактной линии влечёт за собой плавное изменение нагрузки на зуб. Это, в свою очередь, уменьшает шум при работе передачи.
длина линии контакта сокращается до точки. Плавное нарастание и убывание длины контактной линии влечёт за собой плавное изменение нагрузки на зуб. Это, в свою очередь, уменьшает шум при работе передачи.


