Группа Ассура с внешней поступательной парой
На рис. 3.9, а эту группу образуют звенья 4, 5. Чтобы не повторяться, движение звеньев 1, 2, 3 предшествующего механизма считается известным. Задача состоит в определении скорости и ускорения только точки 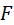 . .
Рис. 3.9. Построение плана скоростей и плана ускорений
для двухзвенной группы Ассура с внешней поступательной парой
Определение скорости точки 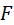 . Для решения задачи вводят систему координат . Для решения задачи вводят систему координат  , движущуюся поступательно, и систему , движущуюся поступательно, и систему  , неизменно связанную со звеном 2 предшествующего механизма. Первую из этих систем считают несущей для звена 4, вторую – несущей для звена 5. Из вытекающих отсюда разложений движения составляют уравнения: , неизменно связанную со звеном 2 предшествующего механизма. Первую из этих систем считают несущей для звена 4, вторую – несущей для звена 5. Из вытекающих отсюда разложений движения составляют уравнения:
 (3.5) (3.5)
До сих пор при составлении уравнений не было необходимости в указании номера звена, к которому относится та или иная точка, т. к. подразумевались шарнирные точки или просто шарниры. Теперь же этого недостаточно, и  – это скорость шарнира – это скорость шарнира 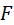 , объединяющего точки , объединяющего точки 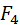 , ,  , а , а  – скорость только точки – скорость только точки  , отмеченной на звене 2 и неизменно связанной с ним. Соответственно, , отмеченной на звене 2 и неизменно связанной с ним. Соответственно,  есть скорость точки есть скорость точки  относительно звена 2. относительно звена 2.
Переносные скорости 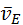 и и  в приведённой выше системе уравнений известны из предполагаемого анализа предшествующего механизма. Относительные скорости известны своими линиями действия, а именно: в приведённой выше системе уравнений известны из предполагаемого анализа предшествующего механизма. Относительные скорости известны своими линиями действия, а именно:  , , 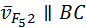 . Всего этого достаточно, чтобы решить систему. Результат показан на рис. 3.9, б. . Всего этого достаточно, чтобы решить систему. Результат показан на рис. 3.9, б.
Определение ускорения точки 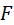 . Из тех же разложений движения, что и в случае скоростей, следует: . Из тех же разложений движения, что и в случае скоростей, следует:
 (3.6) (3.6)
Переносные ускорения  и и  известны из предполагаемого анализа предшествующего механизма. Нормальную составляющую вычисляют по формуле известны из предполагаемого анализа предшествующего механизма. Нормальную составляющую вычисляют по формуле  . Входящую сюда скорость . Входящую сюда скорость  берут из плана скоростей. Тангенциальная составляющая берут из плана скоростей. Тангенциальная составляющая  перпендикулярна перпендикулярна  , величина её неизвестна. , величина её неизвестна.
Ускорение  точки точки  относительно звена 2 параллельно относительно звена 2 параллельно 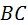 , величина его также неизвестна. Ускорение Кориолиса вычисляют по формуле , величина его также неизвестна. Ускорение Кориолиса вычисляют по формуле  . Входящая сюда скорость . Входящая сюда скорость  предполагается известной из анализа предшествующего механизма. Скорость предполагается известной из анализа предшествующего механизма. Скорость 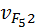 берут из плана скоростей, её изображает вектор берут из плана скоростей, её изображает вектор 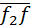 . Направление ускорения Кориолиса получают поворотом вектора . Направление ускорения Кориолиса получают поворотом вектора  на на  ° в сторону скорости ° в сторону скорости  . Таким образом, ускорение . Таким образом, ускорение  известно и по величине, и по направлению. На рисунке его изображает вектор известно и по величине, и по направлению. На рисунке его изображает вектор  . .
Перед решением системы уравнений ускорение  переставляют на последнее место, т. к. оно известно только линией действия. На пересечении линий действия последних слагаемых получают конец f ускорения переставляют на последнее место, т. к. оно известно только линией действия. На пересечении линий действия последних слагаемых получают конец f ускорения  (рис. 3.9, в). (рис. 3.9, в).
Рассмотренный общий случай анализа цепи 4, 5 распадается на два частных. В первом случае (рис.3.10, а) эта цепь приводится
в движение слева, во втором (рис. 3.10, б) – справа. Круговой стрелкой на обеих схемах отмечено звено с заданным движением.
Рис. 3.10. Частные случаи присоединения цепи 4, 5
При определении скоростей в первом случае из системы (3.5) выпадает нижнее уравнение, во втором – верхнее. При определении ускорений в первом случае из системы (3.6) выпадает также нижнее уравнение, во втором – выпадает только ускорение  . Решение упростившихся уравнений не составляет труда, поэтому далее не рассматривается. . Решение упростившихся уравнений не составляет труда, поэтому далее не рассматривается.
Метод кинематических диаграмм
Построение диаграмм
Этот метод применяют, когда интерес представляет положение и движение только выходного звена механизма. Пусть этим звеном является ползун 3 кривошипно-ползунного механизма, изображённого на рис. 3.11, а. Схема механизма вычерчена в масштабе. Положение ползуна характеризует координата 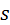 . Её отсчитывают от одного из крайних положений этого звена, обычно – от наиболее удалённого от точки . Её отсчитывают от одного из крайних положений этого звена, обычно – от наиболее удалённого от точки 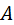 . Именно это и принято на рисунке. В крайнем положении кривошип 1 и шатун 2 вытягиваются в одну прямую . Именно это и принято на рисунке. В крайнем положении кривошип 1 и шатун 2 вытягиваются в одну прямую  . При этом . При этом 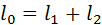 , где , где 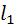 и и 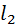 – длины звеньев 1, 2. – длины звеньев 1, 2.
 принимают за начало отсчёта координаты принимают за начало отсчёта координаты 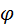 . Этой координате придают ряд равноотстоящих значений в диапазоне от нуля до . Этой координате придают ряд равноотстоящих значений в диапазоне от нуля до  . Для каждого . Для каждого 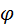 строят схему механизма, отмечая и нумеруя положения точек строят схему механизма, отмечая и нумеруя положения точек  и и  . По положениям точки . По положениям точки  находят координату находят координату 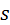 . .
Рис. 3.11. Кинематические диаграммы
кривошипно-ползунного механизма
Каждую пару значений координат 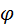 и и 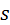 откладывают по заранее заготовленным осям графика откладывают по заранее заготовленным осям графика  (рис. 3.11, б). Масштабные пересчёты делают руководствуясь формулой (3.1). Зависимость координаты выходного звена от координаты входного, в данном случае зависимость (рис. 3.11, б). Масштабные пересчёты делают руководствуясь формулой (3.1). Зависимость координаты выходного звена от координаты входного, в данном случае зависимость  , называют функцией положения механизма. , называют функцией положения механизма.
Двукратным дифференцированием получают графики 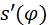 и и  . Принципиально точным является дифференцирование методом касательных. Согласно этому методу в точке дифференцирования, например . Принципиально точным является дифференцирование методом касательных. Согласно этому методу в точке дифференцирования, например 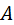 , проводят касательную , проводят касательную  (рис. 3.11, б). (рис. 3.11, б).
Из произвольной точки  , лежащей на оси , лежащей на оси 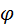 следующего графика, проводят луч, параллельный касательной. Отрезок, отсекаемый лучом на оси следующего графика, проводят луч, параллельный касательной. Отрезок, отсекаемый лучом на оси  , изображает в некотором масштабе производную в точке , изображает в некотором масштабе производную в точке 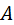 . Продолжая дифференцирование, из той же точки . Продолжая дифференцирование, из той же точки  проводят лучи, параллельные другим касательным к кривой проводят лучи, параллельные другим касательным к кривой  , и получают прочие значения первой производной. , и получают прочие значения первой производной.
При построении графика второй производной касательные проводят к графику первой производной. По завершении построений определяют масштабы, на которых не останавливаемся.
С помощью производных определяют скорость и ускорение ползуна для любого 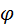 . Скорость . Скорость  есть производная от координаты есть производная от координаты 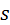 по времени по времени  : :  . Координата . Координата 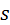 зависит от зависит от 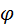 , а , а 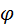 от от  : : 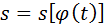 . По правилам дифференцирования сложных функций получают . По правилам дифференцирования сложных функций получают  . Поскольку . Поскольку 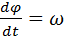 , то скорость ползуна , то скорость ползуна
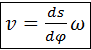 . (3.7) . (3.7)
Ускорение есть производная по времени от скорости. Как показывает формула (3.7), скорость представляет собой произведение двух переменных –  и и  , причём, , причём,  есть известная функция угла есть известная функция угла 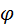 (см. рис. 3.11, б), а (см. рис. 3.11, б), а 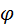 , как и прежде, некоторая функция , как и прежде, некоторая функция  . .
С учётом всего этого  . Производная . Производная  есть ускорение кулачка есть ускорение кулачка 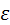 . В итоге, ускорение ползуна . В итоге, ускорение ползуна
 . (3.8) . (3.8)
Используя компактные формы обозначения производных, формулы (3.7), (3.8) представляют в виде:
 ; ; 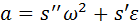 . .
Эти формулы применимы не только к рычажным механизмам, но также к кулачковым и даже зубчатым механизмам. Важно лишь, чтобы движение на входе у них было вращательное, а на выходе поступательное.
|



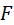 .
. , движущуюся поступательно, и систему
, движущуюся поступательно, и систему  , неизменно связанную со звеном 2 предшествующего механизма. Первую из этих систем считают несущей для звена 4, вторую – несущей для звена 5. Из вытекающих отсюда разложений движения составляют уравнения:
, неизменно связанную со звеном 2 предшествующего механизма. Первую из этих систем считают несущей для звена 4, вторую – несущей для звена 5. Из вытекающих отсюда разложений движения составляют уравнения: (3.5)
(3.5) – это скорость шарнира
– это скорость шарнира 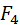 ,
,  , а
, а  – скорость только точки
– скорость только точки  , отмеченной на звене 2 и неизменно связанной с ним. Соответственно,
, отмеченной на звене 2 и неизменно связанной с ним. Соответственно,  есть скорость точки
есть скорость точки 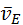 и
и  ,
, 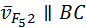 . Всего этого достаточно, чтобы решить систему. Результат показан на рис. 3.9, б.
. Всего этого достаточно, чтобы решить систему. Результат показан на рис. 3.9, б. (3.6)
(3.6) и
и  известны из предполагаемого анализа предшествующего механизма. Нормальную составляющую вычисляют по формуле
известны из предполагаемого анализа предшествующего механизма. Нормальную составляющую вычисляют по формуле  . Входящую сюда скорость
. Входящую сюда скорость  берут из плана скоростей. Тангенциальная составляющая
берут из плана скоростей. Тангенциальная составляющая  перпендикулярна
перпендикулярна  , величина её неизвестна.
, величина её неизвестна. точки
точки 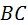 , величина его также неизвестна. Ускорение Кориолиса вычисляют по формуле
, величина его также неизвестна. Ускорение Кориолиса вычисляют по формуле  . Входящая сюда скорость
. Входящая сюда скорость  предполагается известной из анализа предшествующего механизма. Скорость
предполагается известной из анализа предшествующего механизма. Скорость 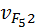 берут из плана скоростей, её изображает вектор
берут из плана скоростей, её изображает вектор 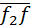 . Направление ускорения Кориолиса получают поворотом вектора
. Направление ускорения Кориолиса получают поворотом вектора  ° в сторону скорости
° в сторону скорости  известно и по величине, и по направлению. На рисунке его изображает вектор
известно и по величине, и по направлению. На рисунке его изображает вектор  .
. (рис. 3.9, в).
(рис. 3.9, в).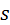 . Её отсчитывают от одного из крайних положений этого звена, обычно – от наиболее удалённого от точки
. Её отсчитывают от одного из крайних положений этого звена, обычно – от наиболее удалённого от точки 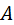 . Именно это и принято на рисунке. В крайнем положении кривошип 1 и шатун 2 вытягиваются в одну прямую
. Именно это и принято на рисунке. В крайнем положении кривошип 1 и шатун 2 вытягиваются в одну прямую  . При этом
. При этом 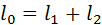 , где
, где 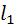 и
и 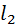 – длины звеньев 1, 2.
– длины звеньев 1, 2. принимают за начало отсчёта координаты
принимают за начало отсчёта координаты 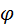 . Этой координате придают ряд равноотстоящих значений в диапазоне от нуля до
. Этой координате придают ряд равноотстоящих значений в диапазоне от нуля до  . Для каждого
. Для каждого  и
и  . По положениям точки
. По положениям точки  (рис. 3.11, б). Масштабные пересчёты делают руководствуясь формулой (3.1). Зависимость координаты выходного звена от координаты входного, в данном случае зависимость
(рис. 3.11, б). Масштабные пересчёты делают руководствуясь формулой (3.1). Зависимость координаты выходного звена от координаты входного, в данном случае зависимость 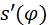 и
и  . Принципиально точным является дифференцирование методом касательных. Согласно этому методу в точке дифференцирования, например
. Принципиально точным является дифференцирование методом касательных. Согласно этому методу в точке дифференцирования, например  (рис. 3.11, б).
(рис. 3.11, б). , лежащей на оси
, лежащей на оси  , изображает в некотором масштабе производную в точке
, изображает в некотором масштабе производную в точке  есть производная от координаты
есть производная от координаты  . Координата
. Координата 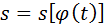 . По правилам дифференцирования сложных функций получают
. По правилам дифференцирования сложных функций получают  . Поскольку
. Поскольку 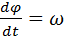 , то скорость ползуна
, то скорость ползуна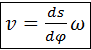 . (3.7)
. (3.7) и
и  , причём,
, причём,  есть известная функция угла
есть известная функция угла  . Производная
. Производная  есть ускорение кулачка
есть ускорение кулачка 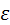 . В итоге, ускорение ползуна
. В итоге, ускорение ползуна . (3.8)
. (3.8) ;
; 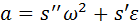 .
.


