Группа Ассура с вращательными парами
Пусть исследуемый механизм имеет схему, показанную на
рис. 3.7, а. Схема вычерчена в определённом масштабе. Для изображённого положения заданы скорость  и ускорение и ускорение 
звена 1. Требуется определить скорости и ускорения всех шарнирных точек, а также угловые скорости и ускорения всех звеньев.
При заданном движении звена 1 первую группу Ассура образует цепь 2, 3, вторую – цепь 4, 5. Это группы с тремя вращательными парами. Анализ начинается с цепи 2, 3. В результате анализа определяют скорости и ускорения точек  , ,  , а также угловые скорости и ускорения звеньев 2, 3. , а также угловые скорости и ускорения звеньев 2, 3.
Рис. 3.7. Построение плана скоростей для двухзвенных
групп Ассура с вращательными парами
Скорости точек  и и  . Скорость точки . Скорость точки  определяют по формуле определяют по формуле  . Всё необходимое для вычисления этой скорости есть. Для определения скорости точки . Всё необходимое для вычисления этой скорости есть. Для определения скорости точки  вводят систему координат вводят систему координат  , движущуюся поступательно. Эту систему принимают за носитель (переносчик) звена 2, т. е. считают, что абсолютное движение звена 2 – движение относительно стойки – состоит из поступательного вместе с системой , движущуюся поступательно. Эту систему принимают за носитель (переносчик) звена 2, т. е. считают, что абсолютное движение звена 2 – движение относительно стойки – состоит из поступательного вместе с системой  и вращательного относительно этой системы. Из такого представления (разложения) движения получают уравнение: и вращательного относительно этой системы. Из такого представления (разложения) движения получают уравнение:
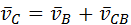 . .
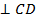  
Под уравнением показана ориентация каждого вектора по отношению к звеньям механизма.
Примечание. Второе слагаемое уравнения читается как скорость точки  относительно относительно  , хотя в действительности это скорость точки , хотя в действительности это скорость точки  относительно системы относительно системы  . Скорость точки . Скорость точки  относительно относительно  равна нулю, т. к. расстояние между этими точками постоянно. равна нулю, т. к. расстояние между этими точками постоянно.
Все построения в ТММ выполняют в определённом масштабе. Масштаб какой-либо величины  , изображаемой отрезком , изображаемой отрезком  , характеризуют масштабным коэффициентом: , характеризуют масштабным коэффициентом:
 , (3.1) , (3.1)
где  выражают в единицах системы СИ – метр, килограмм, секунда, радиан т. д., выражают в единицах системы СИ – метр, килограмм, секунда, радиан т. д.,  – в миллиметрах. Таким образом, масштабный коэффициент – это цена одного миллиметра чертежа. – в миллиметрах. Таким образом, масштабный коэффициент – это цена одного миллиметра чертежа.
Графическое решение уравнения скорости точки  называется планом скоростей. Чтобы его построить, из произвольной точки называется планом скоростей. Чтобы его построить, из произвольной точки  , называемой полюсом плана скоростей, проводят вектор , называемой полюсом плана скоростей, проводят вектор  , изображающий скорость точки , изображающий скорость точки  (рис. 3.7, б). Длину (рис. 3.7, б). Длину  вектора выбирают произвольно. По формуле вектора выбирают произвольно. По формуле 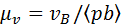 вычисляют масштабный коэффициент плана скоростей. Через точку вычисляют масштабный коэффициент плана скоростей. Через точку 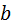 проводят линию действия вектора проводят линию действия вектора  . Искомая сумма выходит из полюса и идёт до упора в линию вектора . Искомая сумма выходит из полюса и идёт до упора в линию вектора  . По формуле . По формуле  вычисляют истинные значения скоростей вычисляют истинные значения скоростей  и и  . .
Угловые скорости звеньев 2, 3. Система координат B  движется поступательно. Ось движется поступательно. Ось  этой системы все время параллельна стойке. За любой промежуток времени звено 2 поворачивается относительно системы этой системы все время параллельна стойке. За любой промежуток времени звено 2 поворачивается относительно системы  и относительно стойки на один и тот же угол. Из этого следует, что абсолютная угловая скорость звена 2 равна относительной: и относительно стойки на один и тот же угол. Из этого следует, что абсолютная угловая скорость звена 2 равна относительной: 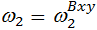 . В свою очередь . В свою очередь
 . Направление скорости . Направление скорости  указывает вектор указывает вектор  , изображающий скорость , изображающий скорость  . Первая буква в обозначении . Первая буква в обозначении  указывает начало вектора. Вектор указывает начало вектора. Вектор  , перенесённый по принадлежности в точку , перенесённый по принадлежности в точку  , «вращает» звено 2 вокруг точки , «вращает» звено 2 вокруг точки  по часовой стрелке, сюда и направлена скорость по часовой стрелке, сюда и направлена скорость  . .
Скорость звена 3 вычисляют по формуле  . Направление скорости . Направление скорости  определяют переносом в точку определяют переносом в точку  вектора вектора  , изображающего скорость , изображающего скорость  . .
Скорости мест присоединения цепи 4, 5. Местами присоединения являются точки 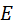 , ,  . На данный момент звенья 1, 2, к которым присоединяется группа, содержат по две точки с известными скоростями, это точки . На данный момент звенья 1, 2, к которым присоединяется группа, содержат по две точки с известными скоростями, это точки 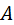 , ,  на звене 1 и на звене 1 и  , ,  на звене 2. Когда известны скорости двух точек какого-либо звена, скорость третьей точки определяют по теореме подобия, известной из теоретической механики. на звене 2. Когда известны скорости двух точек какого-либо звена, скорость третьей точки определяют по теореме подобия, известной из теоретической механики.
Теорема гласит: «Точки звена и концы абсолютных скоростей этих точек на плане скоростей образуют геометрически подобные и сходственно расположенные фигуры». Сходственность расположения означает одинаковость взаимного положения точек.
Прежде чем применять теорему к звену 1, необходимо указать на плане конец скорости точки 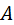 . Все абсолютные скорости на плане выходят из его полюса. Скорость точки . Все абсолютные скорости на плане выходят из его полюса. Скорость точки 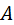 равна нулю, следовательно, конец вектора этой скорости находится в той же точке, где и начало, т. е. в полюсе. Имея это в виду, на стороне равна нулю, следовательно, конец вектора этой скорости находится в той же точке, где и начало, т. е. в полюсе. Имея это в виду, на стороне  плана строят треугольник плана строят треугольник  (читай (читай  ), подобный треугольнику ), подобный треугольнику  на схеме механизма. на схеме механизма.
Примечание. Для лучшей читаемости плана скоростей всё построенное на данном и последующих этапах выделено пунктирными линиями.
Из двух возможных треугольников, подобных  , выбирают сходственно расположенный. Сходственность расположения можно обеспечить, ориентируясь, например, на положение точки , выбирают сходственно расположенный. Сходственность расположения можно обеспечить, ориентируясь, например, на положение точки 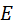 по отношению к стороне по отношению к стороне  : при наблюдении из точки : при наблюдении из точки  точка точка 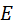 находится справа от прямой находится справа от прямой  , такое же положение должна занимать точка , такое же положение должна занимать точка  по отношению к прямой по отношению к прямой  , если смотреть из точки , если смотреть из точки 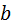 . .
Подобие и сходственность расположения можно обеспечить проще, если учесть взаимную перпендикулярность одноимённых сторон треугольников  и и  . На этом основании из точки . На этом основании из точки 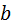 проводят прямую проводят прямую  , перпендикулярную , перпендикулярную  (точки (точки  ещё нет), а из точки ещё нет), а из точки 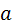 – прямую – прямую  , перпендикулярную , перпендикулярную 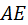 . На пересечении этих прямых получают точку . На пересечении этих прямых получают точку  . .
Переходя к звену 2, определяют скорость точки  . Для этого на стороне . Для этого на стороне  плана скоростей строят треугольник плана скоростей строят треугольник  , подобный и сходственно расположенный треугольнику , подобный и сходственно расположенный треугольнику 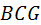 . Проблема сходственности решается здесь аналогично рассмотренной выше. . Проблема сходственности решается здесь аналогично рассмотренной выше.
Скорость точки 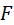 . С этого места решение задачи обретает общий характер, не знакомый по курсу теоретической механики. С местами присоединения цепи 4, 5 связывают системы координат . С этого места решение задачи обретает общий характер, не знакомый по курсу теоретической механики. С местами присоединения цепи 4, 5 связывают системы координат  и и  , движущиеся поступательно (см. рис. 3.7, а). Эти системы принимают за несущие для звеньев 4 и 5, соответственно. Говоря более подробно, считается, что движение звена 4 состоит из поступательного вместе с системой , движущиеся поступательно (см. рис. 3.7, а). Эти системы принимают за несущие для звеньев 4 и 5, соответственно. Говоря более подробно, считается, что движение звена 4 состоит из поступательного вместе с системой  и вращательного относительно этой системы. Аналогично раскладывается движение звена 5. Из принятых разложений движения вытекает система уравнений: и вращательного относительно этой системы. Аналогично раскладывается движение звена 5. Из принятых разложений движения вытекает система уравнений:
 (3.2) (3.2)
В этой системе 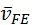 есть скорость точки есть скорость точки 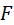 относительно системы координат относительно системы координат  и, следовательно, и, следовательно,  . Аналогично, . Аналогично,  . Чтобы решить систему уравнений, из полюса р (см. рис. 3.7, б) выстраивают две цепи векторов, стоящих в правой части уравнений. Первые слагаемые . Чтобы решить систему уравнений, из полюса р (см. рис. 3.7, б) выстраивают две цепи векторов, стоящих в правой части уравнений. Первые слагаемые 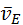 , ,  обоих уравнений уже построены. Остаётся провести через их концы обоих уравнений уже построены. Остаётся провести через их концы  , ,  линии действия вторых слагаемых линии действия вторых слагаемых 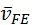 , ,  . Искомая сумма . Искомая сумма  начинается в полюсе начинается в полюсе  и заканчивается в точке пересечения и заканчивается в точке пересечения 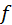 линий действия вторых слагаемых. линий действия вторых слагаемых.
На этом определение всех линейных скоростей закончено. Угловые скорости звеньев 4, 5 определяют так же, как для звена 2.
Ускорения точек  и и  (рис. 3.8, а). Ускорение точки (рис. 3.8, а). Ускорение точки  определяют непосредственно по исходным данным: определяют непосредственно по исходным данным:
 ; ;  ; ;  . .
Для определения ускорения точки  составляют два уравнения: составляют два уравнения:
 (3.3) (3.3)
Первое вытекает из разложения движения звена 2 на поступательное с системой  и вращательное относительно этой системы. Второе есть результат разложения ускорения точки и вращательное относительно этой системы. Второе есть результат разложения ускорения точки  на нормальную и тангенциальную составляющие. В первом уравнении отсутствует ускорение Кориолиса. Это объясняется поступательным движением системы на нормальную и тангенциальную составляющие. В первом уравнении отсутствует ускорение Кориолиса. Это объясняется поступательным движением системы  . .
Недостающие нормальные составляющие в обоих уравнениях определяют по формулам:  ; ;  . Направление этих составляющих – к центру кривизны соответствующей траектории. Так, составляющая . Направление этих составляющих – к центру кривизны соответствующей траектории. Так, составляющая  направлена от точки направлена от точки  к точке к точке  , составляющая , составляющая  – от точки – от точки  к к  . Тангенциальные составляющие перпендикулярны нормальным, но не известны по величине. Однако всего этого достаточно для решения системы (3.3). . Тангенциальные составляющие перпендикулярны нормальным, но не известны по величине. Однако всего этого достаточно для решения системы (3.3).
Как и в случае скоростей, из полюса  (рис. 3.8, б) выстраивают две цепи векторов, стоящих в правой части обоих уравнений системы (3.3). Этим цепям соответствуют ломаные (рис. 3.8, б) выстраивают две цепи векторов, стоящих в правой части обоих уравнений системы (3.3). Этим цепям соответствуют ломаные  и и 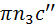 соответственно. Результирующий вектор проводят из полюса в точку пересечения соответственно. Результирующий вектор проводят из полюса в точку пересечения  последних слагаемых системы. последних слагаемых системы.
Рис. 3.8. Построение плана ускорений для двухзвенных
групп Ассура с вращательными парами
Буквой 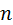 c цифровым индексом обозначены концы нормальных составляющих ускорений. Так, c цифровым индексом обозначены концы нормальных составляющих ускорений. Так,  , ,  , ,  – это концы составляющих – это концы составляющих  , ,  , ,  соответственно. Под прямым углом к нормальным составляющим располагаются тангенциальные. На взаимную перпендикулярность указывают знаки прямого угла, расположенные при каждой точке соответственно. Под прямым углом к нормальным составляющим располагаются тангенциальные. На взаимную перпендикулярность указывают знаки прямого угла, расположенные при каждой точке 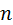 . .
Масштабы. Проведя вектор  , сразу же определяют масштабный коэффициент плана ускорений: , сразу же определяют масштабный коэффициент плана ускорений:  . Длины отрезков, изображающих . Длины отрезков, изображающих  и другие вычисленные выше ускорения, определяют по формуле и другие вычисленные выше ускорения, определяют по формуле  . Истинное значение любого ускорения, найденного из построений, находят по обратной формуле: . Истинное значение любого ускорения, найденного из построений, находят по обратной формуле:  . .
Угловые ускорения. Как и в случае угловых скоростей, абсолютное ускорение звена 2 равно относительному:  . В свою очередь, . В свою очередь,  . Направление ускорения . Направление ускорения  определяет вектор определяет вектор  , изображающий ускорение , изображающий ускорение  . Перенесённый по принадлежности в точку . Перенесённый по принадлежности в точку  , он «вращает» звено 2 по часовой стрелке, сюда и направлено ускорение , он «вращает» звено 2 по часовой стрелке, сюда и направлено ускорение  . .
Для звена 3 угловое ускорение 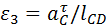 . Направление этого ускорения определяет вектор . Направление этого ускорения определяет вектор  , изображающий ускорение , изображающий ускорение  . Перенесенный по принадлежности в точку . Перенесенный по принадлежности в точку  , он «вращает» звено 3 , он «вращает» звено 3
по часовой стрелке, сюда и направлено ускорение 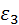 . На этом определение ускорений в цепи 2, 3 завершено. . На этом определение ускорений в цепи 2, 3 завершено.
Ускорения мест присоединения 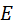 , ,  цепи 4, 5. Их определяют по теореме подобия, которая справедлива и для ускорений. Так, для определения ускорения точки цепи 4, 5. Их определяют по теореме подобия, которая справедлива и для ускорений. Так, для определения ускорения точки 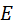 строят треугольник строят треугольник  (точка (точка 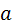 совпадает с полюсом совпадает с полюсом  ), подобный треугольнику ), подобный треугольнику  и сходственно с ним расположенный. Ускорение точки и сходственно с ним расположенный. Ускорение точки  определяют построением треугольника определяют построением треугольника  , подобного и сходственно расположенного с треугольником , подобного и сходственно расположенного с треугольником 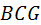 . В отличие от скоростей, подобные треугольники здесь не перпендикулярны друг другу, и воспользоваться упрощённым построением их невозможно. Чтобы не перегружать рисунок, стороны треугольника . В отличие от скоростей, подобные треугольники здесь не перпендикулярны друг другу, и воспользоваться упрощённым построением их невозможно. Чтобы не перегружать рисунок, стороны треугольника  не показаны, но отмечены его вершины. не показаны, но отмечены его вершины.
Примечание. Как и в случае плана скоростей, для лучшей читаемости плана ускорений всё построенное на данном и последующих этапах выделено пунктиром.
Ускорение точки 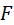 . Уравнения ускорений этой точки составляют на основе тех же разложений движения, что и при определении скоростей: . Уравнения ускорений этой точки составляют на основе тех же разложений движения, что и при определении скоростей:
 (3.4) (3.4)
Нормальные составляющие относительных ускорений определяют по формулам:  ; ;  . Входящие сюда относительные скорости берут из плана скоростей. Ускорение Кориолиса в обоих уравнениях равно нулю, т. к. носители звеньев 4, 5 движутся поступательно. Чтобы решить систему (3.4), из полюса . Входящие сюда относительные скорости берут из плана скоростей. Ускорение Кориолиса в обоих уравнениях равно нулю, т. к. носители звеньев 4, 5 движутся поступательно. Чтобы решить систему (3.4), из полюса  выстраивают две цепи векторов, стоящих в правой части уравнений. Первые слагаемые выстраивают две цепи векторов, стоящих в правой части уравнений. Первые слагаемые  , ,  обоих уравнений уже построены. Остаётся продолжить эти цепи и на пересечении получить конец обоих уравнений уже построены. Остаётся продолжить эти цепи и на пересечении получить конец 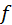 ускорения ускорения  . .
|



 и ускорение
и ускорение 
 ,
,  , а также угловые скорости и ускорения звеньев 2, 3.
, а также угловые скорости и ускорения звеньев 2, 3. . Всё необходимое для вычисления этой скорости есть. Для определения скорости точки
. Всё необходимое для вычисления этой скорости есть. Для определения скорости точки  , движущуюся поступательно. Эту систему принимают за носитель (переносчик) звена 2, т. е. считают, что абсолютное движение звена 2 – движение относительно стойки – состоит из поступательного вместе с системой
, движущуюся поступательно. Эту систему принимают за носитель (переносчик) звена 2, т. е. считают, что абсолютное движение звена 2 – движение относительно стойки – состоит из поступательного вместе с системой 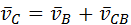 .
.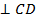


 относительно
относительно  , хотя в действительности это скорость точки
, хотя в действительности это скорость точки  . Скорость точки
. Скорость точки  , изображаемой отрезком
, изображаемой отрезком  , характеризуют масштабным коэффициентом:
, характеризуют масштабным коэффициентом: , (3.1)
, (3.1) , называемой полюсом плана скоростей, проводят вектор
, называемой полюсом плана скоростей, проводят вектор  , изображающий скорость точки
, изображающий скорость точки  вектора выбирают произвольно. По формуле
вектора выбирают произвольно. По формуле 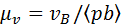 вычисляют масштабный коэффициент плана скоростей. Через точку
вычисляют масштабный коэффициент плана скоростей. Через точку 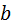 проводят линию действия вектора
проводят линию действия вектора  . Искомая сумма выходит из полюса и идёт до упора в линию вектора
. Искомая сумма выходит из полюса и идёт до упора в линию вектора  вычисляют истинные значения скоростей
вычисляют истинные значения скоростей  и
и  .
. движется поступательно. Ось
движется поступательно. Ось 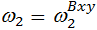 . В свою очередь
. В свою очередь  . Направление скорости
. Направление скорости  указывает вектор
указывает вектор  , изображающий скорость
, изображающий скорость  .
. . Направление скорости
. Направление скорости  определяют переносом в точку
определяют переносом в точку  , изображающего скорость
, изображающего скорость  .
.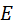 ,
,  . На данный момент звенья 1, 2, к которым присоединяется группа, содержат по две точки с известными скоростями, это точки
. На данный момент звенья 1, 2, к которым присоединяется группа, содержат по две точки с известными скоростями, это точки 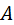 ,
,  (читай
(читай  ), подобный треугольнику
), подобный треугольнику  на схеме механизма.
на схеме механизма. : при наблюдении из точки
: при наблюдении из точки  по отношению к прямой
по отношению к прямой  , если смотреть из точки
, если смотреть из точки  , перпендикулярную
, перпендикулярную  (точки
(точки 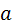 – прямую
– прямую  , перпендикулярную
, перпендикулярную 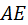 . На пересечении этих прямых получают точку
. На пересечении этих прямых получают точку  плана скоростей строят треугольник
плана скоростей строят треугольник  , подобный и сходственно расположенный треугольнику
, подобный и сходственно расположенный треугольнику 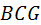 . Проблема сходственности решается здесь аналогично рассмотренной выше.
. Проблема сходственности решается здесь аналогично рассмотренной выше.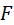 . С этого места решение задачи обретает общий характер, не знакомый по курсу теоретической механики. С местами присоединения цепи 4, 5 связывают системы координат
. С этого места решение задачи обретает общий характер, не знакомый по курсу теоретической механики. С местами присоединения цепи 4, 5 связывают системы координат  и
и  , движущиеся поступательно (см. рис. 3.7, а). Эти системы принимают за несущие для звеньев 4 и 5, соответственно. Говоря более подробно, считается, что движение звена 4 состоит из поступательного вместе с системой
, движущиеся поступательно (см. рис. 3.7, а). Эти системы принимают за несущие для звеньев 4 и 5, соответственно. Говоря более подробно, считается, что движение звена 4 состоит из поступательного вместе с системой  (3.2)
(3.2)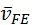 есть скорость точки
есть скорость точки  . Аналогично,
. Аналогично,  . Чтобы решить систему уравнений, из полюса р (см. рис. 3.7, б) выстраивают две цепи векторов, стоящих в правой части уравнений. Первые слагаемые
. Чтобы решить систему уравнений, из полюса р (см. рис. 3.7, б) выстраивают две цепи векторов, стоящих в правой части уравнений. Первые слагаемые 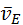 ,
,  обоих уравнений уже построены. Остаётся провести через их концы
обоих уравнений уже построены. Остаётся провести через их концы  линии действия вторых слагаемых
линии действия вторых слагаемых  . Искомая сумма
. Искомая сумма  начинается в полюсе
начинается в полюсе 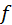 линий действия вторых слагаемых.
линий действия вторых слагаемых. ;
;  ;
;  .
. (3.3)
(3.3) ;
;  . Направление этих составляющих – к центру кривизны соответствующей траектории. Так, составляющая
. Направление этих составляющих – к центру кривизны соответствующей траектории. Так, составляющая  направлена от точки
направлена от точки  – от точки
– от точки  к
к  . Тангенциальные составляющие перпендикулярны нормальным, но не известны по величине. Однако всего этого достаточно для решения системы (3.3).
. Тангенциальные составляющие перпендикулярны нормальным, но не известны по величине. Однако всего этого достаточно для решения системы (3.3). (рис. 3.8, б) выстраивают две цепи векторов, стоящих в правой части обоих уравнений системы (3.3). Этим цепям соответствуют ломаные
(рис. 3.8, б) выстраивают две цепи векторов, стоящих в правой части обоих уравнений системы (3.3). Этим цепям соответствуют ломаные  и
и 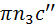 соответственно. Результирующий вектор проводят из полюса в точку пересечения
соответственно. Результирующий вектор проводят из полюса в точку пересечения  последних слагаемых системы.
последних слагаемых системы.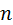 c цифровым индексом обозначены концы нормальных составляющих ускорений. Так,
c цифровым индексом обозначены концы нормальных составляющих ускорений. Так,  ,
,  ,
,  – это концы составляющих
– это концы составляющих  ,
,  , сразу же определяют масштабный коэффициент плана ускорений:
, сразу же определяют масштабный коэффициент плана ускорений:  . Длины отрезков, изображающих
. Длины отрезков, изображающих  и другие вычисленные выше ускорения, определяют по формуле
и другие вычисленные выше ускорения, определяют по формуле  . Истинное значение любого ускорения, найденного из построений, находят по обратной формуле:
. Истинное значение любого ускорения, найденного из построений, находят по обратной формуле:  .
. . В свою очередь,
. В свою очередь,  . Направление ускорения
. Направление ускорения  определяет вектор
определяет вектор  , изображающий ускорение
, изображающий ускорение  . Перенесённый по принадлежности в точку
. Перенесённый по принадлежности в точку  .
.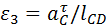 . Направление этого ускорения определяет вектор
. Направление этого ускорения определяет вектор  , изображающий ускорение
, изображающий ускорение  . Перенесенный по принадлежности в точку
. Перенесенный по принадлежности в точку 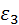 . На этом определение ускорений в цепи 2, 3 завершено.
. На этом определение ускорений в цепи 2, 3 завершено. (точка
(точка  и сходственно с ним расположенный. Ускорение точки
и сходственно с ним расположенный. Ускорение точки  (3.4)
(3.4) ;
;  . Входящие сюда относительные скорости берут из плана скоростей. Ускорение Кориолиса в обоих уравнениях равно нулю, т. к. носители звеньев 4, 5 движутся поступательно. Чтобы решить систему (3.4), из полюса
. Входящие сюда относительные скорости берут из плана скоростей. Ускорение Кориолиса в обоих уравнениях равно нулю, т. к. носители звеньев 4, 5 движутся поступательно. Чтобы решить систему (3.4), из полюса  ,
,  обоих уравнений уже построены. Остаётся продолжить эти цепи и на пересечении получить конец
обоих уравнений уже построены. Остаётся продолжить эти цепи и на пересечении получить конец  .
.


