
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы реечного зацепленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Образование зацепления. Реечное зацепление можно получить как результат преобразования колёсного зацепления. При преобразовании радиус основной окружности одного из колёс, например радиус При этом центр колеса 2 перемещается в точку
 : в сторону точки : в сторону точки  интерференция зацеплению не угрожает. Активная линия зацепления интерференция зацеплению не угрожает. Активная линия зацепления 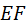 по-прежнему ограничивается линиями вершин зубьев. Угол зацепления по-прежнему ограничивается линиями вершин зубьев. Угол зацепления 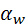 становится равным углу профиля рейки становится равным углу профиля рейки 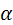 и, следовательно, не зависит от расстояния между колесом и рейкой. и, следовательно, не зависит от расстояния между колесом и рейкой.
Здесь и далее, Как в колёсном, так и в реечном зацеплении контактная нормаль совпадает с линией зацепления. Неизменность положения линии зацепления колеса с рейкой означает, что расстояние
Но как выражается это передаточное отношение через число зубьев
Рис. 5.6. Реечное эвольвентное зацепление Чтобы середина
Профилирование зубьев Метод обката С кинематической точки зрения все способы изготовления зубьев могут быть отнесены либо к методу копирования, либо к методу обката. При образовании профилей по методу копирования производимые профили представляют собой отпечаток, копию производящих профилей. Эту копию можно получить литьём, штамповкой, строганием, фрезерованием и другими технологическими способами. Недостаток метода копирования состоит в том, что каждому колесу, отличающемуся по числу зубьев хотя бы на единицу, нужен свой инструмент. В 1842 г. – это примерно на сто лет позже Эйлера – французский геометр Теодор Оливье показал, что одной и той же производящей поверхностью – в нашем случае производящим контуром ПК, перекатывающимся вместе с центроидой Ц 3 по центроидам Ц 1, Ц 2 производимого зацепления, можно образовать это зацепление с любым наперёд заданным числом зубьев
Рис. 5.7. Образование зацепления методом обката Метод, при котором производимое колесо является отпечатком производящего контура, перекатывающегося своей центроидой по центроиде производимого колеса, называется методом обката. При произвольном производящем контуре режущему или давящему инструменту соответствуют две производящие рейки Зацепление производимого колеса с производящим контуром называется станочным. Зацепление произведённых колёс друг с другом называется рабочим. На рис. 5.7 рабочим является зацепление 1, 2, станочными – зацепления 1, 3 и 2, 3. Теперь, когда рассмотрены свойства реечного зацепления
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

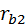 , увеличиваютдо
, увеличиваютдо  , оставив неизменными угол зацепления
, оставив неизменными угол зацепления 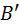 ; центр кривизны эвольвенты Э 2 в точке
; центр кривизны эвольвенты Э 2 в точке 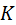 перемещается в точку
перемещается в точку 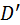 . Радиус кривизны эвольвенты Э 2 в точке
. Радиус кривизны эвольвенты Э 2 в точке 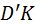 . Эвольвента Э 2 превращается в более спрямлённую эвольвенту Э¢ 2. Увеличение радиуса
. Эвольвента Э 2 превращается в более спрямлённую эвольвенту Э¢ 2. Увеличение радиуса 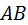 и
и 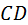 соответственно. Эвольвента Э 2 вырождается в прямую, перпендикулярную линии зацепления
соответственно. Эвольвента Э 2 вырождается в прямую, перпендикулярную линии зацепления 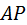 остаётся постоянным в любой фазе зацепления и при любом расстоянии между колесом и рейкой. Из равенства скоростей колеса и рейки в полюсе зацепления
остаётся постоянным в любой фазе зацепления и при любом расстоянии между колесом и рейкой. Из равенства скоростей колеса и рейки в полюсе зацепления 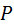 следует, что передаточное отношение
следует, что передаточное отношение .
. колеса и параметры рейки?
колеса и параметры рейки?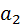 зуба рейки попала точно в середину
зуба рейки попала точно в середину 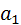 впадины колеса, шаг колеса
впадины колеса, шаг колеса 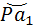 по центроиде Ц 1 должен быть равен шагу рейки
по центроиде Ц 1 должен быть равен шагу рейки  (на рисунке середина зуба рейки совпадает с полюсом
(на рисунке середина зуба рейки совпадает с полюсом  . Тогда центроида Ц 1, заполненная дугами
. Тогда центроида Ц 1, заполненная дугами  . В то же время,
. В то же время, 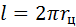 . Приравнивая правые части, получают:
. Приравнивая правые части, получают: 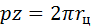 . Отсюда
. Отсюда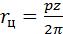 . (5.7)
. (5.7)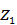 ,
, 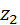 (рис. 5.7).
(рис. 5.7).


