
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Качественные характеристики эвольвентного зацепления
К о э ф ф и ц и е н т п е р е к р ы т и я. Как было сказано выше (см. рубрику 8.3), коэффициентом перекрытия называется отношение дуги зацепления к шагу. То и другое берётся по центроидной окружности. Применительно к эвольвентному зацеплению это отношение можно заменить отношением дуги зацепления по основной окружности к шагу по той же окружности. Основанием для такой замены служит положение о том, что если разделить числитель и знаменатель на радиус начальной окружности, то отношение не изменится. Отношение дуги зацепления к радиусу даст угол поворота зуба от начала до конца его контакта с соответствующим зубом другого колеса. Отношение шага к радиусу даст угловой шаг
Далее выразим длину отрезка H 1 H 2 следующим образом:
В этом выражении
Подставив вместо H 1 H 2 найденные значения слагаемых правой части, записываем
Заменим радиусы
Заменив радиусы
У д е л ь н о е с к о л ь ж е н и е. Удельным скольжением называется отношение скорости скольжения профилей в точке их касания к скорости перемещения точки касания по профилю. Этот показатель характеризует износ боковых (рабочих) поверхностей зубьев в результате трения скольжения. Об этом было сказано в рубрике 8.3. Там же было определено, что удельное скольжение описывается двумя математическими выражениями, относящимися к разным колёсам:
C учётом этого ранее записанные выражения примут следующий вид:
В этих выражениях буквой К обозначены совпадающие друг с другом точки К 1 и К 2.
Схематический график удельного скольжения показан на рис. 8.23.
К о э ф ф и ц и е н т у д е л ь н о г о д а в л е н и я. Коэффициентом удельного давления называется отношение модуля зацепления к приведённому радиусу кривизны профилей зубьев в точке их контакта. Этот коэффициент применяется при расчёте зубьев на контактную прочность. Формула Герца для расчёта контактных напряжений в контакте двух цилиндров имеет вид
где Умножив числитель и знаменатель формулы на модуль
где На основании свойств эвольвенты радиусы кривизны профилей равны:
Примерный вид графика коэффициента удельного давления в зависимости от положения точки контакта на линии зацепления показан на рис. 8.24.
Минимальное значение коэффициента q minполучается в центральной точке графика, то есть при
|
||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.232 (0.014 с.) |
 . Отношение дуги зацепления по основной окружности к радиусу этой окружности равно тому же углу поворота зуба, а отношение основного шага к радиусу основной окружности также равно угловому шагу
. Отношение дуги зацепления по основной окружности к радиусу этой окружности равно тому же углу поворота зуба, а отношение основного шага к радиусу основной окружности также равно угловому шагу  и определяется отношением
и определяется отношением .
.
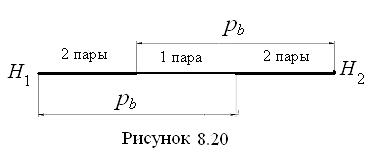 Обычно величина коэффициента перекрытия заключена между 1 и 2, при этом минимальное значение не должно быть меньше 1,1. Схематически соотношение между длиной
Обычно величина коэффициента перекрытия заключена между 1 и 2, при этом минимальное значение не должно быть меньше 1,1. Схематически соотношение между длиной  от точек H 1 и H 2, то отрезок H 1 H 2 будет разделён на три части. Две крайние части соответствуют зонам двухпарного зацепления зубьев, а средняя – зоне однопарного зацепления. Чем короче средняя зона, тем плавнее работает зубчатая передача, так как суммарная длина двух крайних участков становится длиннее. Данной формулой можно воспользоваться, если вычерчена картина зацепления пары колёс, на которой можно измерить отрезок H 1 H 2 и затем вычислить
от точек H 1 и H 2, то отрезок H 1 H 2 будет разделён на три части. Две крайние части соответствуют зонам двухпарного зацепления зубьев, а средняя – зоне однопарного зацепления. Чем короче средняя зона, тем плавнее работает зубчатая передача, так как суммарная длина двух крайних участков становится длиннее. Данной формулой можно воспользоваться, если вычерчена картина зацепления пары колёс, на которой можно измерить отрезок H 1 H 2 и затем вычислить  и
и 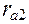 . Отмечены также радиусы основных окружностей
. Отмечены также радиусы основных окружностей  и
и  . И, наконец, указаны угол зацепления
. И, наконец, указаны угол зацепления  и профильные углы
и профильные углы  эвольвенты первого колеса на вершине зуба и
эвольвенты первого колеса на вершине зуба и 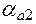 эвольвенты второго колеса также на вершине зуба. Сразу же отметим, что указанные профильные углы легко определяются из прямоугольных треугольников O 1 N 1 H 2 и O 2 N 2 H 1. Из первого треугольника находим
эвольвенты второго колеса также на вершине зуба. Сразу же отметим, что указанные профильные углы легко определяются из прямоугольных треугольников O 1 N 1 H 2 и O 2 N 2 H 1. Из первого треугольника находим  , из второго треугольника находим
, из второго треугольника находим 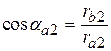 .
. .
. ,
,  ,
,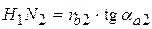 и
и  .
.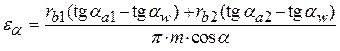 .
. .
.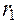 и
и  их выражениями через модуль и числа зубьев, а затем, поделив числитель и знаменатель на модуль
их выражениями через модуль и числа зубьев, а затем, поделив числитель и знаменатель на модуль 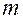 , окончательно получаем
, окончательно получаем .
. и
и  .
. Для определения тангенциальных составляющих скоростей обратимся к
Для определения тангенциальных составляющих скоростей обратимся к  , и перпендикулярно радиусу R 2 в сторону вращения колеса 2 отложим абсолютную скорость точки К 2, равную
, и перпендикулярно радиусу R 2 в сторону вращения колеса 2 отложим абсолютную скорость точки К 2, равную  . Отметим угол β 1 между радиусом R 1 и перпендикуляром O 1 N 1 к линии зацепления и β 2 – между радиусом R 2 и перпендикуляром О 2 N 2 также к линии зацепления. Спроецируем скорости
. Отметим угол β 1 между радиусом R 1 и перпендикуляром O 1 N 1 к линии зацепления и β 2 – между радиусом R 2 и перпендикуляром О 2 N 2 также к линии зацепления. Спроецируем скорости  и
и  на линию зацепления N 1 N 2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепочками равенств
на линию зацепления N 1 N 2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепочками равенств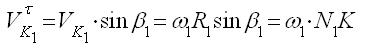 ,
,  .
. ,
,  .
.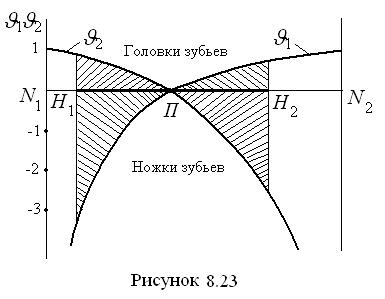 График показывает, что удельное скольжение на голов-ках зубьев меньше, чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении нахо-дится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относи-тельно другого, и точки профи-лей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.
График показывает, что удельное скольжение на голов-ках зубьев меньше, чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении нахо-дится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относи-тельно другого, и точки профи-лей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.
 – нормальное усилие, сжимающее цилиндры,
– нормальное усилие, сжимающее цилиндры,  – приведённый модуль упругости,
– приведённый модуль упругости,  – длина контактной линии цилиндров,
– длина контактной линии цилиндров,  – приведённый радиус кривизны цилиндров.
– приведённый радиус кривизны цилиндров.
 представляет собой коэффициент удельного давления.
представляет собой коэффициент удельного давления.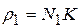 ;
;  , поэтому окончательно формула получится в виде
, поэтому окончательно формула получится в виде .
.
 . Это значение составляет величину
. Это значение составляет величину .
.


