Элементы относительного движения звеньев высшей пары

Ц е н т р о и д ы в о т н о с и т е л ь н о м д в и ж е н и и к о л ё с. Центроидой в движении одного колеса относительно другого, находящегося с ним в зацеплении, называется геометрическое место точек его мгновенного поворота относительно этого колеса.

Возьмём два зубчатых колеса, вращающихся вокруг центров O ₁ и O ₂ с угловыми скоростями ω ₁ и ω ₂ соответственно (рис. 8.1). В начальный момент окружности колёс касаются друг друга в точке П (греческая буква «пи»). Придадим обоим колёсам вращение с угловой скоростью – ω ₂, противоположной угловой скорости колеса 2 и равной ей по величине. Тогда колесо 2 станет неподвижным, а колесо 1 будет перекатываться по нему, и его центр будет занимать последовательно положения O ₁, O ^′₁, O ^′′₁,…, а точка касания окружностей будет перемещаться по окружности колеса 2, занимая положения П, П ^′, П ^′′,…, описывая, по существу, эту окружность. Причём окружность колеса 1 во всех своих положениях будет иметь мгновенным центром своего поворота точку П. Поэтому окружность Ц ₂ колеса 2 называется центроидой колеса 1 в его движении относительно колеса 2. Рассуждая точно так же, сделаем вывод, что и окружность Ц ₁ колеса 1 является центроидой колеса 2 в его движении относительно колеса 1. Индексы в обозначениях центроид указывают, в системе какого колеса находится центроида. Точка касания центроид в зацеплении называется полюсом зацепления П (пи).

О с н о в н о й з а к о н з а ц е п л е н и я (т е о р е м а В и л л и с а). Этот закон устанавливает связь между геометрией профилей зубьев и условиями передачи движения в зубчатом зацеплении (в более широком смысле – между геометрией элементов высшей пары и условиями передачи движения в механизме с высшей парой).

 

Возьмём две центроиды Ц ₁ и Ц ₂, принадлежащие колёсам 1 и 2 (рис. 8.2). Эти центроиды касаются друг друга в точке П, называемой полюсом зацепления.

Свяжем с центроидами профили Пр₁ и Пр₂ так, чтобы они касались друг друга в точке К. Относительная скорость точки К ₁ профиля Пр₁ по отношению к совпадающей с ней точке К ₂ профиля Пр₂, (в данный момент обе точки находятся на нормали n–n в точке K) обозначена на рис. 8.2 как V _отн. Примем во внимание следующие два положения:

1. Вектор перпендикулярен нормали, в противном случае появится составляющая относительной скорости, направленная вдоль неё. Если эта составляющая будет направлена в сторону Пр₂, то произойдёт внедрение профиля Пр₁ в профиль Пр₂, если она будет направлена в обратную сторону, то произойдёт отрыв профилей друг от друга. В обоих случаях высшая пара будет разрушена. Так что данное положение можно считать доказанным от противного.

2. Вектор перпендикулярен отрезку КП. Так как полюс П является мгновенным центром поворота центроиды Ц ₁ относительно центроиды Ц ₂, то, согласно положению теоретической механики, все точки, связанные с центроидой Ц ₁, имеют скорости, направленные перпендикулярно отрезку, соединяющему данную точку с центром (полюсом) поворота. Это и служит доказательством перпендикулярности вектора скорости и отрезка КП. Отсюда следует, что полюс зацепления – это не только точка касания центроид, но и точка пересечения контактной нормали профилей с линией центров колёс.

Доказанные положения позволяют сделать следующий вывод. Нормаль к профилям, проведённая в точке их касания, пересекает линию центров колёс в точке, совпадающей с полюсом зацепления, и таким образом делит межосевое расстояние центроид колёс на отрезки, обратно пропорциональные их угловым скоростям,

.

Другими словами, для правильной передачи движения с помощью высшей кинематической пары необходимо обеспечить такую форму её элементов, при которой нормаль к ним в точке контакта (контактная нормаль) проходила бы через полюс зацепления.

Профили, подчиняющиеся основному закону зацепления, называются сопряжёнными.

Следствие 1. Если полюс П занимает неизменное положение на линии центров колёс, то передаточное отношение постоянно, и радиусы центроид также постоянны. Это соответствует круглым зубчатым колёсам. В противном случае колёса некруглые.

Следствие 2. Если полюс П находится между центрами колёс, то они вращаются в противоположные стороны (внешнее зацепление колёс), и передаточное отношение имеет отрицательный знак.

Следствие 3. Если полюс П находится вне отрезка О ₁ О ₂, (выше или ниже этих центров), то колёса вращаются в одну сторону (внутреннее зацепление колёс).

Следствие 4. Относительная скорость в точке касания профилей по существу является скоростью скольжения профилей зубьев. Чем дальше от полюса находится точка касания профилей, тем больше в ней скорость скольжения. Если в процессе передачи движения точка контакта профилей совпадёт с полюсом, то в этот момент скорость скольжения будет равна нулю.

Существует большое количество профилей зубьев, удовлетворяющих этому закону. При выборе формы профилей руководствуются их технологичностью (простотой изготовления), простотой инструмента и расчетов.

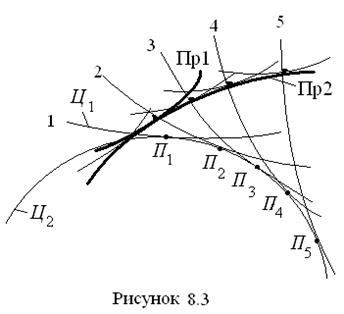П р о ф и л и з у б ь е в к а к в з а и м о о г и б а е м ы е к р и в ы е. Центроиды и один из профилей полностью определяют второй профиль. Если взять центроиды колёс Ц ₁ и Ц ₂ (рис. 8.3), и с центроидой Ц ₁ связать профиль Пр1, то, покатив эту центроиду с данным профилем по центроиде Ц ₂, получим второй профиль Пр2, принадлежащий второму колесу. На рис. 8.3 последовательное положение центроиды Ц ₁ отмечено цифрами 1, 2, 3, 4, 5, а её точки касания с центроидой Ц ₂ отмечены буквами П ₁, П ₂, П ₃, П ₄ и П ₅. В результате такого движения профиль Пр2 получается как огибающая ряда последовательных положений профиля Пр1.

Если поменять местами центроиды, то таким же образом можно получить и профиль зуба колеса 1 с помощью заданного профиля Пр2.

На рассмотренном положении основан один из методов изготовления зубьев колёс, причём Ц ₁ является центроидой инструмента, а Пр1 служит так называемым производящим исходным контуром.