
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика и синтез зубчатых механизмовСодержание книги
Поиск на нашем сайте С неподвижными осями колес Передаточное отношение сложного зубчатого механизма равно произведению передаточных отношений простых зубчатых передач, составляющих сложный механизм. Доказательство этого положения понятно из следующих выкладок:
Так как каждый из множителей правой части представляет собой передаточное отношение отдельных последовательно расположенных ступеней простых передач, то можно записать
что и требовалось доказать.
что после выполнения необходимых действий приводит к следующему результату
Этот результат показывает, что в механизмах такого типа передаточное отношение зависит только от чисел зубьев ведущего и ведомого колёс. Промежуточные колёса, числа зубьев которых не влияют на передаточное отношение, называются паразитными. Они позволяют только передать движение на небольшое расстояние и изменить его знак. Для общего случая механизма с произвольным числом колёс при вычислении передаточного отношения можно руководствоваться следующим выражением
где k – число внешних зацеплений, так как только они влияют на знак резуль-тата. Решение задачи синтеза (проектирования) механизмов данного типа заключается в подборе чисел зубьев ведущего и ведомого колёс для обеспечения заданного передаточного отношения. Что касается количества промежуточных колёс, то его выбирают исходя из расстояния между осями ведущего и ведомого колёс и необходимости экономии пространства, где размещается механизм. М е х а н и з м с о с т у п е н ч а т ы м с о е д и н е н и е м к о л ё с.
Никаких сокращений здесь нет кроме возможных общих множителей после подстановки чисел зубьев. Общий знак минус появился из-за того, что в механизме нечётное число пар внешнего зацепления (три пары). Для общего случая механизма запишем формулу передаточного отношения в следующем виде Такие механизмы более выгодны с точки зрения преобразования движения, чем механизмы с рядовым соединением колес, так как они позволяют получить любое передаточное отношение. Задача синтеза механизма заключается в разложении заданного передаточного отношения на множители, количество которых определяет количество ступеней (или пар колёс) в механизме, а величина каждого множителя определяет передаточное отношение соответствующей ступени. При этом величина множителя обеспечивается подбором чисел зубьев. Выбор количества ступеней (пар колёс) зависит от количества множителей и знака заданного передаточного отношения. Пример. Задано передаточное отношение
причём, все четыре ступени могут быть внешнего зацепления.
2.5. Кинематика механизмов планетарного типа
Т и п о в а я с х е м а э п и ц и к- л и ч е с к о г о м е х а н и з м а представлена на рис. 2.7. Она включает центральное колесо 1 с внешними зубьями, называемое также солнечным колесом, центральное колесо 3 с внутренними зубьями и колесо 2, называемое сателлитом. Сателлит получил своё название из-за двух вращательных движений, в которых он участвует: вращения вокруг собственной оси и вращения вокруг общей оси механизма. Такую возможность ему предоставляет звено H стержневого типа, называемое водилом. Если оба центральные колеса вращаются, то в механизме W = 2, и он называется дифференциальным. Если одно из центральных колёс заторможено, то W = 1, и механизм называется планетарным. Наиболее часто встречающиеся схемы механизмов планетарного типа в блочном представлении изображены на рис. 2.8. Схема А соответствует обыкновенному планетарному механизму, имеющему одно ведущее звено и одно ведомое при любом числе эпициклических ступеней. На схеме Б показана блок-схема дифференциального механизма с двумя ведущими и одним ведомым звеньями. На схеме В представлен так называемый дифференциальный механизм с замкнутым контуром, который составлен из одной или нескольких эпициклических ступеней, представляющих дифференциальную часть, и дополнительной кинематической цепи, соединяющей выходной вал механизма с одним из его входных валов. В результате такой связи в механизме остаётся одно ведущее и одно ведомое звенья.
А н а л и т и ч е с к и й р а с ч ё т к и н е м а т и к и. Задача аналитического расчёта кинематики заключается в определении угловой скорости ведомого звена в дифференциальном механизме, или в определении передаточного отношения в планетарном механизме. Исходными данными в первом случае служат угловые скорости (или частоты вращения) двух ведущих звеньев механизма и в обоих случаях – числа зубьев колёс. Для решения задачи применяют метод обращения движения, который заключается в том, что всему механизму вместе со стойкой сообщается движение с угловой скоростью, равной и противоположно направленной угловой скорости водила. Тогда при сохранении характера относительного движения звеньев водило останавливается, а все звенья получают угловые скорости, уменьшенные на угловую скорость водила. Механизм в таком случае превращается в условный механизм с неподвижными осями колес. Это позволяет составить следующую таблицу скоростей.
Записываем передаточное отношение от первого центрального колеса к третьему
Всё сказанное относится и к случаю, когда задаются не угловые скорости колёс, а их частоты вращения, так как соотношение между ними подчиняется простой формуле Из трех величин левой части две должны быть заданы, третья определяется решением данного уравнения. В планетарном механизме, как сказано выше, одно из центральных колес неподвижно. Если, например, принять колесо 3 с внутренними зубьями за неподвижное, то есть принять
Разделив почленно числитель на знаменатель и заменив отношения угловых скоростей обозначениями передаточных отношений, получим окончательно
т. е. передаточное отношение в планетарном механизме от любого центрального колеса к водилу равно единице минус передаточное отношение от этого центрального колеса к другому центральному колесу в механизме с условно неподвижным водилом. Замечание 1. При решении задачи кинематики одноступенчатого планетарного механизма (схема А рис. 2.8) и одноступенчатого дифференциального механизма (схема Б рис. 2.8) составляется и решается одно уравнение типа (б) или типа (а) соответственно. Если решается задача кинематики дифференциального механизма с замкнутым контуром (схема В рис. 2.8), то необходимо составить два уравнения, одно из которых относится к дифференциальной ступени, другое – к замыкающей кинематической цепи, и решать эти уравнения как систему двух уравнений с двумя неизвестными. Замечание 2. Если в механизме имеется несколько ступеней планетарного типа, то их необходимо рассматривать по отдельности, независимо друг от друга. Г р а ф и ч е с к и й р а с ч ё т к и н е м а т и к и. Методика графического расчёта основана на том, что окружные скорости центроидных окружностей колес, находящихся в зацеплении, одинаковы, а в точке касания окружностей их направления совпадают. Кроме того, во вращательной кинематической паре скорость её центра является общей для обоих звеньев, составляющих пару. Важно также, что скорость точки, совершающей вращательное движение вокруг неподвижной точки, линейно зависит от её расстояния до последней, то есть подчиняется формуле
На этой картине скорости строятся в масштабе На следующем этапе расчёта строится план угловых скоростей (рис. 2.9, б). Вблизи кинематической схемы проведём горизонтальную прямую и на некотором расстоянии от неё вниз возьмём произвольную точку P, из которой проведём прямые параллельно линиям распределения скоростей до пересечения с горизонталью в точках 1 и 2. Запишем цепочку равенств, имея в виду предыдущие рассуждения и подобие треугольников на картине зацепления и на плане
Учитывая начало этого равенства и его конец, можно сделать вывод, что отрезки, полученные на горизонтали, в некотором масштабе изображают угловые скорости колёс (отсюда и название построения). Для определения масштаба угловых скоростей необходимо угловую скорость На основе изложенной методики можно достаточно просто решить задачу кинематики любого зубчатого механизма. М е х а н и з м с о с т у п е н ч а т ы м с о е д и н е н и е м к о л ё с. Изобразим механизм, состоящий из четырёх колёс 1, 2, 2′ и 3, в некотором масштабе Для построения картины скоростей (рис. 2.10, б) вычислим скорость точки A:
Построение плана угловых скоростей затруднений не вызывает (рис. 2.10, в). Найденные на горизонтальной линии плана отрезки Если по условию задачи требуется определить только передаточное отношение механизма, то достаточно взять просто отношение соответствующих отрезков, измеренных на плане угловых скоростей. М е х а н и з м п л а н е т а р н о г о т и п а. Выберем одну из схем механизма планетарного типа и изобразим её в масштабе
Проведём горизонтальную линию от точки O 2 оси размеров до её пересечения с линией распределения скоростей колеса 2 в точке o 2. Так найдём линейную скорость точки O 2, которая является также скоростью точки O 2 водила. Поэтому, соединив точку o 2 с точкой O общей оси механизма, получим линию распределения скоростей водила H. Построение плана угловых скоростей механизма (рис. 2.11, в) не вызывает затруднений. Замечание. В дифференциальных механизмах с замкнутым контуром (схема В рис. 2.8), как правило, ведущим звеном является центральное колесо дифференциальной ступени, и построение картины линейных скоростей от этого колеса невозможно. Для решения задачи необходимо выбрать в качестве ведущего любое другое звено и задаться произвольно его окружной скоростью. После этого задача решается без затруднений. 2.6. Синтез механизмов планетарного типа Задача синтеза заключается в подборе чисел зубьев колёс механизма, обеспечивающих заданное отношение угловых скоростей входа и выхода. Заданными величинами должны быть или передаточное отношение (в планетарном механизме), или угловые скорости (частоты вращения) – в дифференциальном механизме. Используя уравнения (а) и (б), подставляя в их левую часть заданные значения, получают величину У с л о в и е с о о с н о с т и заключается в том, что в механизмах планетарного типа оба центральные колеса и водило должны иметь общую неподвижную ось. В схеме рис. 2.7 это условие даёт возможность записать такое равенство
Учитывая, что каждый радиус определяется формулой
можно заменить величины радиусов в приведённом выше выражении и после несложных преобразований записать
Таким образом, выбирая числа зубьев колёс, необходимо учитывать последнее соотношение. У с л о в и е с о с е д с т в а заключается в необходимости такого подбора чисел зубьев, чтобы сателлиты, связанные с одним водилом, при их количестве больше двух, не задевали друг друга. В противном случае механизм не может быть собран. Для вывода соответствующей зависимости обратимся к рис. 2.12. На рисунке показана центроидная окружность центрального колеса 1 радиуса После выполнения несложных преобразований получаем окончательно
Если сателлит 2 представляет собой блок из двух колёс, то в это неравенство в качестве
Обозначим количество сателлитов в механизме буквой K. Так как все колёса образуют одинаковые зацепления, то они имеют один модуль m и шаг
Сокращая оба выражения на p и складывая их левые и правые части, имеем
Левая часть полученного равенства является целым числом, поэтому правая часть должна быть также целым числом. В правой части
Выразив отсюда
что является математическим выражением условия сборки, то есть частное от деления суммы чисел зубьев центральных колёс на количество сателлитов Необходимо иметь в виду, что данное условие пригодно только для механизмов с одинарным сателлитом или со сдвоенным, но при одном модуле обоих колёс сателлита и сопряжённых с ними колёс. Для получения математического выражения условий сборки других схем можно обратиться к литературе. Подытоживая рассмотренные решения, запишем все математические условия, которые необходимо учитывать при синтезе зубчатых механизмов планетарного типа. Например, для схемы механизма (рис. 2.7) составляется следующая система уравнений с неравенством:
В заключение рассмотрим пример синтеза механизма планетарного типа, схема которого изображена на рис. 2.7. Решение приводится с привлечением компьютерного математического пакета MathCAD версии 2001i Professional (листинг 2.1). Вычислительная программа составлена в соответствии с методикой, описанной в инструкции к пакету. Так как системы уравнений решаются методом итераций, то необходимо в самом начале задать искомым переменным, в нашем случае z 1, z 2, z 3 и K, некоторые начальные значения. Они приведены ниже подзаголовка «Начальные условия». Затем идёт блок Given, в котором приведены вышеперечисленные уравнения и неравенство, связывающие между собой числа зубьев колёс и условия, которым они должны удовлетворять в механизме. Решающий блок Find содержитперечень искомых параметров и, после знака равенства, в виде матрицы автоматически выводятсянайденные значения этих параметров. В связи с тем, что числа зубьев колёс и количество сателлитов могут быть только целыми, то полученные значения необходимо округлить до целых, то есть принять Вопросы для самопроверки 1. Для чего применяются зубчатые механизмы? 2. Что такое передаточное отношение? 3. Какие зубчатые механизмы называют редукторами, мультипликаторами? 4. Как можно выразить передаточное отношение в паре зубчатых колёс? 5. Изобразите схему рядового, ступенчатого соединений зубчатых колёс. 6. Какая связь между передаточным отношением сложного зубчатого механизма и передаточными отношениями отдельных его ступеней? 7. Как определяется передаточное отношение в механизмах с рядовым и ступенчатым соединениями колёс? 8. Какие зубчатые механизмы являются механизмами планетарного типа (эпициклическими)? 9. В чём состоит основное достоинство механизмов планетарного типа? 10. Назовите элементы типовой схемы механизма планетарного типа. 11. Для чего и как применяется метод обращения движения? 12. Каковы особенности аналитического расчета механизмов планетарного типа различных схем? 13. Как выполняется синтез (проектирование) зубчатых механизмов с неподвижными осями колёс? 14. На чём основан графический метод исследования кинематики зубчатых механизмов? 15. Какова особенность графического расчёта кинематики дифференциального механизма с замкнутым контуром? 16. В чём заключаются условия соосности и соседства в механизмах планетарного типа? 17. Сформулируйте и объясните условие сборки при синтезе механизмов планетарного типа.
|
||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 670; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.200 (0.012 с.) |

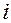 1 n =
1 n = 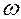 1 /
1 /  М е х а н и з м с р я д о в ы м с о е д и н е н и е м к о л е с.
М е х а н и з м с р я д о в ы м с о е д и н е н и е м к о л е с.  .Записав передаточные отношения отдельных ступеней
.Записав передаточные отношения отдельных ступеней  ,
,  и
и 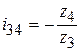 , и подставив их в правую часть полученного ранее произведения, имеем
, и подставив их в правую часть полученного ранее произведения, имеем ,
, .
. ,
,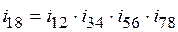 .
. Так как
Так как  и
и  , то, подставив в произведение передаточных отношений эти дроби, получим окончательно
, то, подставив в произведение передаточных отношений эти дроби, получим окончательно .
. , где k – число пар колёс внешнего зацепления, а символы в числителе означают произведение чисел зубьев ведомых колёс каждой пары, в знаменателе – произведение чисел зубьев ведущих колёс каждой пары.
, где k – число пар колёс внешнего зацепления, а символы в числителе означают произведение чисел зубьев ведомых колёс каждой пары, в знаменателе – произведение чисел зубьев ведущих колёс каждой пары.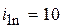 .Разложим это число на множители таким образом: i 1n = 10 = 2∙2∙2∙1,25. Из разложения видно, что в механизме может быть четыре ступени с передаточными отношениями:
.Разложим это число на множители таким образом: i 1n = 10 = 2∙2∙2∙1,25. Из разложения видно, что в механизме может быть четыре ступени с передаточными отношениями:
 ,
,  ,
,  ,
, В отличие от рассмотренных схем существуют механизмы, у которых оси отдельных колес подвижны. Такие механизмы относятся к механизмам планетарноо типа или эпициклическим. Эти механизмы по передаточному отношению выгодно отличаются от предыдущих, так как они могут обеспечить большое передаточное отношение при малом количестве колес (до 10 тысяч и более при четырех колесах).
В отличие от рассмотренных схем существуют механизмы, у которых оси отдельных колес подвижны. Такие механизмы относятся к механизмам планетарноо типа или эпициклическим. Эти механизмы по передаточному отношению выгодно отличаются от предыдущих, так как они могут обеспечить большое передаточное отношение при малом количестве колес (до 10 тысяч и более при четырех колесах).
 . (а)
. (а) , в которой n – это частота вращения, измеряемая в
, в которой n – это частота вращения, измеряемая в  . Поэтому в уравнении (а) угловые скорости можно заменить частотами вращения, что приведёт к уравнению
. Поэтому в уравнении (а) угловые скорости можно заменить частотами вращения, что приведёт к уравнению 
 .
. , (б)
, (б) . Зубчатые колёса, изображённые на рис. 2.9, а в некотором масштабе
. Зубчатые колёса, изображённые на рис. 2.9, а в некотором масштабе  , вращаются навстречу друг другу так, что в точке П касания их центроидных окружностей окружные скорости совпадающих точек П 1и П 2 также совпадают. Концы векторов скоростей
, вращаются навстречу друг другу так, что в точке П касания их центроидных окружностей окружные скорости совпадающих точек П 1и П 2 также совпадают. Концы векторов скоростей  точек, лежащих на прямой О 1 О 2, принадлежащих колесу 1, располагаются на одной прямой (рис. 2.9, а), называемой линией распределения скоростей этого колеса. То же имеет место и со скоростями точек колеса 2, концы векторов которых лежат на линии распределения скоростей, соединяющей точку O 2 центра колеса 2 с концом вектора скорости
точек, лежащих на прямой О 1 О 2, принадлежащих колесу 1, располагаются на одной прямой (рис. 2.9, а), называемой линией распределения скоростей этого колеса. То же имеет место и со скоростями точек колеса 2, концы векторов которых лежат на линии распределения скоростей, соединяющей точку O 2 центра колеса 2 с концом вектора скорости 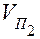 . Изображение линий распределения скоростей колёс механизма называется картиной скоростей.
. Изображение линий распределения скоростей колёс механизма называется картиной скоростей.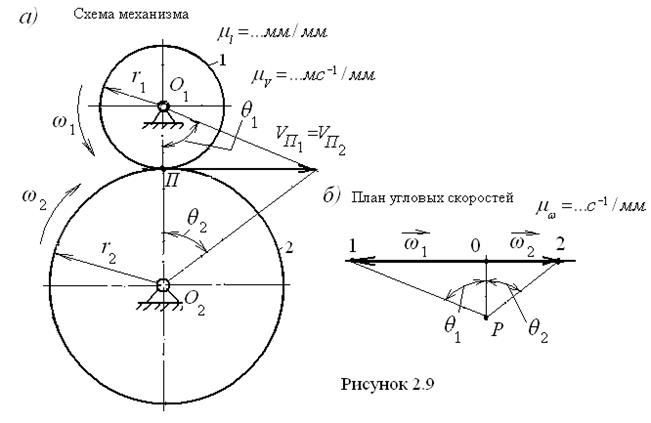
 .(Заметим в скобках, что масштабом в ТММ называется число, показывающее, сколько единиц какой-либо физической величины содержится в одном миллиметре её изображения. Изображение величины всегда производится в виде отрезка. Это могут быть векторы, ординаты и абсциссы графиков и т. д., измеряемые в миллиметрах. Масштабы, как видим, обозначаются буквой
.(Заметим в скобках, что масштабом в ТММ называется число, показывающее, сколько единиц какой-либо физической величины содержится в одном миллиметре её изображения. Изображение величины всегда производится в виде отрезка. Это могут быть векторы, ординаты и абсциссы графиков и т. д., измеряемые в миллиметрах. Масштабы, как видим, обозначаются буквой  с индексом, обозначающим соответствующую физическую величину. Например, масштаб скоростей
с индексом, обозначающим соответствующую физическую величину. Например, масштаб скоростей  читается: ноль целых две сотых метра в секунду в одном миллиметре изображения (или чертежа). Масштаб угловых скоростей
читается: ноль целых две сотых метра в секунду в одном миллиметре изображения (или чертежа). Масштаб угловых скоростей  читается: ноль целых одна сотая радиана в секунду в одном миллиметре).
читается: ноль целых одна сотая радиана в секунду в одном миллиметре).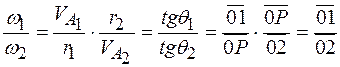 .
.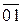 , измеренный в миллиметрах, т. е.
, измеренный в миллиметрах, т. е.  . Угловая скорость
. Угловая скорость  , взятый также в миллиметрах
, взятый также в миллиметрах  . План угловых скоростей даёт информацию и об их направлениях. В частности, на рис. 2.9, б видно, что угловые скорости колёс направлены в противоположные стороны.
. План угловых скоростей даёт информацию и об их направлениях. В частности, на рис. 2.9, б видно, что угловые скорости колёс направлены в противоположные стороны.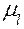 (рис. 2.10, а). Колёса вращаются вокруг центров O 1, O 2 и O 3, причём на промежуточном валу имеется два колеса 2 и 2′. Окружности колёс 1 и 2 касаются друг друга в точке A, а 2′ и 3 – в точке B. Известна угловая скорость
(рис. 2.10, а). Колёса вращаются вокруг центров O 1, O 2 и O 3, причём на промежуточном валу имеется два колеса 2 и 2′. Окружности колёс 1 и 2 касаются друг друга в точке A, а 2′ и 3 – в точке B. Известна угловая скорость 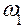 колеса 1. Справа от схемы механизма проведём вертикальную прямую, на которую снесём все отмеченные точки схемы, а именно: O 1, A, O 2, B и O 3. Расстояния между этими точками равны соответствующим радиусам колёс, поэтому данная прямая носит название оси размеров.
колеса 1. Справа от схемы механизма проведём вертикальную прямую, на которую снесём все отмеченные точки схемы, а именно: O 1, A, O 2, B и O 3. Расстояния между этими точками равны соответствующим радиусам колёс, поэтому данная прямая носит название оси размеров. и направим её вектор
и направим её вектор  вправо относительно оси размеров. Длина отрезка
вправо относительно оси размеров. Длина отрезка  рассчитывается по формуле
рассчитывается по формуле  c учётом предварительно выбранного масштаба
c учётом предварительно выбранного масштаба  . Через точку a конца этого вектора проводим линию распределения скоростей колеса 1 до точки O 1 и от этой же точки a проводим линию распределения скоростей колёс 2 и 2′ через точку O 2 и далее до горизонтали, проведённой от точки B механизма. Полученная на этой горизонтали точка b определяет вектор
. Через точку a конца этого вектора проводим линию распределения скоростей колеса 1 до точки O 1 и от этой же точки a проводим линию распределения скоростей колёс 2 и 2′ через точку O 2 и далее до горизонтали, проведённой от точки B механизма. Полученная на этой горизонтали точка b определяет вектор  скорости точки B. Величина этой скорости вычисляется как
скорости точки B. Величина этой скорости вычисляется как  . Для получения линии распределения скоростей колеса 3 достаточно соединить точку b с точкой O 3 на оси размеров.
. Для получения линии распределения скоростей колеса 3 достаточно соединить точку b с точкой O 3 на оси размеров.
 ,
,  и
и  в масштабе
в масштабе 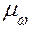 представляют векторы угловых скоростей
представляют векторы угловых скоростей  – колеса 1,
– колеса 1,  – колеса 2 (и 2′) и
– колеса 2 (и 2′) и  – колеса 3. Масштаб
– колеса 3. Масштаб  , вычисленного как
, вычисленного как  с учётом выбранного заранее масштаба
с учётом выбранного заранее масштаба 
 . Так как при неподвижном водиле получается механизм с неподвижными осями колёс, то для этого механизма задача подбора чисел зубьев на данном этапе ничем не отличается от ранее изложенных методик. Особенностью синтеза является необходимость учёта условий соосности, соседства и сборки.
. Так как при неподвижном водиле получается механизм с неподвижными осями колёс, то для этого механизма задача подбора чисел зубьев на данном этапе ничем не отличается от ранее изложенных методик. Особенностью синтеза является необходимость учёта условий соосности, соседства и сборки. .
. ,
,
 .
.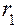 , по которой перекатываются центроидные окружности сателлитов 2 радиусов
, по которой перекатываются центроидные окружности сателлитов 2 радиусов  . Показаны также окружности вершин сателлитов радиусов
. Показаны также окружности вершин сателлитов радиусов 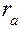 . Эти окружности по условию соседства не должны ни пересекаться, ни касаться друг друга. Сателлиты 2 находятся на угловом расстоянии γ (гамма)друг от друга. Так как сателлиты по окружности располагаются равномерно, то угол γ может быть определён из отношения
. Эти окружности по условию соседства не должны ни пересекаться, ни касаться друг друга. Сателлиты 2 находятся на угловом расстоянии γ (гамма)друг от друга. Так как сателлиты по окружности располагаются равномерно, то угол γ может быть определён из отношения  , где K – количество сателлитов, присоединённых к одному водилу. Половина расстояния между центрами сателлитов составляет
, где K – количество сателлитов, присоединённых к одному водилу. Половина расстояния между центрами сателлитов составляет 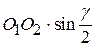 . Отрезок O 1 O 2 представляет собой длину водила или межосевое расстояние центрального колеса 1 и сателлита 2:
. Отрезок O 1 O 2 представляет собой длину водила или межосевое расстояние центрального колеса 1 и сателлита 2:  . Радиус окружности вершин
. Радиус окружности вершин  . Условие соседства выполняется, если выполняется неравенство
. Условие соседства выполняется, если выполняется неравенство  .
. .
. необходимо подставлять большее из них.
необходимо подставлять большее из них. У с л о в и е с б о р к и заключается в возможности собираемости механизма, то есть установки сателлитов, если их количество больше одного. Ясно, что один сателлит устанавливается между центральными колёсами беспрепятственно (если сателлитов несколько, то – первый из них). Чтобы установить второй и другие сателлиты, необходимо, чтобы их зубья вступали в зацепление с зубьями центральных колёс, а не натыкались на них, иначе сборка невозможна. Для решения задачи обратимся к рис. 2.13, на котором показаны участок центрального колеса 3 с внутренними зубьями, центральное колесо 1 и два параллельно работающих сателлита 2 из нескольких, расположенных по всему пространству между центральными колёсами 1 и 3.
У с л о в и е с б о р к и заключается в возможности собираемости механизма, то есть установки сателлитов, если их количество больше одного. Ясно, что один сателлит устанавливается между центральными колёсами беспрепятственно (если сателлитов несколько, то – первый из них). Чтобы установить второй и другие сателлиты, необходимо, чтобы их зубья вступали в зацепление с зубьями центральных колёс, а не натыкались на них, иначе сборка невозможна. Для решения задачи обратимся к рис. 2.13, на котором показаны участок центрального колеса 3 с внутренними зубьями, центральное колесо 1 и два параллельно работающих сателлита 2 из нескольких, расположенных по всему пространству между центральными колёсами 1 и 3.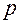 . Все центроидные окружности, показанные на рисунке, предполагаются делительными. Длина дуги A 1 B 1 окружности колеса 1 между точками касания этой окружности с окружностями сателлитов 2 составляет
. Все центроидные окружности, показанные на рисунке, предполагаются делительными. Длина дуги A 1 B 1 окружности колеса 1 между точками касания этой окружности с окружностями сателлитов 2 составляет  , то есть некоторое количество целых шагов
, то есть некоторое количество целых шагов  и возможную часть
и возможную часть  последнего неполного шага. Если на этой дуге помещается только целое количество шагов, то
последнего неполного шага. Если на этой дуге помещается только целое количество шагов, то  . Точно так же можно записать и длину дуги A 3 B 3 окружности колеса 3:
. Точно так же можно записать и длину дуги A 3 B 3 окружности колеса 3: 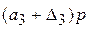 . С другой стороны, ясно, что эти дуги, при условии равномерного расположения осей сателлитов по окружности, составляют длины
. С другой стороны, ясно, что эти дуги, при условии равномерного расположения осей сателлитов по окружности, составляют длины  на окружности колеса 1 и
на окружности колеса 1 и  на окружности колеса 3. Приравнивая соответствующие выражения для колеса 1 и колеса 3, можно записать
на окружности колеса 3. Приравнивая соответствующие выражения для колеса 1 и колеса 3, можно записать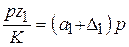 и
и 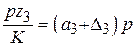 .
. .
. и K являются целыми числами, следовательно, доли шага
и K являются целыми числами, следовательно, доли шага  в сумме должны составить целое число, а именно – единицу. Так как сумма в квадратных скобках является целым числом, то её можно обозначить
в сумме должны составить целое число, а именно – единицу. Так как сумма в квадратных скобках является целым числом, то её можно обозначить  (от англ. integer – целое число), то есть
(от англ. integer – целое число), то есть  , и окончательно записать
, и окончательно записать .
. ,
, механизма должно быть целым числом.
механизма должно быть целым числом.




 ,
,  ,
, 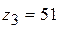 и
и 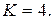 Естественно, что при округлении чисел зубьев изменяется передаточное отношение, поэтому последним шагом расчёта является проверка его величины. Она показала, что результат округления не привёл к ошибке передаточного отношения.
Естественно, что при округлении чисел зубьев изменяется передаточное отношение, поэтому последним шагом расчёта является проверка его величины. Она показала, что результат округления не привёл к ошибке передаточного отношения.


