
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование установившегося неравновесного движения машины с маховиком при силах – функциях перемещенийСодержание книги
Поиск на нашем сайте
В качестве исходных данных должны быть известны приведённые моменты движущих сил и сил сопротивления – В результате анализа требуется найти максимальное А н а л и т и ч е с к о е р е ш е н и е. На первом этапе решения определяется избыточная работа или по формуле На втором этапе решения определяется зависимость Таким образом, получается из уравнения в интегральной форме искомое выражение, из которого легко найти
Рассматривая один цикл установившегося движения машины, определяют По ним находят а затем – коэффициент неравномерности движения Г р а ф и ч е с к о е р е ш е н и е. Для графического решения задачи выберем прямоугольную систему координат (рис. 6.7), вдоль оси абсцисс которой в некотором масштабе При этом отрезок
Возьмём на кривой диаграммы энергомасс произвольную точку
или
Правая часть этого выражения совпадает с правой частью выражения (*), поэтому их левые части также одинаковы, то есть
Такие же расчёты можно сделать для любой другой точки диаграммы, поэтому можно утверждать, что прямая, соединяющая любую точку диаграммы энергомасс с истинным началом координат, образует с осью абсцисс этой диаграммы угол, тангенс которого пропорционален половине квадрата угловой скорости звена приведения (ведущего звена) в положении механизма, определяемом данной точкой. Сформулированное свойство диаграммы энергомасс позволяет определить угловую скорость входного звена механизма в любом его положении. Для определения
из которых находятся значения
Наконец, последний расчёт даёт
|
|||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.64.51 (0.005 с.) |

 и
и  , приведённый момент инерции механизмов машины –
, приведённый момент инерции механизмов машины – 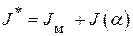 , включающий момент инерции маховика
, включающий момент инерции маховика  и переменную часть
и переменную часть  – приведённый момент инерции механизмов машины. Кроме этого должно быть задано начальное положение механизма, определяемое углом
– приведённый момент инерции механизмов машины. Кроме этого должно быть задано начальное положение механизма, определяемое углом 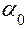 поворота ведущего звена, и значение угловой скорости ведущего звена в этом положении
поворота ведущего звена, и значение угловой скорости ведущего звена в этом положении 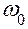 .
. и минимальное
и минимальное  значения угловой скорости, её среднюю величину
значения угловой скорости, её среднюю величину  и коэффициент
и коэффициент  неравномерности движения.
неравномерности движения. , или по формуле
, или по формуле  , в которой
, в которой 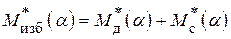 . При этом, если моменты заданы в виде графиков, что чаще всего бывает, то можно воспользоваться графическим интегрированием или способом площадей, как было описано выше, или другим известным способом.
. При этом, если моменты заданы в виде графиков, что чаще всего бывает, то можно воспользоваться графическим интегрированием или способом площадей, как было описано выше, или другим известным способом.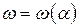 . Для
. Для 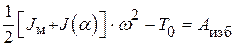 . В этом уравнении
. В этом уравнении  и представляет собой конкретное число, определяемое по исходным данным.
и представляет собой конкретное число, определяемое по исходным данным.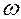
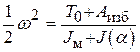 .
. 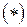
 значений угловой скорости, из которых выбирают
значений угловой скорости, из которых выбирают  ,
, .
.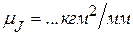 отложим значения
отложим значения  , а вдоль оси ординат – значения кинетической энергии
, а вдоль оси ординат – значения кинетической энергии  в масштабе
в масштабе  .
. оси абсцисс выражает момент инерции маховика, а отрезок
оси абсцисс выражает момент инерции маховика, а отрезок  оси ординат выражает величину кинетической энергии в начальный момент времени. Через правый конец отрезка
оси ординат выражает величину кинетической энергии в начальный момент времени. Через правый конец отрезка  , равное избыточной работе
, равное избыточной работе  . Для удобства дальнейших построений график избыточной работы разместим так, чтобы его ось абсцисс проходила на расстоянии
. Для удобства дальнейших построений график избыточной работы разместим так, чтобы его ось абсцисс проходила на расстоянии  . График
. График  из графиков
из графиков  называется диа
называется диа  граммой энергомасс.
граммой энергомасс.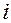 и соединим её с истинным началом O координат диаграммы. Отметим угол, образованный прямой Oi с осью абсцисс, как
и соединим её с истинным началом O координат диаграммы. Отметим угол, образованный прямой Oi с осью абсцисс, как  . Затем опустим перпендикуляр
. Затем опустим перпендикуляр  из точки
из точки  ,
, .
.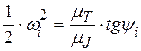 .
. и
и  необходимо провести из начала координат O прямые, касающиеся кривой графика сверху и снизу. Верхняя прямая образует с осью абсцисс угол
необходимо провести из начала координат O прямые, касающиеся кривой графика сверху и снизу. Верхняя прямая образует с осью абсцисс угол  , нижняя – угол
, нижняя – угол  , причём на основании предыдущего имеем следующие равенства:
, причём на основании предыдущего имеем следующие равенства:
 :
: .
. .
.


