
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виброгашение и виброизоляцияСодержание книги
Поиск на нашем сайте
В и б р о г а ш е н и е. Виброгашение представляет собой процесс устранения колебаний объекта без устранения источников этих колебаний. В некоторых технических устройствах устранение источников колебаний, например с помощью противовесов, по разным причинам невозможно. Вместе с тем существует необходимость гашения колебаний самого устройства в целом. Чтобы решить эту задачу, можно применить так называемое активное виброгашение, элементы которого функционируют на основе принципов работы систем автоматического управления (САУ). Другим вариантом решения является использование пассивного виброгашения, которое осуществляется с помощью так называемых динамических виброгасителей, или динамических гасителей колебаний, присоединяемых к устройству снаружи с помощью упругой связи.
Присоединим к данному устройству дополнительную массу 2 величиной Для вывода дифференциальных уравнений движения масс 1 и 2 воспользуемся уравнением Лагранжа II рода:
где Кинетическая энергия системы определяется суммой кинетических энергий масс Потенциальная энергия определяется следующим выражением Определим слагаемые уравнения Лагранжа
при при Обобщённая сила действует только на массу Найденные слагаемые позволяют получить следующую систему дифференциальных уравнений:
или
Эти уравнения описывают колебательные движения объекта 1 и гасителя 2. Так как колебания объекта с массой
Дифференцируя дважды эти выражения, получаем
Подставив в дифференциальные уравнения вместо координат и их вторых производных полученные выражения, после соответствующих сокращений можем записать
Решением данной системы двух алгебраических уравнений является определение амплитуд
и подставим результат в первое уравнение системы. После этого получается уравнение, содержащее только одно неизвестное
откуда находим Если знаменатель полученного выражения приравнять к нулю, то такое равенство называется частотным уравнением и его корни будут равны тем частотам, при которых амплитуда Равенство нулю амплитуды
Основание совершает колебания в вертикальной плоскости по некоторому закону Уравнение движения объекта при вибрации основания имеет вид
Данное уравнение по форме соответствует известному в теоретической механике основному уравнению динамики, где функция в правой части является суммой сил, действующих в системе. Эту сумму можно представить, как Подставив полученную сумму в правую часть уравнения, после деления его на
В этом уравнении
Данное уравнение является неоднородным дифференциальным уравнением, решение которого, как известно, равно сумме решения однородного уравнения (без правой части) и частного решения данного уравнения. Общее решение однородного уравнения можно опустить в силу того, что оно определяет собственные колебания объекта, которые быстро затухают. Частное решение для установившихся вынужденных колебаний получаем в виде
где
Дифференцирование выражения
Теперь определяем силу, передаваемую со стороны основания на объект
Множитель перед квадратными скобками можно разделить и умножить на
Коэффициент перед косинусом в квадратных скобках можно представить в виде Получившийся в виде множителя
Максимальное (амплитудное) значение силы
Отношение наибольшей силы, передаваемой на объект со стороны основания, к амплитуде вынуждающей силы называется коэффициентом передачи силы Из последней формулы видно, что равенство Коэффициент передачи силы характеризует качество виброзащитной системы. При жёстком соединении амортизируемого объекта и основания Исследования показывают, что, для того чтобы величина силы
Вопросы для самопроверки 1. Каков эффект неуравновешенности вращающихся масс в жёстких и нежёстких механических системах? 2. Каковы причины неуравновешенности вращающихся звеньев? 3. Каково воздействие неуравновешенных сил на фундамент машины? 4. Назовите и охарактеризуйте виды неуравновешенности вращающихся звеньев? 5. Как устраняется статическая неуравновешенность и статическая балансировка, динамическая неуравновешенность и балансировка? 6. Сколько противовесов требуется для статического уравновешивания, для динамического уравновешивания и почему? 7. Как осуществляется замена массы стержневого звена двумя точечными массами? 8. Как осуществляется статическое уравновешивание четырёхшарнирного механизма? 9. Какими способами осуществляется уравновешивание кривошипно-ползунного механизма? 10. Что такое самоуравновешенный механизм? 11. Как осуществляется частичное уравновешивание поступательно движущихся масс кривошипно-ползунного механизма? 12. Что такое виброгашение? В чём заключается принцип работы динамического гасителя колебаний? 13. Что такое виброизоляция? Как осуществляется защита объекта от колебаний основания? 14. Что такое коэффициент динамичности, коэффициент передачи силы? 15. При каком условии получается эффективной защита объекта от колебаний основания?
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1861; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.187 (0.012 с.) |

 Рассмотрим кратко теорию динамического гасителя колебаний. Представим себе, что имеется некоторое устройство 1 (рис. 7.18), имеющее массу
Рассмотрим кратко теорию динамического гасителя колебаний. Представим себе, что имеется некоторое устройство 1 (рис. 7.18), имеющее массу  и присоединённое к основанию с помощью упругой связи с коэффициентом жёсткости
и присоединённое к основанию с помощью упругой связи с коэффициентом жёсткости 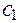 . Положение этого устройства относительно основания определяется координатой
. Положение этого устройства относительно основания определяется координатой  , измеряемой от некоторого начала отсчёта. На устройство действует вынуждающая сила
, измеряемой от некоторого начала отсчёта. На устройство действует вынуждающая сила 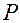 , изменяющаяся по гармоническому закону
, изменяющаяся по гармоническому закону  , где
, где 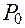 – амплитудное значение вынуждающей силы,
– амплитудное значение вынуждающей силы, 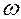 – круговая частота,
– круговая частота,  – время.
– время. с помощью упругой связи с коэффициентом жёсткости
с помощью упругой связи с коэффициентом жёсткости  . Положение массы
. Положение массы 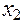 .
. ,
, – кинетическая энергия системы масс,
– кинетическая энергия системы масс,  – потенциальная энергия системы,
– потенциальная энергия системы,  – обобщённая координата,
– обобщённая координата,  – обобщённая скорость (производная обобщённой координаты по времени),
– обобщённая скорость (производная обобщённой координаты по времени), 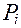 – обобщённая сила. Данная система имеет две степени свободы, поэтому i может приниматьтолько два значения:
– обобщённая сила. Данная система имеет две степени свободы, поэтому i может приниматьтолько два значения:  .
.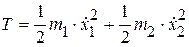 .
. .
. :
:  ,
,  ,
,  ,
,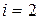 :
:  ,
, 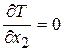 ,
,  .
.




 и
и 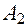 . Выразим из второго уравнения
. Выразим из второго уравнения 

 .
. . Если это явление наступает, то дополнительная масса
. Если это явление наступает, то дополнительная масса 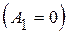 . Такое явление называется антирезонансом. Оно используется для гашения колебаний объекта при стабильной частоте вынуждающей силы путём подбора соответствующей массы гасителя
. Такое явление называется антирезонансом. Оно используется для гашения колебаний объекта при стабильной частоте вынуждающей силы путём подбора соответствующей массы гасителя  В и б р о и з о л я ц и я. Виброизоляцией называется процесс предотвращения передачи колебаний от основания к объекту (или наоборот), который установлен на этом основании. Виброизоляция осуществляется с помощью так называемых виброизоляторов, или амортизаторов. Зачастую такая задача возникает, когда некоторый объект устанавливается на колеблющемся фундаменте (рис. 7.19). Таким объектом может быть также автомобиль, движущийся по неровной дороге, когда его колёса совершают колебания в вертикальной плоскости и передаются кузову и сидящим в нём пассажирам. Задача амортизации здесь состоит в уменьшении динамической составляющей реакции со стороны основания на амортизируемый объект. Обозначим массу защищаемого объекта буквой
В и б р о и з о л я ц и я. Виброизоляцией называется процесс предотвращения передачи колебаний от основания к объекту (или наоборот), который установлен на этом основании. Виброизоляция осуществляется с помощью так называемых виброизоляторов, или амортизаторов. Зачастую такая задача возникает, когда некоторый объект устанавливается на колеблющемся фундаменте (рис. 7.19). Таким объектом может быть также автомобиль, движущийся по неровной дороге, когда его колёса совершают колебания в вертикальной плоскости и передаются кузову и сидящим в нём пассажирам. Задача амортизации здесь состоит в уменьшении динамической составляющей реакции со стороны основания на амортизируемый объект. Обозначим массу защищаемого объекта буквой 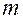 , коэффициент жёсткости упругой связи его с основанием обозначим
, коэффициент жёсткости упругой связи его с основанием обозначим  , коэффициент демпфирования амортизатора – буквой
, коэффициент демпфирования амортизатора – буквой 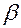 .
. . При этом на объект действует переменная сила
. При этом на объект действует переменная сила 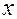 и его скорости
и его скорости  .
.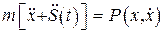 .
. , где первое слагаемое является силой упругости пружины, второе – силой сопротивления (силой трения) амортизатора. Отрицательные знаки в правой части указывают на противоположность действия этих сил по отношению к направлению движения объекта.
, где первое слагаемое является силой упругости пружины, второе – силой сопротивления (силой трения) амортизатора. Отрицательные знаки в правой части указывают на противоположность действия этих сил по отношению к направлению движения объекта. .
. , измеряется в
, измеряется в  ,
,  – квадрат частоты собственных колебаний объекта, измеряется в
– квадрат частоты собственных колебаний объекта, измеряется в  . Правая часть уравнения является второй производной функции кинематического возбуждения колебаний объекта со стороны основания. Её можно заменить отношением
. Правая часть уравнения является второй производной функции кинематического возбуждения колебаний объекта со стороны основания. Её можно заменить отношением  , где
, где  – внешняя сила, изменяющаяся по гармоническому закону, то есть
– внешняя сила, изменяющаяся по гармоническому закону, то есть  . Тогда предыдущее уравнение примет вид
. Тогда предыдущее уравнение примет вид .
.
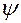 – сдвиг фаз силы и перемещения, определяемый выражением
– сдвиг фаз силы и перемещения, определяемый выражением

 .
. , тогда его можно представить как отношение амплитуды вынужденных колебаний перемещения
, тогда его можно представить как отношение амплитуды вынужденных колебаний перемещения  . Это отношение называется коэффициентом динамичности
. Это отношение называется коэффициентом динамичности 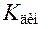 и определяется формулой
и определяется формулой .
. и обозначить тангенсом некоторого угла
и обозначить тангенсом некоторого угла 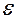 , то есть
, то есть  . Тогда этот коэффициент можно заменить тангенсом, а после соответствующих преобразований выражение в квадратных скобках поменяется на синус суммы углов, то есть
. Тогда этот коэффициент можно заменить тангенсом, а после соответствующих преобразований выражение в квадратных скобках поменяется на синус суммы углов, то есть  .
. в выражении силы
в выражении силы  и находим окончательное выражение для расчёта силы
и находим окончательное выражение для расчёта силы  .
.
 . В данном случае
. В данном случае 
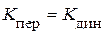 имеет место только при
имеет место только при 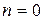 , то есть при отсутствии демпфирования.
, то есть при отсутствии демпфирования. . При
. При 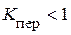 виброзащитная система эффективна, так как
виброзащитная система эффективна, так как  , при
, при  применение амортизатора нецелесообразно, так как приводит к увеличению передаваемого усилия.
применение амортизатора нецелесообразно, так как приводит к увеличению передаваемого усилия. . Обычно принимают
. Обычно принимают 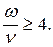 Это означает, что для эффективной защиты объекта от колебаний основания (эффективной амортизации объекта) необходимо, чтобы собственная частота колебаний системы была существенно меньше частоты колебаний основания.
Это означает, что для эффективной защиты объекта от колебаний основания (эффективной амортизации объекта) необходимо, чтобы собственная частота колебаний системы была существенно меньше частоты колебаний основания.


