Особенности зацепления эвольвентных косозубых колёс

 

Эвольвентные косозубые цилиндрические колёса предназначены для передачи вращения между параллельными осями (рис. 8.30, а). Каждое из колёс пары, образующей зацепление, имеет зубья, направленные не параллельно оси колеса, как у прямозубых колёс, а под некоторым углом к ней. Причём, как видно из рисунка, зубья расположены у колеса 1 под углом к его оси, у колеса 2 – под углом . Угол наклона зуба принимается равным от 8º до 35º.

Такое расположение зубьев приводит к плавному постепенному входу в зацепление и снижает динамические нагрузки (появляется дополнительное осевое перекрытие зубьев, повышающее плавность работы передачи). Особенности зацепления косозубых колёс позволяют полнее использовать свойства материалов и при тех же размерах колёс передавать мощность, большую, чем при прямозубых колёсах.

Недостатком косозубых колёс является возникающая в зацеплении дополнительная осевая сила, отсутствующая у прямозубых колёс.

 

 

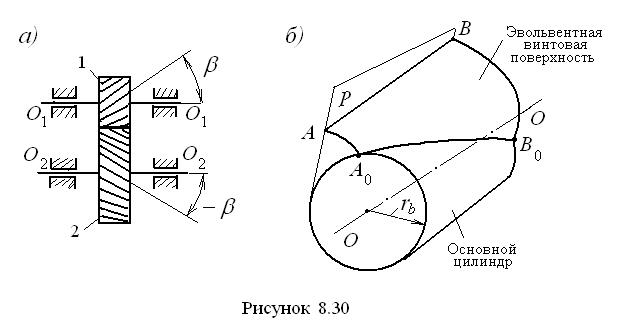
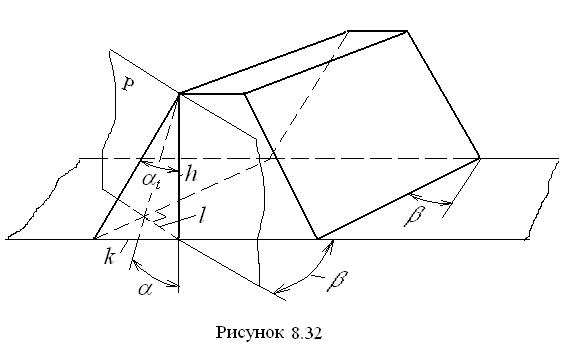
Боковые (рабочие) поверхности косозубых колёс, как и прямозубых, образуются на базе основных цилиндров (рис. 8.30, б). Их образование можно представить так. С основным цилиндром радиуса 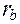вводится в касание плоскость P, в которой имеется прямая линия AB, не параллельная образующей основного цилиндра. При перекатывании без скольжения плоскости P по цилиндру прямая AB описывает эвольвентную винтовую поверхность, которая и служит рабочей поверхностью зуба колеса. В сечении этой поверхности любым круглым цилиндром, соосным с основным, в том числе и самим основным (линия A ₀ B ₀), получается винтовая линия. Поэтому косозубое колесо, по существу, является винтовым. Развернув косозубое колесо на плоскость, получим косозубую рейку, участок которой показан на рис. 8.31 и на которой видны особенности продольной формы зуба. Колесо имеет три шага – нормальный 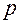, торцевой 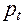и осевой . Нормальный шаг расположен в плоскости, перпендикулярной к линии зуба. След этой плоскости, совпадающий с нормалью к линии зуба, на рисунке обозначен n – n. Торцовый шаг расположен в торцовой плоскости колеса, осевой – в плоскости, содержащей ось колеса, или параллельной оси колеса при его развёртке в рейку (рис. 8.31). Поделив каждый из шагов на π, получим три модуля, из которых стандартным является нормальный модуль , он равен модулю инструмента, нарезающего колесо. Из рис. 8.31 видно, что , и 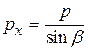. Соответствующие модули определяются по формулам и .

 

Для определения угла профиля зуба в торцовой плоскости обратимся к
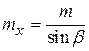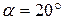рис. 8.32. В плоскости нормального сечения P угол профиля составляет . В торцовом же сечении угол профиля может быть определён как . Так как из прямоугольных треугольников можно последовательно записать , то формула для расчёта через тангенс получается как . Поскольку 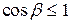, то , причём равенство этих углов имеет место в прямозубой передаче, когда . В косозубой передаче 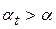, поэтому , и при равенстве высот зубьев в прямозубой и косозубой передачах, согласно формуле 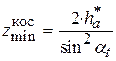, имеем . Например, при , , угол при этом значении тангенса составляет величину, равную . Далее определяем и . Допуская минимальный подрез, округляем полученное число до ближайшего целого: . Как известно, при стандартных размерах режущего инструмента 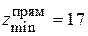, что существенно больше чем 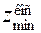. При других значениях угла наклона зуба получаются другие минимальные числа зубьев, но при любом они меньше 17.

Из качественных показателей зацепления необходимо отметить высокую плавность работы. Это связано с повышенной величиной коэффициента перекрытия, который определяется двумя слагаемыми:

.

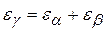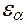Здесь – коэффициент торцового перекрытия, определяемый по формуле, применяемой для расчёта коэффициента перекрытия прямозубого зацепления; – коэффициент перекрытия в осевом направлении, определяемый отношением ( – ширина зубчатого венца колеса). Максимальное значение коэффициента перекрытия достигает значений от 10 до 20.

Следует отметить, что все размеры зубьев косозубого колеса определяются в торцовом сечении по формулам прямозубого колеса. Удельные скольжения и коэффициент удельного давления вычисляются по тем же формулам, что и для зацепления прямозубых колёс.