
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трение во вращательной кинематической пареСодержание книги
Поиск на нашем сайте
Рассмотрим вращательную кинематическую пару в наиболее часто встречающемся случае, когда сопряжение вала с отверстием осуществляется с зазором (рис. 5.11). На указанном рисунке зазор между валом и отверстием весьма преувеличен для того, чтобы лучше видеть элементы сопряжения. Вал нагружен поперечной силой Сопротивление вращению вала создаётся моментом трения Значение круга трения заключается в том, что полная реакция во вращательной паре проходит по касательной к нему, никогда не пересекая его. При этом её направление таково, что момент реакции относительно центра вала направлен против скорости вращения вала. Р а с ч ё т п о т е р ь м о щ н о с т и н а т р е н и е в о в р а щ а т е л ь -н о й п а р е. Реакции в кинематических парах, вычисляемые с помощью методов планов сил и других методов, являются, по существу, нормальными реакциями, так как они определялись в предположении отсутствия трения. Это значит, что коэффициент трения предполагался равным нулю, и, соответственно угол трения
Трение качения
Как было указано выше, трение качения относится к трению II рода и является характерным для высших кинематических пар. Происхождение сопротивления при качении можно объяснить следующим образом. Предположим, имеется каток (цилиндр) на плоскости (рис. 5.13). Если и цилиндр, и плоскость – абсолютно твёрдые тела, то в их контакте нет никаких деформаций, и они касаются друг друга в точке A. При этом, если на каток действует вертикальная сила Q (рис. 5. 13, а), то она вызывает появление реакции Реакция плоскости приложена точно в точке A её касания с цилиндром. Однако, в связи с тем, что абсолютно твёрдые тела в природе не существуют, в месте касания цилиндра и плоскости образуется площадка смятия A–B, на которой, согласно Г. Герцу, при неподвижном цилиндре давление распределяется по закону эллипса (рис. 5.13, б). Равнодействующая сил этого распределения
Расстояние Дерево по дереву………………………………………0,05 – 0,06 Дерево по стали………………………………………..0,03 – 0,04 Сталь по стали…………………………………………0,005 Чугун по чугуну……………………………………….0,005 Ролики или шарики из закалённой стали по стали….0,0005 – 0,0010
Потери мощности на трение качения определяются произведением момента трения качения на угловую скорость качения, то есть Вопросы для самопроверки 1. Назовите виды трения, характерные для низших, высших кинематических пар. 2. Как объяснить наличие трения скольжения? 3. Каким закономерностям подчиняется трение скольжения? 4. Как вычисляется сила трения скольжения? 5. Что такое коэффициент трения? От чего зависит величина коэффициента трения? 6. Что такое угол трения, конус трения? 7. Какую роль играют угол и конус трения в поступательной паре? 8. При каком условии движущая сила не может осуществить движение ползуна по плоскости? 9. В каком случае наклонная плоскость является самотормозящейся? 10. Что такое КПД? 11. Что такое коэффициент потерь? 12. Что такое приведённый коэффициент трения клинчатого ползуна? 13. Как определяется мощность трения в поступательной паре? 14. Как определяется КПД винтовой пары? 15. Что такое круг трения во вращательной паре? 16. В чём значение круга трения во вращательной паре? 17. В чём существо трения качения? 18. Как определить момент трения качения? 19. Как определить мощность трения качения? 20. Как определяется КПД механизма?
Динамика машин
В динамике рассматривается движение машин (или механизмов) в связи с силами, действующими на их звенья. Основными задачами этого раздела являются: 1. Определение фактической угловой скорости ведущего звена механизма. 2. Определение момента инерции маховика, необходимого для поддержания изменения угловой скорости в заданных пределах. 3. Уравновешивание и балансировка вращающихся звеньев. 4. Уравновешивание механизмов. 5. Виброзащита и виброизоляция машин и устройств.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.190 (0.011 с.) |


 , которая является известной величиной. При отсутствии вращения окружность вала касается окружности отверстия в точке
, которая является известной величиной. При отсутствии вращения окружность вала касается окружности отверстия в точке  на его вертикальном диаметре. Когда вал вращается в направлении
на его вертикальном диаметре. Когда вал вращается в направлении 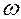 , то, в результате действия силы трения
, то, в результате действия силы трения 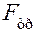 , он «взбирается» на стенку вала и в равновесном состоянии устанавливается, касаясь окружности отверстия в точке
, он «взбирается» на стенку вала и в равновесном состоянии устанавливается, касаясь окружности отверстия в точке  . При этом реакция
. При этом реакция 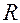 стенки отверстия равна и противоположна силе
стенки отверстия равна и противоположна силе 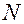 направлена вдоль нормали в точке касания окружностей, то есть вдоль линии, проходящей через точку касания и их центры. Сила трения направлена по касательной к окружностям, проходящей также через точку касания
направлена вдоль нормали в точке касания окружностей, то есть вдоль линии, проходящей через точку касания и их центры. Сила трения направлена по касательной к окружностям, проходящей также через точку касания  , равным произведению силы трения на радиус цапфы, то есть
, равным произведению силы трения на радиус цапфы, то есть  . Сила трения, как известно, определяется формулой
. Сила трения, как известно, определяется формулой 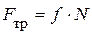 . Из силового треугольника по теореме Пифагора имеем
. Из силового треугольника по теореме Пифагора имеем  , или
, или  , откуда
, откуда  . Поэтому сила трения
. Поэтому сила трения  , а момент трения
, а момент трения 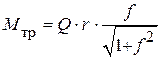 . Так как коэффициент трения
. Так как коэффициент трения  , то
, то  , тогда
, тогда  (например,
(например, 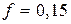 ,
, 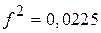 , а
, а  ). Поэтому можно принять, что
). Поэтому можно принять, что 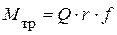 . Произведение радиуса цапфы на коэффициент трения является для данных условий постоянной величиной, определяемой только геометрией вала и условиями трения. Эта величина измеряется в линейных единицах, обозначается
. Произведение радиуса цапфы на коэффициент трения является для данных условий постоянной величиной, определяемой только геометрией вала и условиями трения. Эта величина измеряется в линейных единицах, обозначается  и называется кругом трения, который описывается этим радиусом при вращении вала (круг трения на рис. 5.11 заштрихован). Так что радиус круга трения
и называется кругом трения, который описывается этим радиусом при вращении вала (круг трения на рис. 5.11 заштрихован). Так что радиус круга трения  . Таким образом, при известном
. Таким образом, при известном  .
.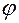 также принимался равным нулю. Поэтому для определения мощности трения
также принимался равным нулю. Поэтому для определения мощности трения  необходимо знать момент силы трения и относительную угловую скорость одного звена пары по отношению к другому, то есть
необходимо знать момент силы трения и относительную угловую скорость одного звена пары по отношению к другому, то есть  . Представим на рис. 5.12 вращательную пару, образованную звеньями 1 и 2, с увеличенным изображением её элементов. Предположим, что касание элементов пары происходит в точке A. В этой точке действуют реакции
. Представим на рис. 5.12 вращательную пару, образованную звеньями 1 и 2, с увеличенным изображением её элементов. Предположим, что касание элементов пары происходит в точке A. В этой точке действуют реакции 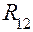 со стороны первого звена на второе и
со стороны первого звена на второе и 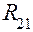 со стороны второго звена на первое. В этой же точке приложена сила трения
со стороны второго звена на первое. В этой же точке приложена сила трения 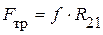 (здесь и далее имеется в виду, что рассматривается движение второго звена относительно первого, а не наоборот). Из рисунка видно, что момент трения
(здесь и далее имеется в виду, что рассматривается движение второго звена относительно первого, а не наоборот). Из рисунка видно, что момент трения 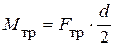 , где d – диаметр цапфы вала. Относительная угловая скорость
, где d – диаметр цапфы вала. Относительная угловая скорость  определяется с помощью метода обращения движения: если обоим звеньям пары сообщить движение с угловой скоростью, равной и противоположно направленной угловой скорости звена 1, то это звено остановится, а второе будет вокруг него вращаться с угловой скоростью
определяется с помощью метода обращения движения: если обоим звеньям пары сообщить движение с угловой скоростью, равной и противоположно направленной угловой скорости звена 1, то это звено остановится, а второе будет вокруг него вращаться с угловой скоростью  , которая и будет относительной скоростью звена 2 относительно звена 1. Таким образом, мощность трения, равная
, которая и будет относительной скоростью звена 2 относительно звена 1. Таким образом, мощность трения, равная  , окончательно выразится формулой
, окончательно выразится формулой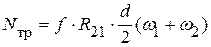 .
.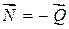 .
.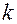 . Этот момент и препятствует качению цилиндра. Смещение равнодействующей вызвано наличием упругого гистерезиса в материале цилиндра и плоскости, причиной которого является внутреннее трение в материале. В результате перед катящимся цилиндром возникает подпорная волна (редан), которая и смещает результирующую реакцию.
. Этот момент и препятствует качению цилиндра. Смещение равнодействующей вызвано наличием упругого гистерезиса в материале цилиндра и плоскости, причиной которого является внутреннее трение в материале. В результате перед катящимся цилиндром возникает подпорная волна (редан), которая и смещает результирующую реакцию.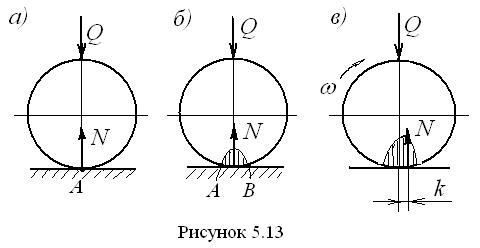
 У с л о в и я п е р е х о д а т р е н и я к а ч е н и я в т р е н и е с к о л ь- ж е н и я. Из практики известно, что если к цилиндру, находящемуся на плоскости, приложить силу
У с л о в и я п е р е х о д а т р е н и я к а ч е н и я в т р е н и е с к о л ь- ж е н и я. Из практики известно, что если к цилиндру, находящемуся на плоскости, приложить силу 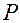 достаточно высоко от плоскости, то цилиндр будет катиться. Если силу приложить очень низко, то цилиндр будет скользить по плоскости, но не катиться. Выясним, при каких условиях возможно качение, и при каких – скольжение. Для этого обратимся к рис. 5.14. На нём показан цилиндр на плоскости, на который действует сверху вниз сила Q, нормальная реакция плоскости N, равная силе Q, сила трения
достаточно высоко от плоскости, то цилиндр будет катиться. Если силу приложить очень низко, то цилиндр будет скользить по плоскости, но не катиться. Выясним, при каких условиях возможно качение, и при каких – скольжение. Для этого обратимся к рис. 5.14. На нём показан цилиндр на плоскости, на который действует сверху вниз сила Q, нормальная реакция плоскости N, равная силе Q, сила трения  , скольжение требует обратного неравенства:
, скольжение требует обратного неравенства:  . Сила трения
. Сила трения  . Составим уравнение равновесия цилиндра в форме моментов:
. Составим уравнение равновесия цилиндра в форме моментов:  . Из этого уравнения получаем
. Из этого уравнения получаем  . Тогда условие качения получится как
. Тогда условие качения получится как  , или
, или  . Так как
. Так как 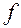 являются величинами постоянными, а изменить можно только
являются величинами постоянными, а изменить можно только  , то условие качения целесообразно записать в виде
, то условие качения целесообразно записать в виде  . Обратное неравенство соответствует условию скольжения:
. Обратное неравенство соответствует условию скольжения:  .
. . Момент трения качения равен произведению
. Момент трения качения равен произведению 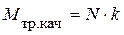 , или
, или  , поэтому окончательно
, поэтому окончательно  .
.


