
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование пуска машины при силах – функциях перемещенийСодержание книги
Поиск на нашем сайте
Для исследования задаются в форме графиков (рис. 6.6):
а также
Так как правая часть уравнения является избыточной работой, то для краткости записи уравнение можно представить в форме Как правило, функции приведенных моментов сил выражаются сложными зависимостями от Изобразим графики моментов сил в положительной области системы координат (рис. 6.6, а), перенеся условно график Согласно приведённой выше формуле, для расчёта угловой скорости необходимо вычислить избыточную работу в каждом положении механизма. Она вычисляется через площадки, ограниченные ординатами соседних значений
где
Чёрточки сверху над членами данной формулы указывают на то, что эти члены должны подставляться в виде отрезков, взятых с графика (рис. 6.6, а).
Вычисления по этим формулам дают следующие результаты: Далее получается:
и т. д.
Подставив полученные значения избыточной работы в приведённую выше формулу и взяв в соответствующем положении с графика (рис. 6.6, б) величину На следующем этапе анализа необходимо найти зависимость времени перехода машины из одного положения в соседнее от угла
В итоге получается зависимость между временем движения машины от одного положения до другого и углом поворота ведущего звена между этими положениями Для получения закона движения ведущего звена (звена приведения) в форме зависимости
|
|||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.67.8 (0.009 с.) |

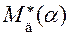 – приведённый момент движущих сил в функции угла поворота кривошипа (рис. 6.6, а);
– приведённый момент движущих сил в функции угла поворота кривошипа (рис. 6.6, а);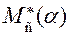 – приведённый момент сил сопротивления в функции угла поворота кривошипа (рис. 6.6, а);
– приведённый момент сил сопротивления в функции угла поворота кривошипа (рис. 6.6, а);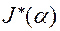 – приведённый момент инерции механизмов машины (рис. 6.6, б);
– приведённый момент инерции механизмов машины (рис. 6.6, б);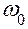 = 0 – значение угловой скорости ведущего звена в начальном положении.
= 0 – значение угловой скорости ведущего звена в начальном положении.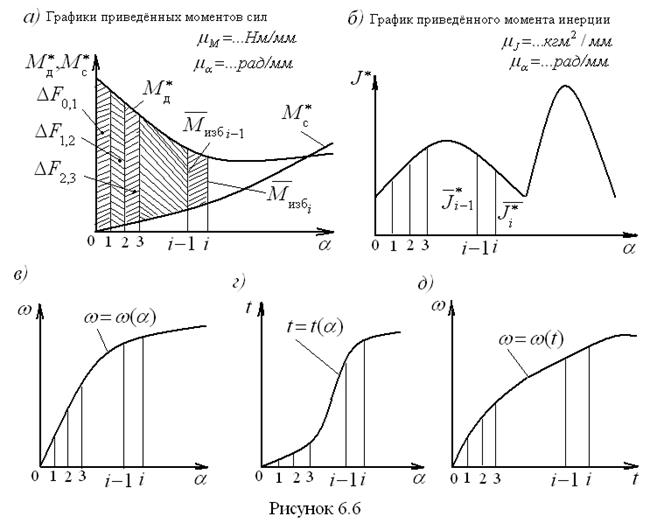 Для исследования используется уравнение динамики в интегральной форме в виде
Для исследования используется уравнение динамики в интегральной форме в виде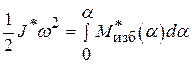 .
.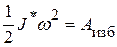 . Решим данное уравнение относительно
. Решим данное уравнение относительно  :
: 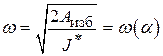 . Обратим внимание на то, что угловая скорость здесь получается как функция от
. Обратим внимание на то, что угловая скорость здесь получается как функция от 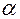 . Это связано с тем, что все составляющие расчётной формулы также зависят от
. Это связано с тем, что все составляющие расчётной формулы также зависят от 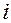 :
: 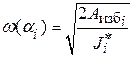 , где
, где 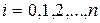 , причём, количество расчётных точек
, причём, количество расчётных точек  можно выбрать любым, но с таким расчётом, чтобы оно заведомо охватывало весь период пуска машины.
можно выбрать любым, но с таким расчётом, чтобы оно заведомо охватывало весь период пуска машины.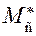 в эту область для удобства дальнейших действий.
в эту область для удобства дальнейших действий.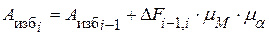 ,
, 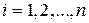 ,
,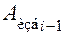 – избыточная работа, выполненная от начального до
– избыточная работа, выполненная от начального до 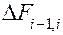 – добавочная площадка между i – 1-м и i -м положениями. Так как на малом участке кривую можно заменить отрезком прямой, то указанные фигуры можно рассматривать как трапеции. Поэтому формула для расчёта площадей запишется так:
– добавочная площадка между i – 1-м и i -м положениями. Так как на малом участке кривую можно заменить отрезком прямой, то указанные фигуры можно рассматривать как трапеции. Поэтому формула для расчёта площадей запишется так: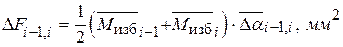 .
.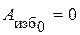 , так как все площадки в нулевом положении равны нулю. Это соответствует моменту начала движения машины.
, так как все площадки в нулевом положении равны нулю. Это соответствует моменту начала движения машины.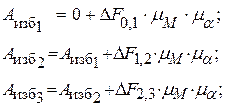
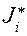 , находим значение угловой скорости в данном, i- м положении. Результаты расчётов угловой скорости представим в виде графика (рис. 6.6, в).
, находим значение угловой скорости в данном, i- м положении. Результаты расчётов угловой скорости представим в виде графика (рис. 6.6, в).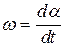 , откуда
, откуда 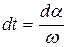 . Проинтегрируем это выражение в пределах каждого из интервалов
. Проинтегрируем это выражение в пределах каждого из интервалов 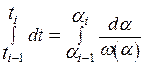 . Вычисление интеграла правой части – задача непростая из-за сложности функции в знаменателе. Поэтому целесообразно воспользоваться приближённой методикой, заключающейся в замене бесконечно малого приращения угла
. Вычисление интеграла правой части – задача непростая из-за сложности функции в знаменателе. Поэтому целесообразно воспользоваться приближённой методикой, заключающейся в замене бесконечно малого приращения угла 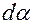 конечной величиной
конечной величиной 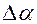 . Если поделить её на среднюю угловую скорость на интервале, то получится искомое время, то есть
. Если поделить её на среднюю угловую скорость на интервале, то получится искомое время, то есть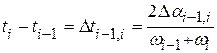 .
.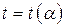 . Эту зависимость представим в виде графика (рис. 6.6, г).
. Эту зависимость представим в виде графика (рис. 6.6, г).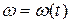 (рис. 6.6, д) теперь достаточно из двух последних графиков (рис. 6.6, в и 6.6, г) исключить параметр
(рис. 6.6, д) теперь достаточно из двух последних графиков (рис. 6.6, в и 6.6, г) исключить параметр 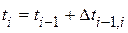 . Дифференцирование по времени полученной в виде графика функции даст новую функцию
. Дифференцирование по времени полученной в виде графика функции даст новую функцию 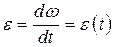 – функцию зависимости углового ускорения звена приведения от времени.
– функцию зависимости углового ускорения звена приведения от времени.


