
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
На работоспособность кулачкового механизмаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Углом давления в кулачковом механизме называется угол между силой, действующей со стороны кулачка на толкатель, и абсолютной скоростью толкателя (или скоростью центра ролика). Так как сила
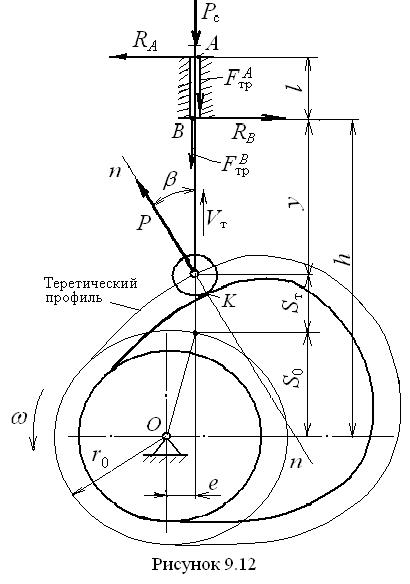
Выясним, как влияет угол давления на возможность передачи усилий кулачковым механизмом. Вследствие зазоров в поступательной кинематической паре под действием силы Сначала необходимо определить реакции Далее, составляем уравнение равновесия в форме моментов сил, действующих на толкатель, относительно точки A:
Записываем уравнение равновесия в форме суммы сил, действующих на толкатель в вертикальном направлении. При этом считаем положительными силы, помогающие движению толкателя, и отрицательными – препятствующие движению. Получаем
Решение данного уравнения относительно
После преобразования суммы в скобках можно записать
При определённом соотношении величин, стоящих в знаменателе, он может обратиться в ноль, то есть будет иметь место равенство
Тогда движущая сила Заменив в последнем равенстве
Вылет толкателя
Из полученного выражения видно, что, чем меньше его правая часть, тем больше критический угол давления. При большем значении критического угла давления механизм имеет больший диапазон возможностей с точки зрения отсутствия заклинивания. Это возможно, в свою очередь: – при уменьшении коэффициента трения – при увеличении длины направляющих – при уменьшении – при увеличении радиуса кулачка Что касается перемещения толкателя При проектировании кулачкового механизма используется так называемый допустимый угол давления Связь между углом давления и геометро-кинематическими Характеристиками механизма
Возьмём кулачковый механизм с поступательно движущимся толкателем, оканчивающимся остриём (рис. 9.13). В таком механизме теоретический и рабочий профили совпадают. Пусть ось толкателя располагается вертикально. Проведём межосевую линию O 1 O 2, имея в виду, что центр вращения толкателя находится в бесконечности, так как толкатель движется поступательно. Затем в точке касания K профиля кулачка с толкателем проведём нормаль
По этой формуле при заданных
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 910; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

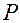 действия кулачка на толкатель направлена вдоль нормали в точке контакта толкателя и кулачка, то угол давления
действия кулачка на толкатель направлена вдоль нормали в точке контакта толкателя и кулачка, то угол давления 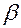 измеряется между осью толкателя, вдоль которой направлена его скорость
измеряется между осью толкателя, вдоль которой направлена его скорость 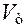 , и указанной нормалью (рис. 9.12).
, и указанной нормалью (рис. 9.12).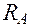 , действующая перпендикулярно направляющим справа налево, и реакция
, действующая перпендикулярно направляющим справа налево, и реакция 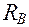 , действующая слева направо также перпендикулярно направляющим. Под действием этих реакций в точках A и B возникают силы трения
, действующая слева направо также перпендикулярно направляющим. Под действием этих реакций в точках A и B возникают силы трения 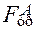 и
и 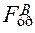 , действующие навстречу движению толкателя, то есть в данном случае вниз. Под действием всех этих сил толкатель находится в равновесии.
, действующие навстречу движению толкателя, то есть в данном случае вниз. Под действием всех этих сил толкатель находится в равновесии.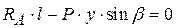 , где
, где 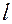 – длина направляющих,
– длина направляющих,  – вылет толкателя (расстояние от нижнего края направляющих до центра ролика. Из уравнения находим
– вылет толкателя (расстояние от нижнего края направляющих до центра ролика. Из уравнения находим 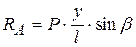 . Сила трения в точке A
. Сила трения в точке A 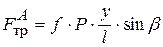 (здесь
(здесь 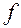 – коэффициент трения в направляющих).
– коэффициент трения в направляющих).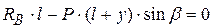 , из которого определяем
, из которого определяем 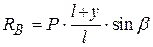 . Сила трения в точке B получится, как
. Сила трения в точке B получится, как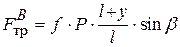 .
.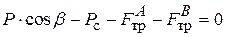 . Подставляя сюда выражения для сил трения, находим
. Подставляя сюда выражения для сил трения, находим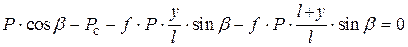 .
.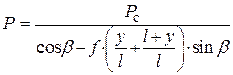 .
.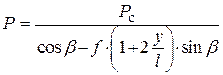 .
.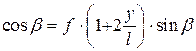 .
.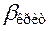 .
.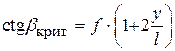 .
.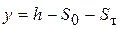 , где
, где 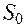 можно записать через радиус основной окружности теоретического профиля
можно записать через радиус основной окружности теоретического профиля 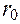 и эксцентриситет
и эксцентриситет 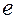 , то есть
, то есть 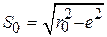 ,
,  – расстояние между нижней плоскостью направляющих и центром кулачка O,
– расстояние между нижней плоскостью направляющих и центром кулачка O, 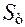 – текущее значение перемещения толкателя. С учётом этого
– текущее значение перемещения толкателя. С учётом этого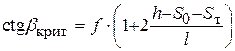 .
.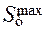 . С изменением величины перемещения изменяется критический угол давления. Наиболее опасным для заклинивания является нулевое значение
. С изменением величины перемещения изменяется критический угол давления. Наиболее опасным для заклинивания является нулевое значение 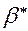 , существенно меньший критического. В фазе удаления допустимый угол давления составляет величину
, существенно меньший критического. В фазе удаления допустимый угол давления составляет величину 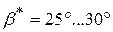 в схеме с поступательно движущимся толкателем и
в схеме с поступательно движущимся толкателем и 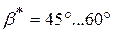 в схеме с качающимся толкателем. В фазе приближения
в схеме с качающимся толкателем. В фазе приближения 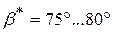 для обеих схем.
для обеих схем.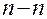 и отметим точку П её пересечения с межосевой линией, являющуюся полюсом зацепления.
и отметим точку П её пересечения с межосевой линией, являющуюся полюсом зацепления.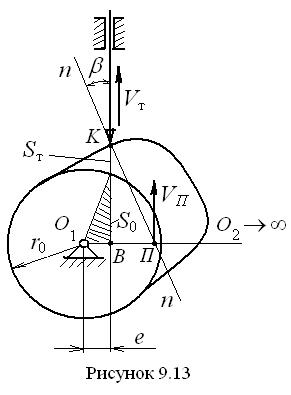 В полюсе зацепления скорости звеньев одинаковы и равны
В полюсе зацепления скорости звеньев одинаковы и равны 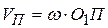 . Отсюда получаем
. Отсюда получаем 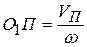 . При поступательном движении звена все его точки, в
. При поступательном движении звена все его точки, в 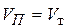 . Следовательно,
. Следовательно, 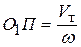 . Данное отношение, как известно, является аналогом скорости
. Данное отношение, как известно, является аналогом скорости 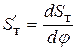 , поэтому
, поэтому 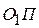 также является аналогом скорости. Из прямоугольного треугольника KBП выразим тангенс угла давления
также является аналогом скорости. Из прямоугольного треугольника KBП выразим тангенс угла давления 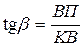 . Из рис. 9.13 видим, что
. Из рис. 9.13 видим, что 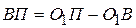 , или
, или 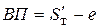 , а
, а 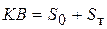 , где выраженное из заштрихованного прямоугольного треугольника
, где выраженное из заштрихованного прямоугольного треугольника 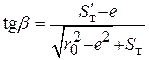 .
.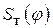 и
и 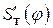 легко определяется угол давления в любом положении механизма. В этом заключается аналитическое решение задачи определения угла давления в кулачковом механизме.
легко определяется угол давления в любом положении механизма. В этом заключается аналитическое решение задачи определения угла давления в кулачковом механизме.


