Кинематика кулачковых механизмов
Похожие статьи вашей тематики
4.1 Схемы и определения
В отличие от рычажных, кулачковые механизмы позволяют сообщить выходному звену практически любой закон движения, в частности, продолжительную остановку, чего не может делать ни один рычажный механизм.
Недостаток кулачковых механизмов состоит в низкой нагрузочной способности пары кулачок-ролик, или кулачок-толкатель, если нет ролика. Недостаток объясняется малой площадью пятна контакта элементов этой пары.
Наиболее распространённые схемы плоских кулачковых механизмов изображены на рис. 4.1.

Рис. 4.1. Распространённые схемы плоских кулачковых механизмов
На всех схемах звенья имеют следующие наименования: 1 – кулачок; 2 – толкатель; 3 – ролик. Пружина 4 звеном не считается, она рассматривается как элемент, обеспечивающий так называемое силовое замыкание высшей пары.
Чем больше скорость вращения кулачка, тем сильнее должна быть пружина и тем выше дополнительная нагрузка на все кинематические пары. Чтобы избавиться от пружины, применяют схемы с геометрическим замыканием (рис. 4.1, г, д).
Представленные схемы отличаются только типом толкателя. В схеме а толкатель стержневой, в схеме б – коромысловый, в схеме в – тарельчатый. Коромысловый толкатель называют коротко коромыслом. Хотя коромысловый толкатель тоже стержневой, путаницы не возникает, т. к. у него есть собственное название.
Смещение  толкателя в схеме а называется эксцентриситетом. При вращении кулачка ось толкателя постоянно касается окружности радиуса толкателя в схеме а называется эксцентриситетом. При вращении кулачка ось толкателя постоянно касается окружности радиуса  , называемой окружностью эксцентриситета (ОЭ). Эксцентриситет может быть равен нулю, и тогда механизм называется центральным. Если , называемой окружностью эксцентриситета (ОЭ). Эксцентриситет может быть равен нулю, и тогда механизм называется центральным. Если 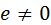 , то механизм называется нецентральным или дезаксиальным. , то механизм называется нецентральным или дезаксиальным.
В механизмах с роликом различают действительный профиль (ДП) и центровой профиль (ЦП) кулачка. Центровойпрофиль – это кривая, которую описывает центр ролика при обкате его по действительному профилю. В плоских механизмах кулачок представляет собой некруглый диск с одним или несколькими горбами, возвышающимися над некоторой базовой окружностью, называемой начальной. Начальная окружность (НО) существует как у действительного, так и у центрового профиля, для теории важна последняя, её радиус 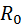 называется начальным. называется начальным.
В общем случае в работе любого кулачкового механизма c одногорбовым кулачком можно выделить четыре фазы движения толкателя: фазу подъёма; верхнего выстоя; опускания; нижнего выстоя.
При вращении кулачка против часовой стрелки (см. рис. 4.1, а) названным фазам соответствуют участки 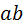 , , 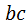 , , 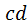 , , 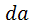 центрового профиля кулачка. Участки выстоя – центрового профиля кулачка. Участки выстоя –  , , 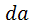 очерчены дугами окружностей, проведёнными из центра вращения кулачка. очерчены дугами окружностей, проведёнными из центра вращения кулачка.
Анализ механизма первой схемы
Кинематические диаграммы
Первой считается схема, изображённая на рис. 4.1, а. Первоочередным для любого механизма является кинематический анализ. Применительно к кулачковому механизму он состоит в определении положения, скорости и ускорения толкателя по положению, скорости и ускорению кулачка. При графическом решении задачи схему вычерчивают в некотором масштабе. Для упрощения решения действительный профиль кулачка заменяют центровым ЦП и удаляют из схемы ролик (рис. 4.2, а).
Отсчёт координат кулачка и толкателя ведут от начала фазы подъёма. Сплошной линией изображено начальное положение центрового профиля ЦП кулачка, пунктиром – положение после поворота кулачка на угол 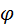 . Функцией положения является зависимость . Функцией положения является зависимость 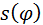 . Очевидный способ установления этой зависимости состоит в построении профиля кулачка при разных значениях угла . Очевидный способ установления этой зависимости состоит в построении профиля кулачка при разных значениях угла 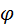 и последующем измерении расстояния и последующем измерении расстояния 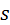 . Однако многократное построение кривой, по которой очерчен кулачок, трудоёмко. Чтобы преодолеть это затруднение, механизм переставляют на кулачок, и вместо поворота кулачка, на тот же угол, но в обратную сторону, поворачивают стойку вместе с толкателем . Однако многократное построение кривой, по которой очерчен кулачок, трудоёмко. Чтобы преодолеть это затруднение, механизм переставляют на кулачок, и вместо поворота кулачка, на тот же угол, но в обратную сторону, поворачивают стойку вместе с толкателем
(рис. 4.2, б). Этот приём называется обращением движения. Отрезок 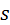 оси толкателя, отсекаемый начальной окружностью и центровым профилем кулачка, есть искомая координата толкателя. оси толкателя, отсекаемый начальной окружностью и центровым профилем кулачка, есть искомая координата толкателя.
Рис. 4.2. Определение координаты толкателя непосредственно – а
и методом обращения движения – б
Повторяя рассмотренные построения для других значений угла 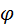 , находят соответствующие значения , находят соответствующие значения 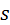 и по ним строят график зависимости и по ним строят график зависимости 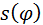 . Двукратным дифференцированием этой зависимости получают графики . Двукратным дифференцированием этой зависимости получают графики 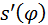 и и 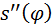 (см. раздел 3.3). Скорость и ускорение толкателя определяют по формулам (3.7), (3.8). (см. раздел 3.3). Скорость и ускорение толкателя определяют по формулам (3.7), (3.8).
Угол давления
Вообще – это угол 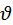 между силой между силой 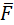 и скоростью и скоростью 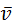 точки приложения силы. В кулачковых механизмах речь идет о силе точки приложения силы. В кулачковых механизмах речь идет о силе 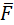 , действующей со стороны кулачка на толкатель (рис. 4.3). , действующей со стороны кулачка на толкатель (рис. 4.3).
| Рис. 4.3. Угол давления J
| Чтобы не усложнять вопрос, угол давления определяют без учёта сил трения. При таком допущении сила 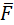 действует по нормали действует по нормали
n – n к профилю кулачка – действительному и центровому. На фазе подъёма (вид а) угол давления положительный, на фазе опускания(вид б) отрицательный.
Почему важен угол давления? Выше отмечалось, что закон движения толкателя определяют отрезки 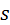 , заключённые между начальной окружностью и профилем кулачка (см. рис. 4.2). Это означает, что один и тот же закон движения может быть обеспечен при разных начальных радиусах , заключённые между начальной окружностью и профилем кулачка (см. рис. 4.2). Это означает, что один и тот же закон движения может быть обеспечен при разных начальных радиусах 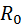 и разных эксцентриситетах и разных эксцентриситетах  . Естественно стремление к уменьшению радиуса . Естественно стремление к уменьшению радиуса 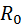 . Но, как видно по рис. 4.4, при этом возрастают углы давления (сравните . Но, как видно по рис. 4.4, при этом возрастают углы давления (сравните 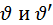 ). ).
| Рис. 4.4. Влияние начального радиуса на угол давления
| Одновремённо возрастает сила 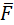 (сравните (сравните 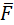 и и 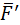 ), необходимая для преодоления одного и того же полезного сопротивления. Это плохо, т. к. увеличивает контактные напряжения между кулачком и роликом. Кроме того, возрастает вредная составляющая ), необходимая для преодоления одного и того же полезного сопротивления. Это плохо, т. к. увеличивает контактные напряжения между кулачком и роликом. Кроме того, возрастает вредная составляющая 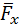 , увеличивающая силы трения в направляющей толкателя. Как следствие, снижается КПД механизма. , увеличивающая силы трения в направляющей толкателя. Как следствие, снижается КПД механизма.
Существует также такое значение 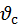 угла давления, по достижении которого толкатель останавливается и не может сдвинуться с места даже при отсутствии какого-либо полезного сопротивления. Такое явление называется самоторможением, а угла давления, по достижении которого толкатель останавливается и не может сдвинуться с места даже при отсутствии какого-либо полезного сопротивления. Такое явление называется самоторможением, а 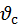 – углом самоторможения. Всё это и объясняет, почему важен угол давления. – углом самоторможения. Всё это и объясняет, почему важен угол давления.
На углы давления влияет не только начальный радиус, но и эксцентриситет 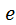 . На рис. 4.5изображён механизм без эксцентриситета – вид а и с эксцентриситетом – вид б. . На рис. 4.5изображён механизм без эксцентриситета – вид а и с эксцентриситетом – вид б.
Рис. 4.5. Влияние эксцентриситета на углы давления
Оба кулачка имеют один и тот же начальный радиус и сообщают толкателю один и тот же закон движения. Введение эксцентриситета равносильно развороту отрезков  , , 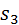 и им подобным вокруг своих оснований на один и тот же угол. В результате разворота профиль кулачка деформируется, углы давления на фазе подъёма уменьшаются (сравните и им подобным вокруг своих оснований на один и тот же угол. В результате разворота профиль кулачка деформируется, углы давления на фазе подъёма уменьшаются (сравните 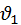 и и 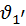 ),на фазе опускания увеличиваются (сравните ),на фазе опускания увеличиваются (сравните 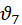 и и 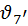 ). Уменьшение желательно, увеличение нежелательно, но для фазы опускания допустимо, т. к. это фаза холостого хода. Таким образом, эксцентриситет только перераспределяет углы давления. ). Уменьшение желательно, увеличение нежелательно, но для фазы опускания допустимо, т. к. это фаза холостого хода. Таким образом, эксцентриситет только перераспределяет углы давления.
|


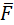 действует по нормали
действует по нормали 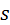 , заключённые между начальной окружностью и профилем кулачка (см. рис. 4.2). Это означает, что один и тот же закон движения может быть обеспечен при разных начальных радиусах
, заключённые между начальной окружностью и профилем кулачка (см. рис. 4.2). Это означает, что один и тот же закон движения может быть обеспечен при разных начальных радиусах 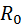 и разных эксцентриситетах
и разных эксцентриситетах  . Естественно стремление к уменьшению радиуса
. Естественно стремление к уменьшению радиуса 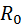 . Но, как видно по рис. 4.4, при этом возрастают углы давления (сравните
. Но, как видно по рис. 4.4, при этом возрастают углы давления (сравните 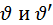 ).
).
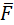 (сравните
(сравните 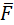 и
и 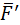 ), необходимая для преодоления одного и того же полезного сопротивления. Это плохо, т. к. увеличивает контактные напряжения между кулачком и роликом. Кроме того, возрастает вредная составляющая
), необходимая для преодоления одного и того же полезного сопротивления. Это плохо, т. к. увеличивает контактные напряжения между кулачком и роликом. Кроме того, возрастает вредная составляющая 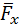 , увеличивающая силы трения в направляющей толкателя. Как следствие, снижается КПД механизма.
, увеличивающая силы трения в направляющей толкателя. Как следствие, снижается КПД механизма.

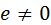 , то механизм называется нецентральным или дезаксиальным.
, то механизм называется нецентральным или дезаксиальным.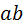 ,
, 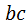 ,
, 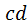 ,
, 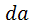 центрового профиля кулачка. Участки выстоя –
центрового профиля кулачка. Участки выстоя –  ,
, 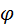 . Функцией положения является зависимость
. Функцией положения является зависимость 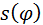 . Очевидный способ установления этой зависимости состоит в построении профиля кулачка при разных значениях угла
. Очевидный способ установления этой зависимости состоит в построении профиля кулачка при разных значениях угла 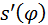 и
и 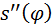 (см. раздел 3.3). Скорость и ускорение толкателя определяют по формулам (3.7), (3.8).
(см. раздел 3.3). Скорость и ускорение толкателя определяют по формулам (3.7), (3.8).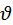 между силой
между силой 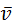 точки приложения силы. В кулачковых механизмах речь идет о силе
точки приложения силы. В кулачковых механизмах речь идет о силе 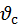 угла давления, по достижении которого толкатель останавливается и не может сдвинуться с места даже при отсутствии какого-либо полезного сопротивления. Такое явление называется самоторможением, а
угла давления, по достижении которого толкатель останавливается и не может сдвинуться с места даже при отсутствии какого-либо полезного сопротивления. Такое явление называется самоторможением, а 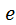 . На рис. 4.5изображён механизм без эксцентриситета – вид а и с эксцентриситетом – вид б.
. На рис. 4.5изображён механизм без эксцентриситета – вид а и с эксцентриситетом – вид б. ,
, 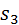 и им подобным вокруг своих оснований на один и тот же угол. В результате разворота профиль кулачка деформируется, углы давления на фазе подъёма уменьшаются (сравните
и им подобным вокруг своих оснований на один и тот же угол. В результате разворота профиль кулачка деформируется, углы давления на фазе подъёма уменьшаются (сравните 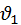 и
и 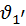 ),на фазе опускания увеличиваются (сравните
),на фазе опускания увеличиваются (сравните 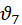 и
и 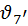 ). Уменьшение желательно, увеличение нежелательно, но для фазы опускания допустимо, т. к. это фаза холостого хода. Таким образом, эксцентриситет только перераспределяет углы давления.
). Уменьшение желательно, увеличение нежелательно, но для фазы опускания допустимо, т. к. это фаза холостого хода. Таким образом, эксцентриситет только перераспределяет углы давления.


