
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика рычажных механизмовСодержание книги
Поиск на нашем сайте
В этом разделе будут рассмотрены только плоские механизмы. Ёмкое слово «кинематика», стоящее в заголовке, означает: кинематический анализ и синтез. Кинематический анализ состоит в определении положений, скоростей и ускорений отдельных точек и звеньев в целом. Ниже рассматриваются графические методы кинематического анализа. Определение положений Дана схема механизма, вычерченная в определённом масштабе (рис. 3.1, а). Требуется построить эту схему при некотором новом значении Построение схемы начинают с изображения звеньев 0, 1 под углом Звено 1 с задаваемым положением называют начальным. Соответственно и весь механизм 0, 1, построенный на данном этапе, называют начальным механизмом, хотя это всего лишь зародыш механизма. Чтобы решить, какие звенья пристроить к начальному механизму в первую очередь, воображают, что механизм собирается из разрозненных звеньев, причём начальный механизм уже собран и угол Звенья 2, 3, взятые с исходной картины (рис. 3.1, а), присоединяют по отдельности к телу Ф1. У звена 2 берут пока только сторону Траектории с2 – с2 и с3 – с3 представляют собой геометрические места точек С 2 и С 3, поэтому метод определения положения точки С называют методом геометрических мест. Этот метод называют также методом засечек. Положение точки E и других сторон звена 2 (рис. 3.1, г) находят, снимая размеры этого звена с рис. 3.1, а. На этом построение цепи 2, 3 завершено. После цепи 2, 3 становится возможным определение положения цепи 4, 5 (рис. 3.1, д). Для этого всё ранее построенное превращают в одно твёрдое тело Ф2. Звенья 4, 5 присоединяют по отдельности к телу Ф2. Вращая звено 4 вокруг точки E и перемещая ползун 5 по направляющей, строят траектории f4 – f4 и f5 – f5 точек F 4, F 5. На пересечении траекторий находят положение шарнира F. Соединяя точки E и F, получают положение звена 4. Положение звена 5 определяет точка F. На этом задача определения положений всех звеньев решена. Подытоживая, получают следующий порядок построения схемы: 0, 1 + 2, 3 + 4, 5.
Рис. 3.1. Построение схемы механизма Если схему строить по заданному положению звена 3, то порядок построения будет следующим: 0, 3 + 1, 2 + 4, 5 (см. рис. 3.1, а). При этом в методике решения задачи не будет ничего нового. При построении схемы по заданному положению звена 5 или, иначе, по координате Звено 5 устанавливают на заданное расстояние Если для каждого момента времени определимо положение цепи, то определимы скорости, ускорения и любые другие характеристики движения. На этом основании ц е пи, положение которых определимо на каждом этапе построения схемы, называются кинематически определимыми. Рис. 3.2. Построение схемы механизма Первые закономерности строения кинематически определимых цепей звеньев нашёл в начале прошлого столетия петербургский профессор Леонид Владимирович Ассур (1878–1920). В его честь кинематически определимые цепи назвали цепями или группами Ассура. Группы Ассура Чтобы выявить количественные характеристики своих групп, Ассур предложил рассматривать их как надстоечную часть особого механизма, стойкой которого является предшествующий механизм, превращённый в одно твёрдое тело. Для цепи 2, 3
У надстоечной части число степеней свободы
Двумерные модели рычажных механизмов содержат только вращательные и поступательные кинематические пары. Все они двусвязные (см. рис. 2.8), поэтому общее число связей представимо в виде
Таким должно быть соотношение между числом звеньев и числом двусвязных кинематических пар в группах Ассура. Последнему уравнению удовлетворяют лишь чётные
Чисто шарнирные варианты или, иначе, основные модификации двузвенных и четырёхзвенных групп, построенных в соответствии с таблицей, показаны на рис. 3.3. Рис. 3.3. Основные модификации двухзвенных За штрихпунктирной линией скрыт механизм, предшествующий присоединению группы Ассура. Группы а, б, в отнесены ко второму, третьему и четвёртому классам соответственно. Прочие модификации групп Ассура любого класса получают последовательной заменой вращательных пар поступательными. Последняя модификация (рис. 3.4, е) не обладает определённостью положения относительно предшествующего механизма (стрелки показывают направление возможного движения звеньев). Это вырожденная группа Ассура. При определённой геометрии вырожденной может оказаться любая другая группа, но последняя остаётся вырожденной всегда. Механизмы, содержащие вырожденные группы Ассура, в данном курсе не рассматриваются. Рис. 3.4. Все модификации двухзвенной группы Ассура На рис. 3.5 показаны некоторые модификации трёхповодковой группы Ассура. Рис. 3.5. Некоторые модификации четырёхзвенной группы Ассура Во всех модификациях звено 4 – базовое, 1, 2, 3 – поводки. Нет необходимости запоминать все модификации групп Ассура, достаточно помнить только основные, показанные на рис. 3.3. Методы определения скоростей и ускорений в часто встречающихся группах Ассура хорошо разработаны, поэтому после разложения механизма на группы Ассура его кинематический анализ перестаёт быть проблемой. Чтобы разложить на группы Ассура зубчатый или кулачковый механизм, пары с точечным касанием – высшие – заменяют кинематически эквивалентными цепями, содержащими тольконизшие пары – вращательные и поступательные. Замена высших пар Чтобы произвести замену в зубчатом механизме (рис. 3.6, а), через точку касания Если один из элементов высшей пары прямолинейный (рис. 3.6, б), то шарнир
Рис. 3.6. Замена высших пар Заменяющий механизм кинематически эквивалентен заменяемому до производных второго порядка. Это значит, что с его помощью можно правильно определять только скорости и ускорения. Планы скоростей и ускорений Универсальным методом решения указанной в заглавии задачи является план скоростей и план ускорений, известный из курса теоретической механики. Вклад теории механизмов состоит в указании стратегии решения этой задачи: как и положения звеньев, скорости и ускорения определяют переходя от одной группы Ассура к другой. При этом начальным считают звено с заданной скоростью и ускорением. Обычно это то же звено, что и в задаче о положениях.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 537; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.26 (0.008 с.) |

 угла
угла 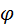 , характеризующего положение звена 1.
, характеризующего положение звена 1. . Вращая звенья вокруг точек В и D, получают траектории с2 – с2 и с3 – с3 их свободных концов. На пересечении траекторий отмечают точку С. Точку С соединяют с точками В и D, в результате находят положение звена 3 и одной стороны звена 2.
. Вращая звенья вокруг точек В и D, получают траектории с2 – с2 и с3 – с3 их свободных концов. На пересечении траекторий отмечают точку С. Точку С соединяют с точками В и D, в результате находят положение звена 3 и одной стороны звена 2. (рис. 3.2, а), не удастся найти ни одной двухзвенной цепи, положение которой было бы определимо. Определить положение можно лишь вовлекая в построения все оставшиеся звенья. Это делается следующим образом.
(рис. 3.2, а), не удастся найти ни одной двухзвенной цепи, положение которой было бы определимо. Определить положение можно лишь вовлекая в построения все оставшиеся звенья. Это делается следующим образом. (рис. 3.2, б). Звено 2 (треугольное) отсоединяют от звеньев 1, 3, 4. Изображают траектории b1 – b1, c3 – c3, e4 – e4 освободившихся концов этих звеньев. Звено 2 помещают какими-либо двумя вершинами на свои траектории, например c3 – c3 и e4 – e4, и, скользя по ним, получают траекторию b2 – b2 третьей вершины. На пересечении траекторий b1 – b1 и b2 – b2 располагают шарнир В. Соединяя шарниры A и B, находят положение звена 1. По положению звена 1 определяют положение звеньев 2, 3 и 4, 5. Это делают уже известным способом, рассмотренным выше. В цифровом виде порядок построения имеет вид: 0, 5 + 1, 2, 3, 4.
(рис. 3.2, б). Звено 2 (треугольное) отсоединяют от звеньев 1, 3, 4. Изображают траектории b1 – b1, c3 – c3, e4 – e4 освободившихся концов этих звеньев. Звено 2 помещают какими-либо двумя вершинами на свои траектории, например c3 – c3 и e4 – e4, и, скользя по ним, получают траекторию b2 – b2 третьей вершины. На пересечении траекторий b1 – b1 и b2 – b2 располагают шарнир В. Соединяя шарниры A и B, находят положение звена 1. По положению звена 1 определяют положение звеньев 2, 3 и 4, 5. Это делают уже известным способом, рассмотренным выше. В цифровом виде порядок построения имеет вид: 0, 5 + 1, 2, 3, 4. . Подставляя это число в структурную формулу двумерной модели механизма (
. Подставляя это число в структурную формулу двумерной модели механизма (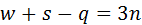 ) и ограничиваясь механизмами, не содержащими избыточных связей (у них
) и ограничиваясь механизмами, не содержащими избыточных связей (у них 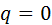 ), Ассур получил:
), Ассур получил: .
. , где
, где 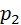 – количество кинематических пар с двумя связями. С учётом всех допущений получают:
– количество кинематических пар с двумя связями. С учётом всех допущений получают:  . Отсюда
. Отсюда .
.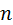 , т. к.
, т. к. 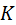 профилей зубьев (элементов высшей пары) проводят к ним нормаль n – n. Отмечают центры кривизны
профилей зубьев (элементов высшей пары) проводят к ним нормаль n – n. Отмечают центры кривизны  ,
,  профилей. Вводят звено 3, соединяя его шарнирно в точках
профилей. Вводят звено 3, соединяя его шарнирно в точках  и
и  – и получают заменяющий механизм
– и получают заменяющий механизм  , не содержащий высших пар.
, не содержащий высших пар.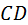 относительно звена 2 превращается в поступательное, направленное вдоль прямолинейного элемента звена 2. На этом основании конец
относительно звена 2 превращается в поступательное, направленное вдоль прямолинейного элемента звена 2. На этом основании конец 



