Исходный производящий контур
Контур назван исходным, т. к. через него определяются параметры производимого колеса. До сих этот контур изображался на всех рисунках упрощённо – в виде регулярной ломаной линии. На самом деле контур отличается небольшими закруглениями по углам (рис. 5.10).
Рис. 5.10. Исходный производящий реечный контур
Параметры контура стандартизованы. Если при стандартизации шаг  производящего контура выбирать из существующего в машиностроении ряда предпочтительных чисел, а там числа, прежде всего, целые, то радиус делительной окружности производимого колеса будет выражаться иррациональным числом. Это видно по формуле (5.7), где производящего контура выбирать из существующего в машиностроении ряда предпочтительных чисел, а там числа, прежде всего, целые, то радиус делительной окружности производимого колеса будет выражаться иррациональным числом. Это видно по формуле (5.7), где  теперь называется радиусом делительной окружности. Чтобы избежать иррациональности, шаг представили в виде теперь называется радиусом делительной окружности. Чтобы избежать иррациональности, шаг представили в виде
 , (5.8) , (5.8)
где 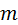 – целое или дробное рациональное число, выражаемое в миллиметрах и называемое модулем производящего контура. После подстановки (5.8) в (5.7) радиус делительной окружности имеет вид: – целое или дробное рациональное число, выражаемое в миллиметрах и называемое модулем производящего контура. После подстановки (5.8) в (5.7) радиус делительной окружности имеет вид:
 . (5.9) . (5.9)
Из формулы (5.8) следует, что 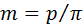 , т. е. модуль равен -й части шага производящего контура. Шаг производящего контура копируется на делительную окружность производимого колеса, копируется и его p -я часть. На этом основании говорят, что колесо имеет такой же модуль, как производящий контур. Размеры контура по высоте определяют через так называемый коэффициент радиального зазора , т. е. модуль равен -й части шага производящего контура. Шаг производящего контура копируется на делительную окружность производимого колеса, копируется и его p -я часть. На этом основании говорят, что колесо имеет такой же модуль, как производящий контур. Размеры контура по высоте определяют через так называемый коэффициент радиального зазора  и коэффициент высоты головки зуба и коэффициент высоты головки зуба 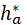 . По стандарту . По стандарту  , ,  . Единственный нелинейный параметр производящего контура – угол профиля . Единственный нелинейный параметр производящего контура – угол профиля 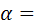 20°. 20°.
Параметры колеса и зацепления
Станочное зацепление
Зацепление изображено на рис. 5.11. Производящая рейка в нём установлена со смещением 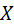 . Это смещение представляют в виде . Это смещение представляют в виде 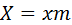 , где , где  – коэффициент смещения, а – коэффициент смещения, а 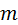 – модуль. Коэффициент смещения, как и само смещение, имеет знак. – модуль. Коэффициент смещения, как и само смещение, имеет знак. 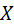 – это абсолютное смещение, – это абсолютное смещение,  – относительное. Соответственно смещению рейки произведённые колёса называются положительными, отрицательными или нулевыми. Из станочного зацепления можно вывести все параметры колеса, кроме радиуса окружности вершин. – относительное. Соответственно смещению рейки произведённые колёса называются положительными, отрицательными или нулевыми. Из станочного зацепления можно вывести все параметры колеса, кроме радиуса окружности вершин.
Радиус 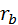 основной окружности.Из основной окружности.Из  следует: следует:
 . .
Радиус 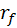 окружности впадин. окружности впадин. | Рис. 5.11. Станочное зацепление
|  или или
 . .
Толщина 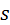 зуба по делительной окружности. зуба по делительной окружности.
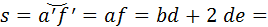
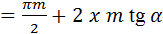 или или
 . .
Минимальное число зубьев из условия неподрезания.
Подрез – это выемка на ножке зуба, появляющаяся вследствие интерференции в станочном зацеплении. Интерференция, как известно, возникает тогда, когда активная линия зацепления зубчатых звеньев выходит за какую-либо границу всей линии зацепления. Пусть одной и той же производящей рейкой, установленной без смещения, производятся три колеса с разными числами зубьев, причём  (рис. 5.12). (рис. 5.12).
Рис. 5.12. Подрез ножки зуба с уменьшением числа зубьев:
а – подреза нет; б – колесо на грани подреза; в – подрез есть
На всех трёх видах приняты следующие обозначения: 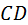 – вся линия зацепления (точка – вся линия зацепления (точка  находится в бесконечности), находится в бесконечности), 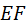 – активная линия зацепления. Точка – активная линия зацепления. Точка 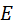 определена без учёта скруглённой части зуба рейки, т. к. эта часть в образовании эвольвенты не участвует и, следовательно, её не подрезает. определена без учёта скруглённой части зуба рейки, т. к. эта часть в образовании эвольвенты не участвует и, следовательно, её не подрезает.
В случае, показанном на виде а, подрез колесу не угрожает, т. к. активная линия зацепления не выходит за границу  всей линии зацепления. В случае б границы всей линии зацепления. В случае б границы  , , 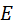 линий зацепления совпадают и колесо находится на грани подреза. В случае в активная линия зацепления вышла за границу всей линии зацепления и ножка зуба будет подрезана. Подрезом считается только такая выемка в основании зуба, которая захватывает эвольвенту. Поэтому не всякое видимое поднутрение в основании зуба считается подрезом. линий зацепления совпадают и колесо находится на грани подреза. В случае в активная линия зацепления вышла за границу всей линии зацепления и ножка зуба будет подрезана. Подрезом считается только такая выемка в основании зуба, которая захватывает эвольвенту. Поэтому не всякое видимое поднутрение в основании зуба считается подрезом.
Число зубьев колеса на виде б обозначают через  . Это число наименьшее из условия неподрезания. Из рисунка следует: . Это число наименьшее из условия неподрезания. Из рисунка следует: 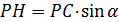 ; ;  . После подстановки получают: . После подстановки получают:  . Выражая отрезки через модуль, находят, что . Выражая отрезки через модуль, находят, что 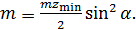 Отсюда Отсюда 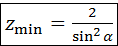 . При . При 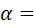 20° 20°  . .
Минимальный коэффициент смещения из условия неподрезания.В случае в колесо получается с подрезом. Чтобы его устранить, необходимо сдвинуть рейку от центра колеса как минимум на  . При этом точка . При этом точка 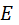 совпадёт с совпадёт с  и возникнет ситуация, показанная на виде б. Таким образом, и возникнет ситуация, показанная на виде б. Таким образом,  – это минимальное смещение, необходимое для устранения подреза. – это минимальное смещение, необходимое для устранения подреза.
 . Смещение . Смещение 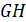 представляют в виде представляют в виде 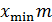 , где , где 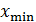 – коэффициент минимального смещения; – коэффициент минимального смещения;  . Из предыдущего известно, что . Из предыдущего известно, что 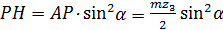 . Возвращаясь в формулу для . Возвращаясь в формулу для 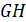 и удаляя индекс при и удаляя индекс при 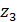 , получают: , получают:  . Отсюда . Отсюда 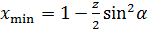 . С учётом формулы для . С учётом формулы для  , а также принимая, что , а также принимая, что  , получают , получают 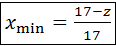 . .
Рабочее зацепление
Угол зацепления. Как отмечено выше, рабочим называется зацепление произведённых колёс друг с другом. Из картины этого зацепления (рис. 5.13) выводят, прежде всего, формулу инволюты угла зацепления. Вывод громоздкий, поэтому приводим формулу в готовом виде:
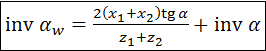 . .
Рис. 5.13. Рабочее зацепление
Величины, входящие в эту формулу, известны. Угол зацепления 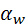 находят по таблице эвольвентной функции. находят по таблице эвольвентной функции.
Межцентровое расстояние. Из рис. 5.13 следует:
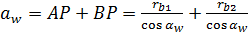 . .
Для любого колеса радиус основной окружности 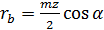 . .
После индексации и подстановок получают:
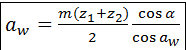 . .
Радиус 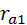 окружности вершин зубьев. Непосредственно из рис. 5.13 следует: окружности вершин зубьев. Непосредственно из рис. 5.13 следует: 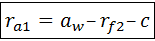 . .
Входящий в формулу радиальный зазор  принимают равным высоте принимают равным высоте 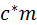 закруглённой части производящего контура, т. е. 0,25 закруглённой части производящего контура, т. е. 0,25 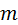 . .
Коэффициент перекрытия.Перекрытием называется такое чередование работы зубьев, при котором каждая следующая пара зубьев входит в зацепление раньше, чем выйдет из него предыдущая.
| Рис. 5.14. Иллюстрация перекрытия
| На рис. 5.14 зубья входят в зацепление в точке 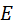 , а выходят в точке , а выходят в точке 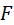 . Пара зубьев, соприкасающихся в точке . Пара зубьев, соприкасающихся в точке 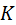 , ещё не дошла до конца активной линии зацепления, а следующая уже вошла , ещё не дошла до конца активной линии зацепления, а следующая уже вошла
в зацепление, следовательно, перекрытие есть. Степень перекрытия оценивают коэффициентом перекрытия 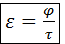 , где , где 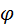 – угол поворота какого-либо из колёс за время зацепления одной пары зубьев; – угол поворота какого-либо из колёс за время зацепления одной пары зубьев;  – угловой шаг того же колеса. Шаг – угловой шаг того же колеса. Шаг  . Перекрытие обеспечивается, если . Перекрытие обеспечивается, если 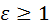 , т. е. , т. е. 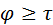 . Для эвольвентного зацепления коэффициент перекрытия может быть определён проще. В радианном измерении . Для эвольвентного зацепления коэффициент перекрытия может быть определён проще. В радианном измерении
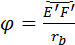 , , 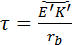 . Дуга . Дуга 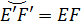 , ,  . После подстановок . После подстановок
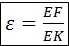 . .
Таким образом, перекрытие обеспечивается, если 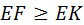 , т. е. активная линия зацепления длиннее шага колеса по той же линии. , т. е. активная линия зацепления длиннее шага колеса по той же линии.
Если  , то в зацеплении постоянно находится только одна пара зубьев, если , то в зацеплении постоянно находится только одна пара зубьев, если 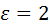 , то – две, и т. д. Если , то – две, и т. д. Если 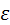 заключено между единицей и двойкой, то в зацеплении поочерёдно находится то одна, то две пары зубьев. заключено между единицей и двойкой, то в зацеплении поочерёдно находится то одна, то две пары зубьев.
Блокирующие контуры
| Рис. 5.15. Блокирующий контур
| Влияние коэффициентов смещения на параметры зацепления труднообозримо, поэтому в помощь расчётчикам созданы справочные материалы. Эти материалы представляют собой систему графиков, ограничивающих выбор коэффициентов смещения, исходя из геометрической безупречности зубчатой передачи. Графики образуют замкнутую область и поэтому называются блокирующими контурами (рис. 5.15).
Каждый контур строится для определённого сочетания чисел зубьев 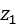 , , 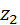 . Осями координат контура являются коэффициенты смещения . Осями координат контура являются коэффициенты смещения 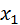 , ,  . Коэффициенты смещения должны соответствовать любой точке, заключенной внутри контура или лежащей на его границе. Такой выбор коэффициентов гарантирует следующие четыре качества зацепления: . Коэффициенты смещения должны соответствовать любой точке, заключенной внутри контура или лежащей на его границе. Такой выбор коэффициентов гарантирует следующие четыре качества зацепления:
1) отсутствие интерференции в рабочем зацеплении (незаклинивание);
2) отсутствие интерференции в станочном зацеплении (неподрезание);
3) толщину зуба при вершине  (незаострение); (незаострение);
4) коэффициент перекрытия 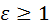 (непрерывность зацепления). (непрерывность зацепления).
Выбор коэффициентов смещения на границе контура даёт зацепление, у которого одно из указанных выше качеств оказывается на пределе допустимого.
|


 или
или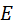 , а выходят в точке
, а выходят в точке 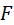 . Пара зубьев, соприкасающихся в точке
. Пара зубьев, соприкасающихся в точке 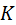 , ещё не дошла до конца активной линии зацепления, а следующая уже вошла
, ещё не дошла до конца активной линии зацепления, а следующая уже вошла 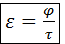 , где
, где 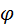 – угол поворота какого-либо из колёс за время зацепления одной пары зубьев;
– угол поворота какого-либо из колёс за время зацепления одной пары зубьев;  – угловой шаг того же колеса. Шаг
– угловой шаг того же колеса. Шаг  . Перекрытие обеспечивается, если
. Перекрытие обеспечивается, если 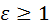 , т. е.
, т. е. 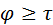 . Для эвольвентного зацепления коэффициент перекрытия может быть определён проще. В радианном измерении
. Для эвольвентного зацепления коэффициент перекрытия может быть определён проще. В радианном измерении

 производящего контура выбирать из существующего в машиностроении ряда предпочтительных чисел, а там числа, прежде всего, целые, то радиус делительной окружности производимого колеса будет выражаться иррациональным числом. Это видно по формуле (5.7), где
производящего контура выбирать из существующего в машиностроении ряда предпочтительных чисел, а там числа, прежде всего, целые, то радиус делительной окружности производимого колеса будет выражаться иррациональным числом. Это видно по формуле (5.7), где  теперь называется радиусом делительной окружности. Чтобы избежать иррациональности, шаг представили в виде
теперь называется радиусом делительной окружности. Чтобы избежать иррациональности, шаг представили в виде , (5.8)
, (5.8)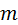 – целое или дробное рациональное число, выражаемое в миллиметрах и называемое модулем производящего контура. После подстановки (5.8) в (5.7) радиус делительной окружности имеет вид:
– целое или дробное рациональное число, выражаемое в миллиметрах и называемое модулем производящего контура. После подстановки (5.8) в (5.7) радиус делительной окружности имеет вид: . (5.9)
. (5.9)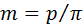 , т. е. модуль равен -й части шага производящего контура. Шаг производящего контура копируется на делительную окружность производимого колеса, копируется и его p -я часть. На этом основании говорят, что колесо имеет такой же модуль, как производящий контур. Размеры контура по высоте определяют через так называемый коэффициент радиального зазора
, т. е. модуль равен -й части шага производящего контура. Шаг производящего контура копируется на делительную окружность производимого колеса, копируется и его p -я часть. На этом основании говорят, что колесо имеет такой же модуль, как производящий контур. Размеры контура по высоте определяют через так называемый коэффициент радиального зазора  и коэффициент высоты головки зуба
и коэффициент высоты головки зуба 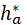 . По стандарту
. По стандарту  ,
,  . Единственный нелинейный параметр производящего контура – угол профиля
. Единственный нелинейный параметр производящего контура – угол профиля 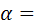 20°.
20°.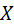 . Это смещение представляют в виде
. Это смещение представляют в виде 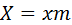 , где
, где  – коэффициент смещения, а
– коэффициент смещения, а 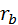 основной окружности.Из
основной окружности.Из  следует:
следует: .
.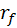 окружности впадин.
окружности впадин.  .
.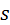 зуба по делительной окружности.
зуба по делительной окружности.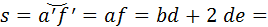
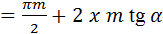 или
или .
. (рис. 5.12).
(рис. 5.12).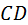 – вся линия зацепления (точка
– вся линия зацепления (точка  находится в бесконечности),
находится в бесконечности), 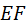 – активная линия зацепления. Точка
– активная линия зацепления. Точка  всей линии зацепления. В случае б границы
всей линии зацепления. В случае б границы  . Это число наименьшее из условия неподрезания. Из рисунка следует:
. Это число наименьшее из условия неподрезания. Из рисунка следует: 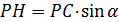 ;
;  . После подстановки получают:
. После подстановки получают:  . Выражая отрезки через модуль, находят, что
. Выражая отрезки через модуль, находят, что 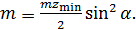 Отсюда
Отсюда 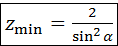 . При
. При 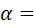 20°
20°  .
. . При этом точка
. При этом точка 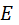 совпадёт с
совпадёт с  . Смещение
. Смещение 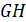 представляют в виде
представляют в виде 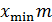 , где
, где 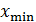 – коэффициент минимального смещения;
– коэффициент минимального смещения;  . Из предыдущего известно, что
. Из предыдущего известно, что 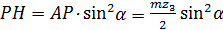 . Возвращаясь в формулу для
. Возвращаясь в формулу для 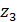 , получают:
, получают:  . Отсюда
. Отсюда 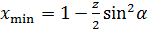 . С учётом формулы для
. С учётом формулы для  , получают
, получают 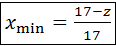 .
.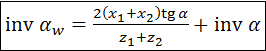 .
.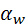 находят по таблице эвольвентной функции.
находят по таблице эвольвентной функции.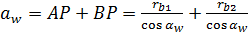 .
.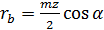 .
. 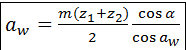 .
.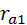 окружности вершин зубьев. Непосредственно из рис. 5.13 следует:
окружности вершин зубьев. Непосредственно из рис. 5.13 следует: 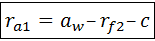 .
. принимают равным высоте
принимают равным высоте 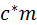 закруглённой части производящего контура, т. е. 0,25
закруглённой части производящего контура, т. е. 0,25 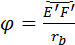 ,
, 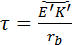 . Дуга
. Дуга 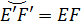 ,
,  . После подстановок
. После подстановок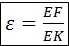 .
.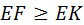 , т. е. активная линия зацепления длиннее шага колеса по той же линии.
, т. е. активная линия зацепления длиннее шага колеса по той же линии. , то в зацеплении постоянно находится только одна пара зубьев, если
, то в зацеплении постоянно находится только одна пара зубьев, если 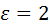 , то – две, и т. д. Если
, то – две, и т. д. Если 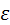 заключено между единицей и двойкой, то в зацеплении поочерёдно находится то одна, то две пары зубьев.
заключено между единицей и двойкой, то в зацеплении поочерёдно находится то одна, то две пары зубьев.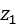 ,
, 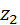 . Осями координат контура являются коэффициенты смещения
. Осями координат контура являются коэффициенты смещения 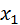 ,
,  . Коэффициенты смещения должны соответствовать любой точке, заключенной внутри контура или лежащей на его границе. Такой выбор коэффициентов гарантирует следующие четыре качества зацепления:
. Коэффициенты смещения должны соответствовать любой точке, заключенной внутри контура или лежащей на его границе. Такой выбор коэффициентов гарантирует следующие четыре качества зацепления: (незаострение);
(незаострение);


