Прямозубое эвольвентное зацепление
Похожие статьи вашей тематики
Боковые поверхности зубьев конических колёс формируют в принципе так же, как и цилиндрических. Разница лишь в том, что основные цилиндры заменяют основными конусами – B 1 и B 2 (рис. 5.19, а).
Рис. 5.19. Образование конического эвольвентного зацепления
Основания конусов лежат на сфере  , ограничивающей зацепление снаружи. По конусам перекатывается без скольжения плоскость , ограничивающей зацепление снаружи. По конусам перекатывается без скольжения плоскость  , несущая рисующую линию , несущая рисующую линию 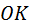 . В пространстве каждого из конусов точка . В пространстве каждого из конусов точка 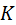 этой прямой описывает эвольвенты Э 1, Э 2, лежащие на сфере этой прямой описывает эвольвенты Э 1, Э 2, лежащие на сфере  . Прочие точки прямой . Прочие точки прямой 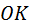 описывают эвольвенты, лежащие на сферах меньшего радиуса. Совокупность всех таких эвольвент образует боковые поверхности конического прямозубого эвольвентного зацепления. описывают эвольвенты, лежащие на сферах меньшего радиуса. Совокупность всех таких эвольвент образует боковые поверхности конического прямозубого эвольвентного зацепления.
Рисующая прямая 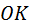 оказывается одновременно линией контакта зубьев. Точка оказывается одновременно линией контакта зубьев. Точка 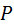 – полюс зацепления, прямая – полюс зацепления, прямая  – полюсная линия, по ней касаются друг друга аксоиды A 1, A 2, они же – начальные конусы. Дуга – полюсная линия, по ней касаются друг друга аксоиды A 1, A 2, они же – начальные конусы. Дуга 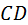 – линия зацепления, – линия зацепления, 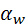 – угол зацепления, плоскость его отсчёта перпендикулярна межосевой плоскости – угол зацепления, плоскость его отсчёта перпендикулярна межосевой плоскости  . .
Передаточное отношение. Как и в плоском зацеплении, передаточное отношение определяют числа зубьев, а также радиусы основных и начальных окружностей. В коническом зацеплении передаточное отношение определяют также углы  , ,  начальных конусов (рис. 5.19, б): начальных конусов (рис. 5.19, б):
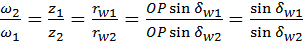 . .
Как правило, межосевой угол 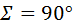 . При этом (рис. 5.21, в): . При этом (рис. 5.21, в):
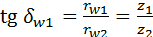 ; ; 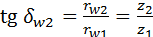 . .
Изготовление зацепления
Аналогом производящего реечного контура, известного по плоскому зацеплению, является при этом контур ПК, построенный на сфере (рис. 5.20, а).
При изготовлении зацепления без коррекции делительная линия ДЛ производящего контура лежит в плоскости так называемого большого круга, проходящего через центр сферы. Этот круг обкатывается по аксоидам (начальным конусам)  , , 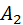 производимого зацепления и, следовательно, является ещё одним аксоидом – производимого зацепления и, следовательно, является ещё одним аксоидом –  (5.20, б). (5.20, б).

Рис. 5.20. Образование конического зацепления,
близкого к эвольвентному (октоидального)
Каждый производящий профиль лежит в плоскости своего большого круга. Если смотреть на плоскость этого круга с ребра, то профиль будет выглядеть прямолинейным. Таким образом, сферический производящий контур в некотором смысле прямобочный. Соединяя точки излома контура с центром сферы, получают плоское производящее колесо с плоскими боковыми сторонами.
Основные параметры сферического производящего контура такие же, как у плоского. В частности, угол профиля 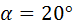 , шаг , шаг 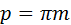 . Модуль по-прежнему выбирают из стандартного ряда предпочтительных чисел, при этом радиус . Модуль по-прежнему выбирают из стандартного ряда предпочтительных чисел, при этом радиус  сферы сферы  , ограничивающей зацепление снаружи, подчиняют уравнению , ограничивающей зацепление снаружи, подчиняют уравнению  . .
На первый взгляд, зацепление, произведённое прямобочным колесом, должно быть эвольвентным, но это не так. Производящая плоскость ПП (см. рис. 5.20, б), вмещающая производящий профиль, располагается наклонно (под углом 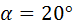 к вертикали) и составляет единое целое с аксоидом к вертикали) и составляет единое целое с аксоидом  . Аксоид . Аксоид  обкатывается по аксоидам обкатывается по аксоидам  и и 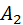 производимого зацепления П 1, П 2. Для простоты рисунка профиль П 2, а также аксоид производимого зацепления П 1, П 2. Для простоты рисунка профиль П 2, а также аксоид 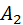 не показаны. не показаны.
Контактная линия 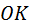 производящей и обеих производимых поверхностей есть линия пересечения производящей плоскости ПП и плоскости производящей и обеих производимых поверхностей есть линия пересечения производящей плоскости ПП и плоскости  , перпендикулярной ПП. Перпендикулярность вытекает из основной теоремы плоского зацепления: нормаль к профилям зубьев проходит через полюс зацепления. В роли нормали (перпендикуляра к , перпендикулярной ПП. Перпендикулярность вытекает из основной теоремы плоского зацепления: нормаль к профилям зубьев проходит через полюс зацепления. В роли нормали (перпендикуляра к 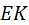 ) выступает здесь дуга ) выступает здесь дуга  . .
Нетрудно видеть, что по мере удаления точки 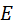 от от 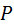 угол угол 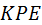 возрастает. Ввиду переменности угла возрастает. Ввиду переменности угла 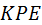 линия зацепления ЛЗ (см. рис. 5.20, а) не лежит в плоскости большого круга, как это имеет место в эвольвентном зацеплении, а имеет вид восьмёрки. Отсюда рассматриваемое зацепление называется октоидальным (от латинского octo – восемь). линия зацепления ЛЗ (см. рис. 5.20, а) не лежит в плоскости большого круга, как это имеет место в эвольвентном зацеплении, а имеет вид восьмёрки. Отсюда рассматриваемое зацепление называется октоидальным (от латинского octo – восемь).
Вблизи полюса, где реально взаимодействуют зубья, октоидальное зацепление практически не отличается от эвольвентного. Отсюда оно называется квазиэвольвентным. Приставка квази- означает почти. Октоидальное зацепление, как и эвольвентное, имеет постоянное передаточное отношение, но не сохраняет этого постоянства при изменении межосевого угла 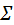 . .
Червячное зацепление
Зацепление состоит из червяка 1 и червячного колеса 2 (рис. 5.21, а). Червяк представляет собой однозаходный или многозаходный винт. Число заходов считается числом зубьев червяка. Центральная точка касания начальных поверхностей червячного зацепления располагается на линии кратчайшего расстояния между осями. В этой части червячное зацепление не отличается от винтового.
Рис. 5.21. Червячное зацепление: а, б – с цилиндрическим
червяком; в – с глобоидным
Чтобы повысить нагрузочную способность зацепления, начальные поверхности делают облегающими друг друга. Начальную поверхность червячного колеса делают тороидальной, а у червяка – цилиндрической или тоже тороидальной (рис. 5.21, б, в).
В первом случае касание начальных поверхностей происходит по линии, во втором – по поверхности. Червяк с тороидальной начальной поверхностью называется глобоидным, т. е. охватывающим. Охватывающая форма увеличивает количество зубьев, находящихся в зацеплении одновременно.
Другим средством, повышающим нагрузочную способность зацепления, является образование червячного колеса производящей поверхностью, совпадающей с поверхностью червяка. Производящая поверхность и производимое червячное колесо располагаются относительно друг друга так же, как в рабочем зацеплении, и вращаются со скоростями, обратными числам зубьев рабочего зацепления. При этом зубья станочного и рабочего зацеплений касаются друг друга по линии.
Теоретически форма поверхности червяка может быть любой. Но поскольку с ней должна совпадать физическая производящая поверхность, то на практике выбор поверхности червяка – это выбор существующего стандартного инструмента. Наибольшее распространение имеют червяки и инструменты (червячные фрезы) с архимедовой и эвольвентной винтовыми поверхностями. Первая образуется вращательным и поступательным движением прямой 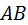 , пересекающей ось червяка (рис. 5.22, а), вторая – прямой , пересекающей ось червяка (рис. 5.22, а), вторая – прямой 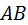 , смещённой на некоторое расстояние , смещённой на некоторое расстояние 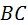 (рис. 5.22, в). (рис. 5.22, в).
В обоих случаях скорости  , ,  вращательного и поступательного движений постоянны. В случае б) прямая вращательного и поступательного движений постоянны. В случае б) прямая 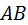 располагается в плоскости, касательной к цилиндру радиуса располагается в плоскости, касательной к цилиндру радиуса 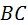 . Угол наклона . Угол наклона 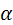 прямой прямой 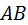 равен углу подъёма винтовой линии равен углу подъёма винтовой линии 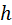 , описываемой точкой , описываемой точкой  на цилиндре на цилиндре 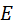 . Своё название поверхности получили за торцевые сечения. Первое является спиралью Архимеда (рис. 5.22, б), второе – эвольвентой окружности радиуса . Своё название поверхности получили за торцевые сечения. Первое является спиралью Архимеда (рис. 5.22, б), второе – эвольвентой окружности радиуса 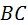 (рис. 5.22, г). (рис. 5.22, г).
Архимедова винтовая поверхность должна быть знакома читателю по резьбовым соединениям. Эвольвентная винтовая поверхность известна по косозубому зацеплению. Там она образовывалась прямой линией, принадлежащей гибкой нерастяжимой ленте, перематывающейся с одного цилиндра на другой. Названным объектам на данном рисунке соответствует прямая 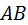 , которую можно считать принадлежащей ленте , которую можно считать принадлежащей ленте 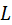 , наматывающейся на цилиндр , наматывающейся на цилиндр 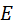 . Разница лишь в том, что у косозубого колеса угол . Разница лишь в том, что у косозубого колеса угол 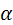 ближе к ближе к  °, а у червяка ближе к нулю. Таким образом, эвольвентный червяк – это сильно закрученное косозубое эвольвентное колесо с одним или несколькими зубьями. °, а у червяка ближе к нулю. Таким образом, эвольвентный червяк – это сильно закрученное косозубое эвольвентное колесо с одним или несколькими зубьями.
Если угол 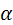 не равен углу подъёма винтовой линии, то в торцевом сечении получается удлинённая или укороченная эвольвента. Червяк с поверхностью, соответствующей этому случаю, называется конволютным. не равен углу подъёма винтовой линии, то в торцевом сечении получается удлинённая или укороченная эвольвента. Червяк с поверхностью, соответствующей этому случаю, называется конволютным.
Архимедова и эвольвентная поверхности линейчатые. Сечение первой прямолинейно в осевой плоскости, сечение второй прямолинейно в плоскости  . Несмотря на линейчатость, к архимедовой поверхности невозможно провести касательную плоскость. По этой причине становится невозможной обработка эвольвентного червяка плоскостью шлифовального круга. Эвольвентный и конволютный червяки лишены этого недостатка. . Несмотря на линейчатость, к архимедовой поверхности невозможно провести касательную плоскость. По этой причине становится невозможной обработка эвольвентного червяка плоскостью шлифовального круга. Эвольвентный и конволютный червяки лишены этого недостатка.
Рис. 5.22. Образование Архимедова – а и эвольвентного – в червяков
Образование зацепления производящей поверхностью, совпадающей с поверхностью одного из колёс, известно как второй способ Оливье. Первый способ состоит в том, что зацепление образуется от поверхности, не совпадающей ни с одним из колёс. Все зацепления, которые рассматривались до сих пор, т. е. до червячного, образовывались по первому способу.
Сложные зубчатые передачи
|



 , ограничивающей зацепление снаружи. По конусам перекатывается без скольжения плоскость
, ограничивающей зацепление снаружи. По конусам перекатывается без скольжения плоскость  , несущая рисующую линию
, несущая рисующую линию 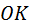 . В пространстве каждого из конусов точка
. В пространстве каждого из конусов точка 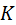 этой прямой описывает эвольвенты Э 1, Э 2, лежащие на сфере
этой прямой описывает эвольвенты Э 1, Э 2, лежащие на сфере  . Прочие точки прямой
. Прочие точки прямой 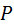 – полюс зацепления, прямая
– полюс зацепления, прямая  – полюсная линия, по ней касаются друг друга аксоиды A 1, A 2, они же – начальные конусы. Дуга
– полюсная линия, по ней касаются друг друга аксоиды A 1, A 2, они же – начальные конусы. Дуга 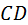 – линия зацепления,
– линия зацепления, 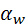 – угол зацепления, плоскость его отсчёта перпендикулярна межосевой плоскости
– угол зацепления, плоскость его отсчёта перпендикулярна межосевой плоскости  .
. ,
,  начальных конусов (рис. 5.19, б):
начальных конусов (рис. 5.19, б):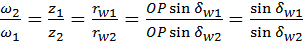 .
.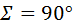 . При этом (рис. 5.21, в):
. При этом (рис. 5.21, в):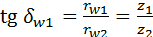 ;
; 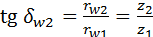 .
. ,
, 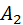 производимого зацепления и, следовательно, является ещё одним аксоидом –
производимого зацепления и, следовательно, является ещё одним аксоидом –  (5.20, б).
(5.20, б).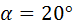 , шаг
, шаг 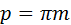 . Модуль по-прежнему выбирают из стандартного ряда предпочтительных чисел, при этом радиус
. Модуль по-прежнему выбирают из стандартного ряда предпочтительных чисел, при этом радиус  сферы
сферы  .
. , перпендикулярной ПП. Перпендикулярность вытекает из основной теоремы плоского зацепления: нормаль к профилям зубьев проходит через полюс зацепления. В роли нормали (перпендикуляра к
, перпендикулярной ПП. Перпендикулярность вытекает из основной теоремы плоского зацепления: нормаль к профилям зубьев проходит через полюс зацепления. В роли нормали (перпендикуляра к 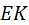 ) выступает здесь дуга
) выступает здесь дуга  .
.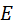 от
от 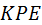 возрастает. Ввиду переменности угла
возрастает. Ввиду переменности угла 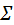 .
.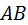 , пересекающей ось червяка (рис. 5.22, а), вторая – прямой
, пересекающей ось червяка (рис. 5.22, а), вторая – прямой 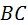 (рис. 5.22, в).
(рис. 5.22, в). ,
,  вращательного и поступательного движений постоянны. В случае б) прямая
вращательного и поступательного движений постоянны. В случае б) прямая 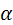 прямой
прямой 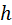 , описываемой точкой
, описываемой точкой  на цилиндре
на цилиндре 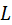 , наматывающейся на цилиндр
, наматывающейся на цилиндр  °, а у червяка ближе к нулю. Таким образом, эвольвентный червяк – это сильно закрученное косозубое эвольвентное колесо с одним или несколькими зубьями.
°, а у червяка ближе к нулю. Таким образом, эвольвентный червяк – это сильно закрученное косозубое эвольвентное колесо с одним или несколькими зубьями. . Несмотря на линейчатость, к архимедовой поверхности невозможно провести касательную плоскость. По этой причине становится невозможной обработка эвольвентного червяка плоскостью шлифовального круга. Эвольвентный и конволютный червяки лишены этого недостатка.
. Несмотря на линейчатость, к архимедовой поверхности невозможно провести касательную плоскость. По этой причине становится невозможной обработка эвольвентного червяка плоскостью шлифовального круга. Эвольвентный и конволютный червяки лишены этого недостатка.


