
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы и свойства эвольвентного зацепленияСодержание книги
Поиск на нашем сайте
Э л е м е н т ы з а ц е п л е н и я п а р ы к о л ё с. Отметим прежде всего, что здесь рассматриваются те элементы, которые имеются именно в зацеплении колёс, а у отдельного колеса их нет (рис. 8.13). К этим элементам относятся следующие.
Межосевое расстояние Угол зацепления Сопряжённые (или парные) точки – это точки профилей зубьев, которыми они касаются друг друга на линии зацепления. Радиальный зазор – это расстояние c на межосевой линии между точками пересечения её с окружностью вершин одного колеса и впадин другого колеса. Величина радиального зазора равна С в о й с т в а э в о л ь в е н т н о г о з а ц е п л е н и я. 1. Передаточное отношение постоянно в любой фазе зацепления, так как оно может быть выражено через радиусы основных окружностей. Для доказательства используем подобные прямоугольные треугольники (рис. 8.13)
2. Передаточное отношение не зависит от изменения межосевого расстояния 3. Правильное зацепление эвольвентных профилей происходит только в пределах линии зацепления N1N2, так как только в этих пределах контактирующие эвольвентные профили имеют общую нормаль. 4. Эвольвентные колёса одного модуля имеют полную взаимозаменяемость, то есть могут составить правильное зацепление.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.61.142 (0.011 с.) |


 – это расстояние между центрами колёс O 1 и O 2. Полюс зацепления П – это точка касания центроидных окружностей колёс с радиусами
– это расстояние между центрами колёс O 1 и O 2. Полюс зацепления П – это точка касания центроидных окружностей колёс с радиусами  и
и  , которые в эвольвентном зацеплении называются начальными окружностями. Теоретическая линия зацепления N 1 N 2 – это геометрическое место точек мгновенного касания профилей зубьев, отмеченное на неподвижной плоскости. Процесс передачи движения происходит таким образом, что профили одной пары зубьев на протяжении некоторого времени касаются друг друга, то есть имеют общую нормаль. На основании первого свойства эвольвенты нормаль к ней является касательной к основной окружности, а для двух касающихся друг друга профилей является касательной к обеим основным окружностям. Поэтому для данных профилей контактная нормаль является единственной и лежит на общей касательной к основным окружностям, образуя, таким образом, прямолинейную линию зацепления. С учётом геометрических размеров конкретных колёс линия зацепления используется для передачи движения только в пределах зоны, заключённой между точками её пересечения с окружностями вершин (рис. 8.13). Эта зона называется активной линией зацепления. Её границы на рисунке отмечены точками H 1 и H 2, и она проведена жирной линией.
, которые в эвольвентном зацеплении называются начальными окружностями. Теоретическая линия зацепления N 1 N 2 – это геометрическое место точек мгновенного касания профилей зубьев, отмеченное на неподвижной плоскости. Процесс передачи движения происходит таким образом, что профили одной пары зубьев на протяжении некоторого времени касаются друг друга, то есть имеют общую нормаль. На основании первого свойства эвольвенты нормаль к ней является касательной к основной окружности, а для двух касающихся друг друга профилей является касательной к обеим основным окружностям. Поэтому для данных профилей контактная нормаль является единственной и лежит на общей касательной к основным окружностям, образуя, таким образом, прямолинейную линию зацепления. С учётом геометрических размеров конкретных колёс линия зацепления используется для передачи движения только в пределах зоны, заключённой между точками её пересечения с окружностями вершин (рис. 8.13). Эта зона называется активной линией зацепления. Её границы на рисунке отмечены точками H 1 и H 2, и она проведена жирной линией. – это угол между линией зацепления и общей касательной к начальным окружностям, проведённой через полюс зацепления П.
– это угол между линией зацепления и общей касательной к начальным окружностям, проведённой через полюс зацепления П.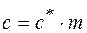 , где
, где 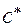 – это коэффициент радиального зазора, в соответствии со стандартом равный 0,25.
– это коэффициент радиального зазора, в соответствии со стандартом равный 0,25. и
и  и запишем цепочку равенств:
и запишем цепочку равенств:  .
.


