
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование пуска машины при силах – функциях скоростейСодержание книги
Поиск на нашем сайте
Этот случай является типичным для машин ротативного типа, имеющих
Уравнение динамики для данных условий запишется так:
или, после выполнения действий в правой части,
Множители в скобках в правой части уравнения одинаковы, поэтому можно записать
Поскольку
В качестве примера воспользуемся полученным уравнением для анализа пуска машины с конкретными данными. Пусть в момент пуска величина избыточного момента
Программа составляется согласно методике, разработанной для решения обыкновенных дифференциальных уравнений (ОДУ) в указанном пакете. Сначала вводится ключевое слово Given, за которым следуют: решаемое ОДУ, начальное условие, согласно задаче Коши, и затем – встроенная функция Odesolve с указанием аргумента (в данном случае t) и принятого конечного значения T его изменения. Результат решения представляется в виде графика искомой функции Исследование устойчивости
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.1.58 (0.01 с.) |

 , с приводом от электродвигателя. Движущий момент определяется механической характеристикой
, с приводом от электродвигателя. Движущий момент определяется механической характеристикой  , а момент сил сопротивления часто является постоянной величиной (вентиляторы, мешалки, центрифуги, осевые или центробежные насосы и т. д.).
, а момент сил сопротивления часто является постоянной величиной (вентиляторы, мешалки, центрифуги, осевые или центробежные насосы и т. д.). Предположим, что двигателем является электромотор постоянного тока, характеристика которого приблизительно прямолинейна:
Предположим, что двигателем является электромотор постоянного тока, характеристика которого приблизительно прямолинейна:  , где
, где  – пусковой момент (рис. 6.11). Приведённые к валу мотора силы сопротивления дают постоянный приведённый момент
– пусковой момент (рис. 6.11). Приведённые к валу мотора силы сопротивления дают постоянный приведённый момент  . Приведённый момент инерции также постоянен, то есть
. Приведённый момент инерции также постоянен, то есть  . Когда машина достигнет установившегося режима движения, скорость её вала станет
. Когда машина достигнет установившегося режима движения, скорость её вала станет  . Это произойдёт при равенстве моментов
. Это произойдёт при равенстве моментов  в точке K, в которой пересекаются характеристики
в точке K, в которой пересекаются характеристики  и
и  . Из этого равенства определится коэффициент b, то есть
. Из этого равенства определится коэффициент b, то есть  .
.


 , т. к. это движущий момент, а
, т. к. это движущий момент, а  , так как это момент сопротивления, то разность моментов в скобках уравнения, по существу, представляет их сумму с учётом знаков и является избыточным моментом в самом начале пуска, то есть
, так как это момент сопротивления, то разность моментов в скобках уравнения, по существу, представляет их сумму с учётом знаков и является избыточным моментом в самом начале пуска, то есть  Таким образом, окончательно дифференциальное уравнение движения машины запишется так
Таким образом, окончательно дифференциальное уравнение движения машины запишется так
 , приведённый момент инерции
, приведённый момент инерции  , номинальная угловая скорость в конце пуска
, номинальная угловая скорость в конце пуска 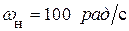 . Под номинальной понимается угловая скорость установившегося движения. Для решения дифференциального уравнения необходимо задаться также временем пуска, поэтому примем его произвольное значение
. Под номинальной понимается угловая скорость установившегося движения. Для решения дифференциального уравнения необходимо задаться также временем пуска, поэтому примем его произвольное значение  . Эти исходные данные приведены в программе решения с помощью математического пакета MathCAD (Лис-
. Эти исходные данные приведены в программе решения с помощью математического пакета MathCAD (Лис-
 и таблицы числовых значений угловой скорости для выбранного количества точек в пределах изменения времени
и таблицы числовых значений угловой скорости для выбранного количества точек в пределах изменения времени  . Из графика и таблицы видно, что процесс пуска заканчивается приблизительно к девятой секунде после начала, так как в дальнейшем изменение скорости
. Из графика и таблицы видно, что процесс пуска заканчивается приблизительно к девятой секунде после начала, так как в дальнейшем изменение скорости  практически отсутствует. Это подтверждается и графиком функции углового ускорения
практически отсутствует. Это подтверждается и графиком функции углового ускорения  , который выведен также в качестве результата анализа процесса пуска. На этом графике видно, что после точки
, который выведен также в качестве результата анализа процесса пуска. На этом графике видно, что после точки  угловое ускорение практически равно нулю. Так что можно принять
угловое ускорение практически равно нулю. Так что можно принять  К этому времени угловая скорость машины не достигает своего номинального значения всего на один процент.
К этому времени угловая скорость машины не достигает своего номинального значения всего на один процент.


