
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вспомогательные задачи динамики машинСодержание книги
Поиск на нашем сайте
На схеме рис. 6.1 обозначены: П р и в е д ё н н ы й м о м е н т и н е р ц и и м е х а н и з м а. Приведённым моментом инерции механизма называется момент инерции условного диска, вращающегося с угловой скоростью ведущего звена, которым заменяется реальный механизм и который обладает кинетической энергией, равной сумме кинетических энергий всех звеньев механизма. Кинетическая энергия условного диска Кинетическая энергия звена, совершающего поступательное движение, Кинетическая энергия звена, совершающего вращательное движение, Кинетическая энергия звена в плоскопараллельном движении
Подставив сюда записанные выше выражения кинетических энергий и решая затем полученное равенство относительно
Как видно из этой формулы, приведённый момент инерции зависит от структуры механизма, от массовых характеристик звеньев, от положения механизма и не зависит от угловой скорости ведущего звена. Некоторые механизмы имеют постоянное значение приведённого момента инерции. Машины, в основе которых механизмы с
П р и в е д ё н н ы й м о м е н т с и л с о п р о т и в л е н и я. Приведённым моментом сил сопротивления называется момент, приложенный к звену приведения (например, кривошипу), мгновенная мощность которого равна сумме мгновенных мощностей всех сил сопротивления, действующих в механизме. Мгновенная мощность приведённого момента сопротивления
Если среди сил сопротивления имеются моменты, то их можно представить в виде пар сил с плечами, равными длинам соответствующих звеньев. Замечание. Если во всех математических выражениях заменить силы сопротивления движущими силами, то в результате получится приведённый момент движущих сил
Зависимость приведённых моментов сил от угла поворота ведущего звена, его скорости или времени называется механической характеристикой машины.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.36.138 (0.006 с.) |

 Д и н а м и ч е с к а я м о д е л ь м а ш и н ы. В связи с необходимостью упрощения расчётной схемы и большей наглядности, а также сокращения расчётов реальную машину заменяют её моделью, сохраняющей те свойства машины, которые изучаются на данном этапе исследования. Такая модель представляет собой некоторый условный диск, вращающийся с кривошипом как одно целое, то есть с его угловой скоростью (рис. 6.1), обладающий так называемым приведённым моментом инерции. На этой основе кривошип или другое ведущее звено, с которым связан условный диск, называется звеном приведения. На диск действуют приведённый момент движущих сил, направленный в сторону вращения, и приведённый момент сил сопротивления, направленный навстречу вращению.
Д и н а м и ч е с к а я м о д е л ь м а ш и н ы. В связи с необходимостью упрощения расчётной схемы и большей наглядности, а также сокращения расчётов реальную машину заменяют её моделью, сохраняющей те свойства машины, которые изучаются на данном этапе исследования. Такая модель представляет собой некоторый условный диск, вращающийся с кривошипом как одно целое, то есть с его угловой скоростью (рис. 6.1), обладающий так называемым приведённым моментом инерции. На этой основе кривошип или другое ведущее звено, с которым связан условный диск, называется звеном приведения. На диск действуют приведённый момент движущих сил, направленный в сторону вращения, и приведённый момент сил сопротивления, направленный навстречу вращению.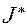 – приведённый момент инерции механизма,
– приведённый момент инерции механизма, 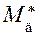 – приведённый момент движущих сил и
– приведённый момент движущих сил и 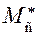 – приведённый момент сил сопротивления.
– приведённый момент сил сопротивления.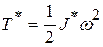 , где
, где 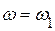 , то есть угловая скорость звена приведения, равная угловой скорости ведущего звена (чаще всего, но не обязательно, кривошипа).
, то есть угловая скорость звена приведения, равная угловой скорости ведущего звена (чаще всего, но не обязательно, кривошипа).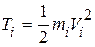 , где
, где 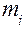 – масса звена;
– масса звена; 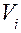 – скорость звена.
– скорость звена.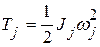 , где
, где 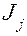 – момент инерции звена;
– момент инерции звена; 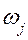 – угловая скорость звена.
– угловая скорость звена.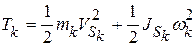 , где
, где 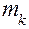 – масса звена;
– масса звена; 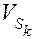 – скорость центра масс звена,
– скорость центра масс звена, 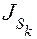 – момент инерции звена относительно его центра масс;
– момент инерции звена относительно его центра масс; 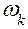 – угловая скорость звена. Согласно определению имеем
– угловая скорость звена. Согласно определению имеем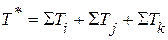 .
.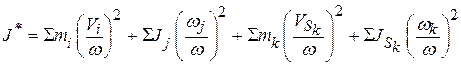 .
.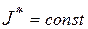 , называются ротативными.
, называются ротативными.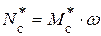 . Мгновенная мощность
. Мгновенная мощность 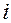 -й силы сопротивления
-й силы сопротивления 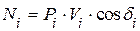 . Согласно определению
. Согласно определению 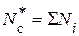 , поэтому, подставив сюда соответствующие выражения, получаем
, поэтому, подставив сюда соответствующие выражения, получаем 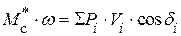 , откуда
, откуда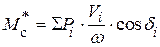 .
. .
.


