
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности зацепления конических колёсСодержание книги
Поиск на нашем сайте
Передача движения с помощью высшей пары может осуществляться не только между параллельными осями звеньев, но также и между пересекающимися осями. В этом случае аналогами центроидных окружностей, а точнее – аксоидных цилиндров (от англ. слова axis – ось) передач с цилиндрическими колёсами здесь являются конусы, имеющие общую вершину и перекатывающиеся друг по другу без скольжения. Эти конусы называются также аксоидами, так как каждый из них является геометрическим местом вращения одного колеса относительно другого. Зубья колёс располагаются на конусах, в результате чего и возникло название конической передачи, или передачи коническими колёсами (рис. 8.33).
В связи со сферическим характером движения конусов профилирование зубьев колёс должно производиться на сфере. Однако из-за сложности и громоздкости расчётов, мирясь с некоторой погрешностью, сферу заменяют дополнительными конусами (рис. 8.35). Дополнительные конусы развёртываются на плоскость, образуя секторы, на которых располагаются зубья
Установим связь между числами зубьев эквивалентных цилиндрических колёс и числами зубьев конических колёс. Из рис 8. 35 видим, что половины углов конусов могут быть выражены таким образом:
откуда
Внешний окружной модуль
Модуль конических колёс является переменной величиной, уменьшаясь от периферии к точке O, принимая минимальное значение на том основании усечённого конуса, которое ближе расположено к точке O. Передаточное отношение передачи эквивалентными цилиндрическими колёсами определяется отношением соответствующих чисел зубьев, что приводит к следующему:
Минимальное количество зубьев, нарезаемых без подреза, у конического колеса меньше, чем у цилиндрического, так как если полное эквивалентное колесо имеет
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.83.68 (0.009 с.) |


 В данной передаче колёса совершают сферическое движение по отношению друг к другу, так как, если остановить одно из колёс, а другое перекатывать по нему, то можно увидеть, что точки подвиж-ного колеса описывают кривые, лежащие на сферах с центром в точке O, совпадающей с общей вершиной конусов (рис. 8.34). Указанные конусы называются начальными. Половинные углы конусов при вершине O обозна-чаются
В данной передаче колёса совершают сферическое движение по отношению друг к другу, так как, если остановить одно из колёс, а другое перекатывать по нему, то можно увидеть, что точки подвиж-ного колеса описывают кривые, лежащие на сферах с центром в точке O, совпадающей с общей вершиной конусов (рис. 8.34). Указанные конусы называются начальными. Половинные углы конусов при вершине O обозна-чаются  – первого колеса и
– первого колеса и  – второго колеса. Угол между осями конусов обозначен
– второго колеса. Угол между осями конусов обозначен  , причём
, причём  . Точка касания оснований конусов, аналогичная полюсу зацепления в цилиндрической передаче, обозначена П. При условии, что окружности оснований конусов катятся друг по другу без скольжения, и в точке П их скорости одинаковы, имеем равенство
. Точка касания оснований конусов, аналогичная полюсу зацепления в цилиндрической передаче, обозначена П. При условии, что окружности оснований конусов катятся друг по другу без скольжения, и в точке П их скорости одинаковы, имеем равенство 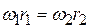 , из которого ясно:
, из которого ясно: .
. – первого колеса и
– первого колеса и 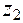 – второго колеса. Развёртки дополнительных конусов с зубьями на плоскость называют эквивалентными цилиндрическими колёсами. Количество зубьев на секторах равно количеству зубьев на конусах. Однако, если заполнить развёртки секторов зубьями до полного круга, то количество зубьев на круге разместится больше, чем было на секторе. Так что полные эквивалентные цилиндрические колёса имеют числа зубьев
– второго колеса. Развёртки дополнительных конусов с зубьями на плоскость называют эквивалентными цилиндрическими колёсами. Количество зубьев на секторах равно количеству зубьев на конусах. Однако, если заполнить развёртки секторов зубьями до полного круга, то количество зубьев на круге разместится больше, чем было на секторе. Так что полные эквивалентные цилиндрические колёса имеют числа зубьев 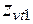 – первое колесо и
– первое колесо и  – второе колесо, которые больше чем
– второе колесо, которые больше чем 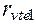 и
и 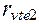 соответственно.
соответственно.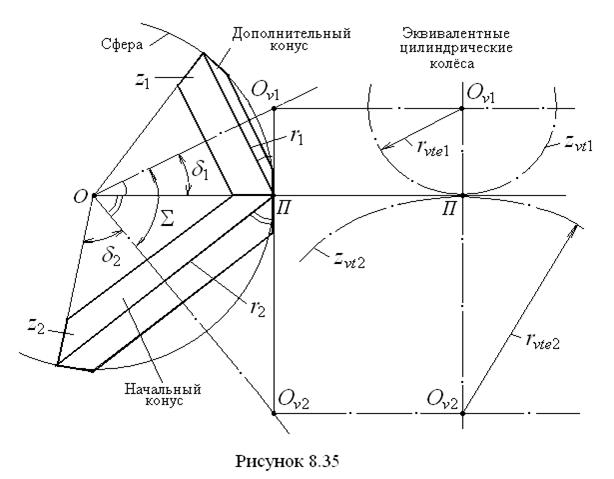
 и
и  ,
, ,
,  .
. , соответствующий шагу конического колеса и шагу эквивалентной цилиндрической передачи, один и тот же. Поэтому, поделив левые и правые части в последней паре формул на
, соответствующий шагу конического колеса и шагу эквивалентной цилиндрической передачи, один и тот же. Поэтому, поделив левые и правые части в последней паре формул на 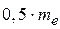 , получаем
, получаем ,
,  .
.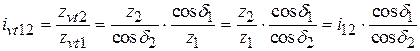 .
.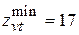 , то для получения конического колеса его необходимо сократить, чтобы образовался сектор, а затем этот сектор свернуть в конус. При этом получается
, то для получения конического колеса его необходимо сократить, чтобы образовался сектор, а затем этот сектор свернуть в конус. При этом получается  , откуда ясно, что
, откуда ясно, что 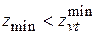 .
.


