
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт геометрических размеров зубчатых колёсСодержание книги
Поиск на нашем сайте
Исходными данными для расчёта размеров служат числа зубьев колёс У г о л з а ц е п л е н и я. Формулу для определения угла зацепления приведём здесь без вывода из-за его громоздкости
Из этой формулы, в частности, видно, что в нулевой передаче Р а д и у с ы н а ч а л ь н ы х о к р у ж н о с т е й и м е ж о с е в о е р а с- с т о я н и е. Для вывода формул обратимся к рис. 8.26 на котором показаны необходимые элементы зацепления. Линия зацепления N 1 N 2 образует угол зацепления
Как видно из рисунка, межосевое расстояние равно сумме радиусов начальных окружностей, то есть
Произведение первых двух сомножителей в этой формуле называется делительным межосевым расстоянием. Оно имеет место, когда передача изготавливается нулевой, то есть когда суммарный коэффициент смещения равен нулю. При этом Р а д и у с ы о к р у ж н о с т е й в п а д и н. При образовании нулевого колеса его центроидой, как и всегда, является делительная окружность (рис. 8.27), а центроидой инструмента служит его делительная прямая (на рисунке профиль инструмента и его делительная прямая и прямая вершин показаны тонкими линиями). Поэтому радиус
На рис. 8.27 расположение смещённого инструмента по отношению к нарезаемому колесу изображено жирными линиями.
Р а д и у с ы о к р у ж н о с т е й в е р ш и н. Расчёт радиусов окружностей вершин понятен из рис. 8.28, где представлены элементы зацепления, связанные с этим расчётом. Непосредственно из рисунка видно, что радиус окружности вершин первого колеса
радиус окружности вершин второго колеса
Т о л щ и н а з у б а п о д е л и т е л ь н о й о к р у ж н о с т и. Толщина зуба колеса по делительной окружности определяется шириной впадины инструментальной рейки по станочно-начальной прямой (рис. 8.29), которая при изготовлении колеса перекатывается по его делительной окружности без скольжения.
или в окончательном виде, после несложного преобразования
Во всех формулах расчёта геометрических размеров зубчатых колёс коэффициенты смещения необходимо подставлять с их знаками.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.231 (0.01 с.) |

 и
и  , модуль колёс
, модуль колёс  , угол профиля исходного контура
, угол профиля исходного контура  , коэффициенты смещения
, коэффициенты смещения 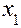 и
и  , коэффициент высоты головки зуба
, коэффициент высоты головки зуба  и коэффициент радиального зазора
и коэффициент радиального зазора 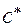 .
. .
.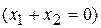 угол зацепления
угол зацепления 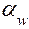 равен углу профиля инструмента
равен углу профиля инструмента 
 , в отрицательной передаче наоборот, то есть
, в отрицательной передаче наоборот, то есть  и соответственно
и соответственно  .
. с общей касательной к начальным окружностям радиусов
с общей касательной к начальным окружностям радиусов  и
и  , касающимся друг друга в полюсе Π. Опустив перпендикуляры из центров колёс O 1 и O 2 на линию зацепления, получаем два прямоугольных треугольника N 1 O 1 П и N 2 O 2 П с углами при вершинах O 1 и O 2, равными
, касающимся друг друга в полюсе Π. Опустив перпендикуляры из центров колёс O 1 и O 2 на линию зацепления, получаем два прямоугольных треугольника N 1 O 1 П и N 2 O 2 П с углами при вершинах O 1 и O 2, равными  , из треугольника N 2 O 2 П –
, из треугольника N 2 O 2 П –  . Так как имеют место равенства
. Так как имеют место равенства  ,
, 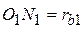 ,
,  и
и 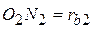 , а также
, а также  ,
,  , то получаем
, то получаем 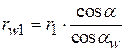 и
и  . Вместо радиусов делительных окружностей
. Вместо радиусов делительных окружностей  и
и  в эти формулы можно вставить их выражения, записанные ранее, тогда
в эти формулы можно вставить их выражения, записанные ранее, тогда
 ,
,  .
. , поэтому
, поэтому .
. и косинусы сокращаются.
и косинусы сокращаются. окружности впадин нулевого колеса равен разности
окружности впадин нулевого колеса равен разности  . При смещении инструмента на величину
. При смещении инструмента на величину  радиус окружности впадин увеличивается на эту же величину и приобретает значение
радиус окружности впадин увеличивается на эту же величину и приобретает значение .
.

 ,
, .
. Размер s толщины зуба складывается из ширины
Размер s толщины зуба складывается из ширины  впадины инструментальной рейки по её делительной прямой и двух катетов прямоугольных треу-
впадины инструментальной рейки по её делительной прямой и двух катетов прямоугольных треу- . С учётом этих соображений толщину зуба s можно выразить так
. С учётом этих соображений толщину зуба s можно выразить так ,
, .
.


