В механизме с плоским толкателем

 

В кулачковом механизме с плоским толкателем угол давления равен нулю во всех положениях, если ось толкателя перпендикулярна тарелке. В случае, если ось не перпендикулярна тарелке, то угол давления не равен нулю, но остаётся постоянным во всех положениях механизма. Поэтому для определения радиуса основной окружности кулачка необходимо выполнить другое условие, которое требуется для нормальной работы механизма. Таким условием является условие выпуклости профиля. Оно заключается в том, что во всех своих точках профиль кулачка должен быть выпуклым и не иметь провалов (рис. 9.16), так как плоская тарелка толкателя не сможет огибать провал (вогнутость) профиля, и закон движения толкателя в зоне провала не может быть реализован. На рисунке цифрами отмечены последовательные положения толкателя и штриховкой показан участок профиля кулачка, недоступный для контакта с толкателем. Чтобы такого явления не происходило, необходимо спроектировать профиль кулачка таким образом, чтобы на нём не было вогнутостей.

На форму профиля кулачка можно влиять радиусом основной окружности. Посмотрим, как связана геометрия профиля с радиусом . Возьмём кулачковый механизм с плоским толкателем (рис. 9.17). В данном положении механизма тарелка толкателя касается профиля кулачка в точке K. Определим в данной точке радиус кривизны профиля . Для этого проведём нормаль n – n к про-филю и найдём на ней центр кривизны C. Как видно из рисунка, радиус кривизны равен сумме . Согласно условию выпуклости профиля необходимо , то есть .

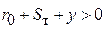Чтобы определить неизвестную координату центра кривизны C, обратимся к подобию треугольника OCD и треугольника ускорений, построенных из точки C. Из этого подобия запишем , откуда , где – ускорение толкателя, – ускорение точки C. Точка C принадлежит кулачку, вращающемуся с постоянной угловой скоростью . Поэтому её ускорение состоит только из нормальной составляющей . С учётом этого имеем . Но данное отношение представляет собой аналог ускорения толкателя . Тогда условие выпуклости запишется так: .

Перенесём аналог ускорения в правую часть неравенства и поделим всё выражение на : .

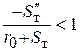Для дальнейшего заменим единицу , то есть .

Последнее неравенство позволяет определить , если представить его в форме графических построений. Выберем систему координат (рис. 9.18), по оси абсцисс которой отложим аналог ускорения , а по оси ординат – перемещение толкателя (масштабы по осям координат должны быть одинаковы), исключив параметр из предварительно найденных зависимостей и . Затем к отрицательной части диаграммы необходимо провести касательную под углом 45º до пересечения с осью . Так как левая часть неравенства меньше чем , то центр кулачка необходимо принять на 7…10 мм ниже точки пересечения касательной с осью ординат. Расстояние от этого центра до начала координат будет равно радиусу . Если радиус взять от точки пересечения касательной с осью ординат, то это соответствовало бы знаку равенства вместо знака неравенства.